Задача № 1

Условие.

По территориям Южного федерального округа приводятся данные за 2006 год:

Территории федерального округа	Валовой региональный продукт, млрд руб., Y	Кредиты, предоставленные предприятиям, организациям, банкам и физическим лицам, млн руб., X
1. Республика Адыгея	5,1	60,3
2. Республика Дагестан	13,0	469,5
3. Республика Ингушетия	2,0	10,5
4. Кабардино-Балкарская Республика	10,5	81,7
5. Республика Калмыкия	2,1	46,4
6. Карачаево-Черкесская Республика	4,3	96,4
7. Республика Северная Осетия – Алания	7,6	356,5
8. Краснодарский край1)	109,1	2463,5
9. Ставропольский край	43,4	278,6
10. Астраханская обл.	18,9	321,9
11. Волгоградская обл.	50,0	782,9
12. Ростовская обл. 1)	69,0	1914,0
Итого, 	156,9	2504,7
Средняя	15,69	250,47
Среднее квадратическое отклонение, 	16,337	231,56
Дисперсия, D	266,89	53620,74

¹⁾ Предварительный анализ исходных данных выявил наличие двух территорий с аномальными значениями признаков. Эти территории должны быть исключены из дальнейшего анализа.

Задание:

1. Расположите территории по возрастанию фактора X. Сформулируйте рабочую гипотезу о возможной связи Y и X.

2. Постройте поле корреляции и сформулируйте гипотезу о возможной форме и направлении связи.

3. Рассчитайте параметры а₁ и а₀ парной линейной функции .

4. Оцените тесноту связи с помощью показателей корреляции (r_yx ) и детерминации (r²_yx), проанализируйте их значения.

5.Надёжность уравнений в целом оцените через F -критерий Фишера для уровня значимости =0,05.

6. По уравнению регрессии рассчитайте теоретические значения результата ( ), по ним постройте теоретическую линию регрессии и определите среднюю ошибку аппроксимации - ε'_ср., оцените её величину.

7. Рассчитайте прогнозное значение результата , если прогнозное значение фактора ( ) составит 1,037 от среднего уровня ( ).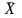

8. Рассчитайте интегральную и предельную ошибки прогноза (для =0,05), определите доверительный интервал прогноза ( ; ), а также диапазон верхней и нижней границ доверительного интервала ( ), оцените точность выполненного прогноза.

Решение.

1.

10,5	2
46,4	2,1
60,3	5,1
81,7	10,5
96,4	4,3
278,6	43,4
321,9	18,9
356,5	7,6
469,5	13
782,9	50
1914	69
2463,5	109,1

2.

На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.

3.

Линейное уравнение регрессии имеет вид y = bx + a a•n + b∑x = ∑y a∑x + b∑x² = ∑y•x 10a + 2504.7 b = 156.9 2504.7 a + 1163559.63 b = 67831.39 -2504.7a -627352.21 b = -39298.74 2504.7 a + 1163559.63 b = 67831.39 536207.42 b = 28532.65 b = 0.05321 10a + 2504.7 b = 156.9 10a + 2504.7 • 0.05321 = 156.9 10a = 23.62 a = 2.362 Получаем эмпирические коэффициенты регрессии: b = 0.05321, a = 2.362 Уравнение регрессии (эмпирическое уравнение регрессии): y = 0.05321 x + 2.362 Для расчета параметров регрессии построим расчетную таблицу (табл. 1)

x	y	x2	y2	x • y
10.5	2	110.25	4	21
46.4	2.1	2152.96	4.41	97.44
60.3	5.1	3636.09	26.01	307.53
81.7	10.5	6674.89	110.25	857.85
96.4	4.3	9292.96	18.49	414.52
278.6	43.4	77617.96	1883.56	12091.24
321.9	18.9	103619.61	357.21	6083.91
356.5	7.6	127092.25	57.76	2709.4
469.5	13	220430.25	169	6103.5
782.9	50	612932.41	2500	39145
2504.7	156.9	1163559.63	5130.69	67831.39

Параметры уравнения регрессии. Выборочные средние. Выборочные дисперсии: Среднеквадратическое отклонение Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно: 4.

Коэффициент корреляции Ковариация. Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле: Линейный коэффициент корреляции принимает значения от –1 до +1. Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока: 0.1 < r_xy < 0.3: слабая; 0.3 < r_xy < 0.5: умеренная; 0.5 < r_xy < 0.7: заметная; 0.7 < r_xy < 0.9: высокая; 0.9 < r_xy < 1: весьма высокая; В нашем примере связь между признаком Y фактором X высокая и прямая. Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b:

Коэффициент детерминации. R²= 0.754² = 0.5689 т.е. в 56.89 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - средняя. Остальные 43.11 % изменения Y объясняются факторами, не учтенными в модели (а также ошибками спецификации).

5.

F-статистика. Критерий Фишера. Табличное значение критерия со степенями свободы k₁=1 и k₂=8, F_табл = 5.32 Отметим значения на числовой оси.

Принятие H0	Отклонение H0, принятие H1
95%	5%
5.32	10.56

Поскольку фактическое значение F > F_табл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).

6.

Линейное уравнение регрессии имеет вид y = 0.0532 x + 2.36 Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент регрессии b = 0.0532 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 0.0532. Коэффициент a = 2.36 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями. Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо. Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения. Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь прямая. Ошибка аппроксимации. В среднем, расчетные значения отклоняются от фактических на 66.22%. Поскольку ошибка больше 7%, то данное уравнение не желательно использовать в качестве регрессии.

7,8

Доверительные интервалы для зависимой переменной. Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bx_p ± ε) где t_крит (n-m-1;α/2) = (8;0.025) = 2.306 Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X_p = 1.037 Вычислим ошибку прогноза для уравнения y = bx + a y(1.037) = 0.0532*1.037 + 2.362 = 2.417 2.417 ± 12.854 (-10.44;15.27) С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов. Вычислим ошибку прогноза для уравнения y = bx + a + ε (-28.08;32.91) Индивидуальные доверительные интервалы для Y при данном значении X. (a + bx_i ± ε) где t_крит (n-m-1;α/2) = (8;0.025) = 2.306

xi	y = 2.36 + 0.0532xi	εi	ymin = y - εi	ymax = y + εi
10.5	2.92	30.39	-27.47	33.31
46.4	4.83	30.01	-25.18	34.84
60.3	5.57	29.88	-24.31	35.45
81.7	6.71	29.7	-22.99	36.41
96.4	7.49	29.58	-22.09	37.08
278.6	17.19	29.03	-11.84	46.21
321.9	19.49	29.13	-9.64	48.62
356.5	21.33	29.28	-7.95	50.61
469.5	27.35	30.16	-2.82	57.51

С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.