
- •§2. Ортогональные системы функций.
- •§3. Интегралы от некоторых тригонометрических функций (вспомогательные интегралы).
- •§4. Ряд Фурье 2π-периодической функции.
- •§5. Достаточные признаки разложимости функции в ряд Фурье. Условие Дирихле.
- •§6. Ряд Фурье чётных и нечётных функций с .
- •§7. Ряд Фурье функции с произвольным периодом.
Гл. Ряды Фурье. Интеграл Фурье.
§.1. Периодические функции и их свойства.
Пусть f(x) функция определена а всей числовой оси
Df1. Число Т называется периодом f(x) если для ∀x∈R справедливо равенство
f(x+T) =f(x), T>0
Df2. Функция имеющая период отличный от нуля называется периодической.
Основные свойства периодических функций
Если Т – период функции, то 2Т; 3Т,… и т.д. nT где n∈
 также будет периодом
также будет периодомЕсли функция f(x) имеет период Т, то функция f(ax) имеет периодом число
 ;
;
f[a(x+ )]=f(ax+Т)=f(ax).
Если f(x)ϵC[R] имеет период Т, то интеграл этой функции взятый в пределах отличающийся на Т, не зависит от выбора нижнего предела интегрирования, т.е.
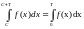 Cϵ
Cϵ
Доказательство:
y
2T
3T/2
T
T/2
0
x
S2*
S1*
S1



Сумма, разность, произведение и частное периодических функций периода Т, есть периодические функции того же периода.
§2. Ортогональные системы функций.
Вспомним
Df
скалярного произведения векторов в
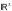 .
.

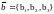
 -
это произведение можно вычислить, если
известны длины векторов и угол.
-
это произведение можно вычислить, если
известны длины векторов и угол.
Как известно в ортонормированном базисе
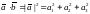
Длина вектора
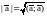
Угол

Для
того чтобы
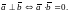

Из этого следует, что если первичным является скалярное произведение (2),
то
длину вектора и Cos
угла можно вычислить по формулам (3) и
(4). Это верно для векторов
и
для
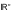 (лин.алгебра).
(лин.алгебра).
По аналогии с (2) определим скалярное произведение двух функций.
Пусть
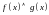 интегрируемы
в квадрате на
интегрируемы
в квадрате на
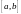 .
.
Df1.
 .
.
Замечание.
Скалярное произведение функций обладает
всеми свойствами
 .
.
Df2.
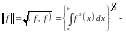 норма
(длина) функции.
норма
(длина) функции.
Функция называется нормированной, если:
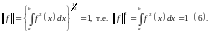
Df3. Функции называются ортогональными, если:
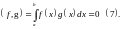
Df4.
Система
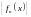 заданная
на
называется
ортогональной, если:
заданная
на
называется
ортогональной, если:
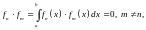 и
она называется ортонормированной, если:
и
она называется ортонормированной, если:

Замечание1.
Если система
на
ортогональна
и
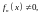 то
система
то
система
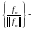 ортогональна.
ортогональна.
Доказательство.
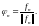
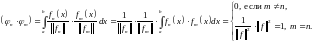
Замечание 2. В множестве функций заданных на ортонормированные системы играют роль ортонормированных базисов.
Вспомним,
что если
 о.н.б.,
то
о.н.б.,
то
 имеет разложение при этом легко видеть,
что при умножении этого разложения на
базисные вектора
имеет разложение при этом легко видеть,
что при умножении этого разложения на
базисные вектора
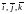 будем иметь:
будем иметь:

Если
же
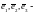 ортогональный базис и
ортогональный базис и
 то:
то:
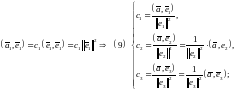

Пусть
теперь на
заданы
функция
 и
ортогональная система функций:
и
ортогональная система функций:
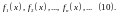
Df5. Коэффициентами Фурье функции по системе (10) называется:
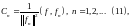 а
ряд
а
ряд
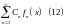 называется рядом Фурье
по системе (10).
называется рядом Фурье
по системе (10).
Замечание
1. Если
 ортонормированная
система, то
ортонормированная
система, то

Замечание 2. Коэффициенты Фурье – аналоги координат вектора в ортонормированном базисе.
Th.
(Неравенство Бесселя). Пусть
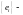 ортонормированная
система в евклидовом пространстве Е.
Тогда
ортонормированная
система в евклидовом пространстве Е.
Тогда
 имеет место неравенство Бесселя:
имеет место неравенство Бесселя:
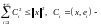 коэффициенты
Фурье элемента x
по системе
коэффициенты
Фурье элемента x
по системе
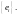
Доказательство.
Пусть
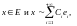 где
где
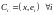 .
Рассмотрим
.
Рассмотрим
 тогда в силу ортонормированности системы
тогда в силу ортонормированности системы
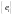 имеем
имеем
 таких, что
таких, что
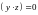 :
:
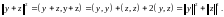
Но
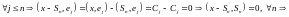
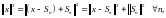 т.е.
имеет место тождество Бесселя:
т.е.
имеет место тождество Бесселя:
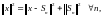 откуда
откуда
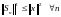 .
.
Вновь
используя ортонормированные системы
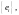 имеем
имеем
 то тогда
то тогда
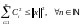 и, переходя в этом неравенстве к пределу
при
и, переходя в этом неравенстве к пределу
при
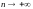 получаем неравенство Бесселя.
получаем неравенство Бесселя.
Следствие
1. (Неравенство Бесселя в
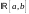 ).
).
Пусть
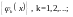 о.н.с. функций в
о.н.с. функций в
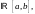
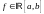 и
и
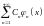 (где
(где
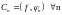 )
– ряд Фурье функции
,
тогда имеет место неравенство Бесселя:
)
– ряд Фурье функции
,
тогда имеет место неравенство Бесселя:

Следствие
2. Пусть
и
 ,
где
,
где
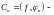 коэффициенты
Фурье для
.
коэффициенты
Фурье для
.
Тогда
из неравенства Бесселя следует сходимость
знакоположительного ряда
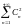 ,
а потому в силу необходимого условия
сходимости числовых рядов, имеем для
коэффициентов Фурье
,
а потому в силу необходимого условия
сходимости числовых рядов, имеем для
коэффициентов Фурье

§3. Интегралы от некоторых тригонометрических функций (вспомогательные интегралы).
I
тип.
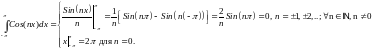
II тип.
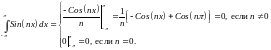
III тип.

IV тип.
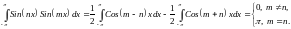
Следует иметь ввиду:
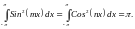
Применяют
формулы:
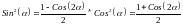 и учитывая, что
и учитывая, что
 при
при
 ,
а
,
а
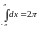 получаем
равенство IV.
получаем
равенство IV.
Если
 .
.

V.

§4. Ряд Фурье 2π-периодической функции.
Df1. Тригонометрической системой функций называется система:
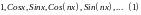 .
.
Df2. Тригонометрическим рядом называется функциональный ряд вида:
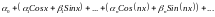 т.е.:
т.е.:
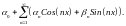
Доказательство:
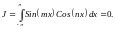
Воспользуемся
формулой
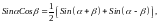 получаем:
получаем:

Если
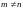 ,
то:
,
то:
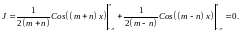
Т.к.
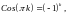 для
для
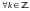
Если
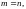 то:
то:
 для
.
для
.
Таким
образом, равенство V
справедливо для
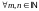 .
.
Th.
Тригонометрическая система (1) является
ортогональной на
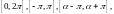 где
где
 - любое число.
- любое число.
Определим нормы системы функций (1).
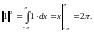

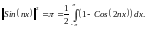
Пусть
далее функция
 периодическая,
интегрируемая функция. Её коэффициентами
Фурье являются числа.
периодическая,
интегрируемая функция. Её коэффициентами
Фурье являются числа.
(2)
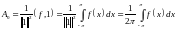
(3)
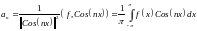
(4)
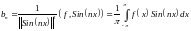 ,
,
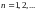
Для
удобства обозначим:
 тогда:
тогда:
(5)
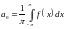
Как
видно из (5)
 получается из (3) при
получается из (3) при
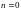 .
.
Рядом Фурье функции по системе функций (1) является ряд:
(6)
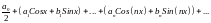 т.е.:
т.е.:
ряд
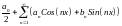 ,
где коэффициенты
,
где коэффициенты
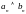 вычисляются по формулам (3) и (4).
вычисляются по формулам (3) и (4).
Замечание. Для 2π тригонометрических функций тригонометрическая система играет роль ортогонального базиса, а коэффициенты Фурье – координат.
Th. Всякий равномерно сходящийся на (-∞,+∞) тригонометрический ряд (6) является рядом Фурье для своей суммы.
