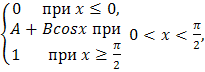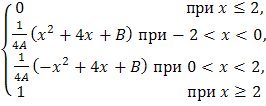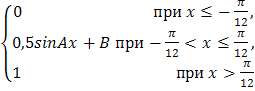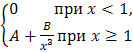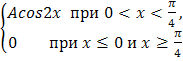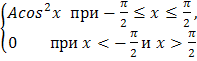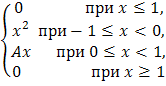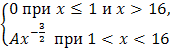Задача № 3

В вариантах 3.1 – 3.30 непрерывная СВ Х задана функцией распределения F(x).

Найти:

а) значение коэффициентов A и B,

б) плотность распределения f(x),

в) вероятность того, что СВ Х примет значение в интервале (x₁, x₂),

г) математическое ожидание и дисперсию СВ Х,

д) построить графики F(x) и f(x).

№	Функция распределения	х1	х2
3.1	F(x)=	х1=0	х2=2.5
3.2	F(x)= ,	х1=	х2=
3.3	F(x)=	х1=	х2=
3.4	F(x)=	х1=	х2=3
3.5	F(x)=	х1=	х2=1
3.6	F(x)=	х1=2	х2=4
3.7	F(x)=	х1=1,5	х2=2
3.8	F(x)=	х1=4	х2=5
3.9	F(x)=	х1=1	х2=2
3.10	F(x)=	х1= - π	х2=
3.11	F(x)=	х1=1	х2=3
3.12	F(x)=	х1=	х2=
3.13	F(x)=	х1=0	х2=T
3.14	F(x)= ,	х1= - 0,5	х2=0,5
3.15	F(x)=	х1= - 3	х2=1
3.16	F(x)=	х1=	х2=
3.17	F(x)=	х1=4	х2=9
3.18	F(x)=	х1=1,5	х2=2
3.19	F(x)=	х1= - 1	х2=2
3.20	F(x)=	х1= -1	х2=1
3.21	F(x)=	х1=	х2=
3.22	F(x)=	х1=	х2=
3.23	F(x)=	х1=0	х2=0,5
3.24	F(x)=	х1=0	х2=1
3.25	F(x)=	х1=0	х2=1
3.26	F(x)=	х1=2	х2=4
3.27	F(x)=	х1=0	х2=1
3.28	F(x)=	х1=0	х2=
3.29	F(x)=	х1= -1	х2=1
3.30	F(x)=	х1=0	х2=

Задача № 4

В вариантах 4.1 – 4.30 СВ Х задана плотностью распределения.

Найти:

а) значение коэффициента A,

б) функцию распределения F(x),

в) вероятность того, что СВ Х примет значение в интервале (x₁, x₂),

г) вероятность того, что СВ Х в n независимых испытаниях, проводимых в одинаковых условиях, ни разу не попадет в интервал (x₁, x₂),

д) математическое ожидание и среднеквадратичное отклонение СВ Х,

е) построить графики F(x) и f(x).

№	Плотность распределения	x1	x2	n
4.1	f(x)=	x1=0	x2=2	n=2
4.2	f(x)=	x1= -1	x2=1	n=2
4.3	f(x)=	x1=1	x2=3	n=4
4.4	f(x)=	x1= -1	x2=0	n=2
4.5	f(x)=Ae-λ|x| (λ>0) при -∞<x<∞	x1= -1	x2=1	n=4
4.6	f(x)=	x1= -	x2=	n=2
4.7	f(x)=	x1=0	x2=1	n=2
4.8	f(x)=	x1=0	x2=	n=2
4.9	f(x)=	x1= -1	x2=1	n=2
4.10	f(x)=	x1=0	x2=1	n=2
4.11	f(x)=	x1=2	x2=4	n=4
4.12	f(x)=	x1=0	x2=1	n=2
4.13	f(x)=	x1=0	x2=	n=2
4.14	f(x)=	x1=	x2=1	n=2
4.15	f(x)=	x1= -1	x2=1	n=2
4.16	f(x)=	x1= -	x2=	n=2
4.17	f(x)=	x1=0	x2=	n=2
4.18	f(x)=	x1=0	x2=1	n=2
4.19	f(x)=	x1=2	x2=4	n=4
4.20	f(x)=	x1= -1	x2=2	n=2
4.21	f(x)=Ae-|x-2| при -∞<x<∞	x1=1	x2=3	n=2
4.22	f(x)=	x1=	x2=	n=4
4.23	f(x)=	x1= -	x2=	n=2
4.24	f(x)=	x1=1,5	x2=2	n=2
4.25	f(x)=	x1=2	x2=3	n=2
4.26	f(x)=	x1=1	x2=2	n=2
4.27	f(x)=	x1=0,5	x2=0,5	n=2
4.28	f(x)=	x1=1	x2=4	n=4
4.29	f(x)=	x1=0,5	x2=0,5	n=3
4.30	f(x)=	x1=4	x2=9	n=4

Задача № 5.

Вариант 5.1. Задана двумерная плотность вероятности

f(x,y)=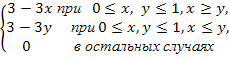

Найти f₁(x) и P(X<0,5│ y=0,75).

Вариант 5.2. Для двумерной случайной величины, равномерно распределенной на прямоугольнике [0,2]*[0,1] , найти совместную плотность распределения, вектор математических ожиданий и ковариационную матрицу.

Вариант 5.3. Двумерная случайная величина равномерно распределена внутри прямоугольника │x│ ≤2, │y│≤1. Найти ее плотность распределения, функцию распределения и вероятность попадания в круг x²+y²≤1.

Вариант 5.4. Двумерная случайная величина (X,Y) равномерно распределена внутри квадрата со стороной, равной единице, диагонали которого совпадают с осями координат.

1. Найти плотности распределения системы (X,Y) и компонент X и Y.

2. Вычислить корреляционный момент K(x,y).

3. Установить, зависимы ли X и Y.

Вариант 5.5. Двумерная случайная величина (X,Y) равномерно распределена в треугольнике, ограниченном прямыми x=0 , y=0, x+y=1.

1. Найти плотность и функцию распределения(X,Y).

2. Зависимы ли X и Y.

3. Вычислить математическое ожидание и дисперсии величин X и Y, а также корреляционный момент и коэффициент корреляции r_xy.

Вариант 5.6. Плотность распределения двумерной случайной величины (X,Y) имеет вид

f(x,y)=

1. Найти функцию распределения F(x,y).

2. Вычислить математическое ожидание MX и MY? Дисперсии DX и DY.

Вариант 5.7. Плотность распределения двумерной слцчайной величины (X,Y) имеет вид f(x,y)=

1. Найти коэффициент А.

2. Написать выражение для плотностей распределения f1(x) и f2(y)/

3. Вычислить математическое ожидание MX и MY. Средние квадратические отклонения σ_x и σ_y.

4. Установить, зависимы ли X и Y.

Вариант 5.8. Двумерная случайная величина (X,Y) равномерно распределена в треугольнике, ограниченном прямыми y=x, y=0, x=2.Найти коэффициент корреляции r_xy.

Вариант 5.9. Плотность распределения двумерной случайной величины (X,Y) имеет вид f(x,y)=A/(1+x²+y²+x²y²).

1. Найти коэффициент А.

2. Вычислить вероятность попадания случайной точки (X,Y) в прямоугольник 0≤x≤1, -1≤y≤1

3. Найти функцию распределения системы (X,Y) и компонент X и Y

4. Установить, зависимы ли X И Y.

Вариант 5.10. Двумерная случайная величина (X,Y) равномерно распределена в треугольнике, ограниченном прямыми x=0, y=0, x+y=a, где a>0.

1. Найти функцию распределения системы (X,Y) и компонент X и Y.

2. Найти условную плотность распределения f(y/x).

Вариант 5.11. Плотность распределения двумерной случайной величины (X,Y) имеет вид

f(x,y)=

Найти функцию распределения системы (X,Y) и коэффициент корреляции r_xy.

Вариант 5.12. Независимые случайные величины (X,Y) имеют равномерные распределения соответственно в интервалах (-1,1) и (0,2).

1. Найти плотность и функцию распределения системы (X,Y) .

2. Вычислить математическое ожидание MX и MY и дисперсию DX и DY.

Вариант 5.13.Двумерная случайная величина (X,Y) равномерно распределена в прямоугольнике, ограниченном прямыми x=0, x=a, y=0,y=b.

1. Найти плотность и функцию распределения системы (X,Y)

2. Вычислить математическое ожидание MX и MY и дисперсию DX и DY.

Вариант 5.14. Двумерная случайная величина (X,Y) равномерно распределена в треугольнике, ограниченном прямыми x=a, y=a,x+y=a ,где a>0.Найти плотности и функции распределения системы (X,Y) и компонент X и Y, а также условные плотности распределения f(y/x), f(x/y).

Вариант 5.15. Двумерная случайная величина (X,Y) равномерно распределена внутри квадрата, диагонали которого совпадают с осями координат, а сторона равна a.

1. Найти плотности распределения системы (X,Y) и компонент X и Y.

2. Вычислить корреляционный момент K(x,y)

3. Установить, зависимы ли X и Y.

Вариант 5.16. Плотность распределения двумерной случайной величины (X,Y) имеют вид

f(x,y)=

Найти функцию распределения системы (X,Y) и коэффициент корреляции r_xy.

Вариант 5.17. Двумерная случайная величина (X,Y) равномерно распределена в треугольнике, ограниченном прямыми y=-b/a, y=0, x=a ,где а>0 и b>0.

Вычислить Математические ожидание и дисперсии и коэффициент корреляции.

Вариант 5.18. Плотность распределения двумерной случайной величины (X,Y) имеет вид

f(x,y)=

1) Найти коэффициент А.

2) Вычислить математические ожидания MX и MY и дисперсии DX и DY и вероятность попадания случайной точки (X,Y) в квадрат, вписанный в окружность =1.

Вариант 5.19. Двумерная случайная величина (X,Y) равномерно распределена в треугольнике, ограниченном прямыми x=0, y=0, x/a+y/a=1, где a>0, b>0.

Вычислить математические ожидания MX, MY дисперсии DX и DY, и коэффициент корреляции.

Вариант 5.20. Плотность распределения двумерной случайной величины (X,Y) имеет вид

f(x,y)=

Найти значение коэффициента А и плотностей распределения f1(x) и f(x/y).

Вариант 5.21. Вследствие случайных погрешностей измерения сторон прямоугольника, X и Y образуют двумерную случайную величину с плотностью распределения

f(x,y)= A/π²(x²+16)(y²+25)

Найти коэффициент А и плотности распределения системы (X,Y) и компонент X и Y .Доказать, что X и Y независимы.

Вариант 5.22. Двумерная случайная величина (X,Y) равномерно распределена в треугольнике, ограниченном прямыми y=x, x=0, y=2.Найт коэффициент корреляции.

Вариант 5.23. Плотность распределения двумерной СВ (X,Y) имеет вид

F(x,y)=A/1+(x²+y²)²

Найти коэффициент А и вероятность попадания случайной точки (X,Y) в круг с центром в начале координат и радиусом, равным единице.

Вариант 5.24. Показать,что случайные величины X и Y с двумерной плотностью распределения независимы.

f(x,y)=

Найти математическое ожидание и дисперсию составляющей X.

Вариант 5.25. Двумерная СВ (X,Y) равномерно распределена внутри круга

x² +y²≤R². Найти плотности распределения f(x,y) f1(x), f2(y), f(x/y) и корреляционный момент.

Вариант 5.26. Плотность совместного распределения случайных величин X и Y:

f(x,y)=

1. Найти постоянную c. 2) Вычислить корреляционный момент K_xy . 3) Установить, зависимы ли X и Y.

Вариант 5.27. Плотность совместного распределения СВ X и Y задана формулой:

f(x,y)=

1. Найти постоянную c 2) Записать функцию распределения F(x,y) 3)Вычислить коэффициент корреляции r_xy.

Вариант 5.28. Плотность распределения двумерной величины (X,Y) равна

f(x,y)=

1. Определить значение А.

2) Установить, зависимы ли X и Y

3) Найти К_xy , если X и Y зависимы.

Вариант 5.29. Плотность распределения двумерной СВ (X,Y) имеет вид

f(x,y)=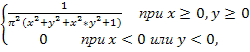

1. Найти функцию распределения F(x,y). 2) Установить, зависимы ли X,Y.

Вариант 5.30. Двумерная СВ (X,Y) равномерно распределена внутри квадрата

0≤x≤4, 0≤y≤4. Найти функцию распределения и плотность распределения, а также вероятность попадания случайной точки (X,Y) внутрь круга x²+y²<2.
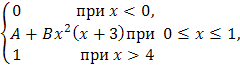
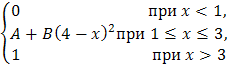