2.4 Рекуррентные соотношения

Вычисление по формулам (4) и (5)

(4)

(5)

коэффициентов 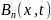и 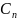практически возможно лишь в очень редких случаях, но из этих формул получаются следующие рекуррентные соотношения:

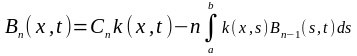(6)

(7)

Зная, что коэффициент 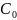=1 и по формулам (6) и (7) найдем последовательно 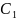, 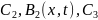и т.д.

Пример 2. Нахождения резольвенты ядра с помощью рекуррентных соотношений:

Пользуясь формулами (6) и (7) найти резольвенту ядра 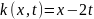, где

Решение. Имеем =1, 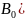) = . Пользуясь формулой (7) найдем:

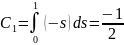
По формуле (6) получим:

Далее будем иметь:

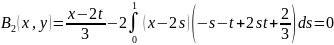
Следовательно,

Резольвента данного ядра будет:

2.5 Метод последовательных приближений

Мы докажем существование уравнения

(11)

(при достаточно малых ) методом последовательных приближений.

Для простоты выкладок будем предполагать, что:

1. ядро непрерывно в квадрате ; тогда оно ограничено некоторой константой

2. функция f(x) непрерывна на отрезке , следовательно, она ограничена на этом отрезке некоторой константой

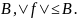
Построим последовательность функций

φ ₁(x),φ₂(x),…,φ_n(x)

по следующему правилу:

где φ ₀(s) – произвольная фиксированная непрерывная функция.

Теорема. Последовательность (12) – (14) функций φ_n(x) равномерно сходится на отрезке [a, b], к функции φ(x), являющейся решением уравнения (11) при .

Доказательство:

Преобразуем формулы для получения φ_n(x). Подставляя функцию φ₁(x) в φ₂(x), получим:

Меняя в последнем интеграле порядок интегрирования, получим:

K₁(x, s)=k(x, s),

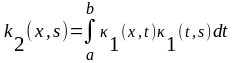
Аналогично находим:

,

где . Предел функции φ_n(x), если он существует, равен сумме ряда:

(15)

Докажем равномерную сходимость ряда. Для этого оценим интегралы:

Имеем

Поэтому

Следовательно, числовой ряд

(16)

является мажорантным для ряда (15). Если , то ряд (16) сходится. Следовательно, при таких λ ряд (16) сходится, а вместе с ним и последовательность функций φ_n(x) равномерно сходится к функции . Эта функция является решением уравнения (11). В самом деле, переходя в формуле (14) к пределу при n→ ∞, получим

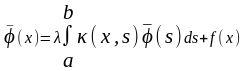
Переход к пределу под знаком интеграла здесь закончен, так как последовательность сходится равномерно.

Заметим, что предел не зависит от выбора функции φ₀(x)(нулевого приближения). В самом деле, если существует еще одно решение ψ(x) уравнения (11), то, полагая в процедуре построения функций (12) – (14) φ₀(x)= ψ(x), получим

φ₁(x)= ψ(x), φ₂(x)= ψ(x),…, φ_n(x)= ψ(x)…

Эта последовательность имеет пределом функцию . Но вместе с тем очевидно:

Таким образом, =ψ(x). Теорема доказана.

Поскольку ряд (16) сходится при , то при таких же λ сходится и ряд:

Но этот ряд является мажорантным для ряда:

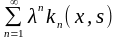(17)

Следовательно, ряд (17) сходится равномерно. Поэтому ряд (15) можно записать в виде:

или

(18)

где функция

называется резольвентой уравнения (11).

Пример 3. Решить интегральное уравнение , 0≤x≤1 методом последовательных приближений. Здесь k(x, t)=xt, a=0, b=1.

Решение. Последовательно найдем

K₁(x, t)=xt,

Согласно формуле

Получим

,

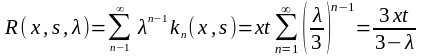причем |λ|<3 и в силу формулы:

решение данного интегрального уравнения запишется в форме:

, 0≤x≤1, λ≠3

В частности, при f(x)=x получим

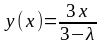, 0≤x≤1, λ≠3