Учреждение образования

«Белорусский государственный педагогический университет

имени Максима Танка»

Физико-математический факультет

Кафедра математического анализа

Интегральные уравнения

Курсовая работа

студентки 403группы

4 курса специальности

«Математика. Информатика»

Допущена к защите дневной формы

получения образования

___________ Торчило

Заведующий кафедрой _____ __________ Натальи Михайловны

(подпись) (фамилия, инициалы)

Протокол № ___ от __________2015 г.

Научный руководитель -

Защищена__________2015 г. Старший преподаватель

с отметкой «_____________» _________ О.Г.Медведева

Минск, 2015

Оглавление

Введение…………………………………………………………….…………3

1. Физические задачи, приводящие к понятию интегрального уравнения 5

2. Классификация и некоторые методы решения интегральных уравнений 12

2.1 Уравнения Фредгольма первого и второго рода…...……..………..12

2.2 Метод определителей Фредгольма………………………….………14

2.3 Пример нахождения резольвенты ядра…………………….……….16

2.4 Рекуррентные соотношения………………………………….……...17

2.5 Метод последовательных приближений………………….………...18

2.6 Уравнения Вольтерра……………………………………………..….23

2.7 Метод сведения к алгебраическому уравнению………………..…..23

2.8 Нелинейный уравнения…………………………………………..…..26

Заключение 28

Список литературы 29

Введение

Курсовая работа посвящена теме интегральные уравнения.

Целью моей работы является рассмотрение особенностей интегральных уравнений и изучение методов их решения.

Для достижения цели были определены следующие задачи:

1. Рассмотрение физических задач, приводящих к понятию интегрального уравнения

2. Изучение классификации и некоторых методов решения интегральных уравнений.

Едва ли не первой задачей, которую можно связать с интегральными уравнениями, была задача обращения интеграла

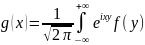dy , (I)

то есть нахождения функции по данной функции . Решение ее получил Фурье в 1811 году в виде

dx. (II)

Можно считать, что формула (II) дает решение интегрального уравнения (I), в котором - искомая, а - данная функция, и наоборот.

Формулы (I) и (II), как известно, называются формулами обращения Фурье.

К интегральным уравнениям приводит задача Коши для обыкновенных дифференциальных уравнений

,

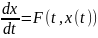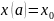
Таким образом, решение интегрального уравнения эквивалентно решению задачи Коши.

Прежде, чем рассмотреть некоторые методы решения интегральных уравнений, следует заметить, что для них, как и для дифференциальных уравнений не всегда удается получить точное аналитическое решение. Выбор метода решения зависит от вида уравнения. В данной курсовой работе будут рассмотрены несколько методов для решения линейных и нелинейных интегральных уравнений.

Курсовая работа состоит из введения, основной части, заключения, списка используемой литературы. Во введении определены цель и сформулированы задачи.

В заключении подведены общие итоги курсовой работы, изложены основные выводы по данной работе.

1.Физические задачи, приводящие к понятию интегрального уравнения

Задача Абеля. В 1823 г. Абель, занимаясь обобщением задачи о таутохроне, пришел к уравнению

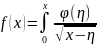
где 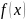— заданная функция, а — искомая функция. Это уравнение есть частный случай линейного интегрального уравнения Вольтерра 1-го рода

Уравнение Абеля интересно в том отношении, что оно является одним из интегральных уравнений, к которым непосредственно приводит постановка той или иной конкретной задачи механики или физики.

Исторически задача Абеля представляет первую задачу, которая привела к необходимости рассмотрения интегральных уравнений.

Задача Абеля состоит в следующем. «Материальная точка под действием силы тяжести движется в вертикальной плоскости (ξ, ) по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x, достигла оси Оξ за время t=f₁(x), где f₁(x) - заданная функция». (Рисунок-1).

Абсолютная величина скорости движущейся точки

Обозначим через ß= ß( )- угол наклона касательной к оси Оξ. Тогда будем иметь

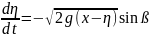
(составляющая скорости по оси О ).

Отсюда

Интегрируя по в пределах от 0 до х и пологая , получим уравнение Абеля

Обозначая через 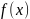, окончательно будем иметь

Здесь - искомая функция, - заданная функция.

Рисунок-1

Найдя , мы можем составить уравнение искомой кривой. В самом деле, =1/sinß, откуда =Ф(ß).

Далее,

так что

Таким образом, искомая кривая определяется параметрическими уравнениями

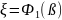, =Ф(ß).

В частности, при f(x)=C=const такой кривой является циклоида.

Рассмотрим ещё задачу, приводящую к интегральным уравнениям.

Пусть имеем упругую нить длины l, которая легко, без сопротивления, изменяет свою форму, но для увеличения длины которой на ∆l нужна сила ɤ∆l, где ɤ- некоторая постоянная (закон Гука).

Пусть концы нити закреплены в точках A и B. Когда нить находится в покое под действием только

горизонтальной растягивающей силы T₀, очень большой по сравнению с другими рассматриваемыми силами, положение нити будет совпадать с отрезком AB оси Ox.

Допустим, что в точке C₀, для которой x=ξ, приложена к нити вертикальная сила P. Под ее влиянием нить примет форму ломаной АСВ. Будем считать С C₀ очень малым по сравнению с АC₀ и C₀В (результат малости Р по сравнению с T₀). Будем также считать, что натяжение нити осталось равным T₀ и под действием силы Р. Проектируя на вертикаль силы натяжения нити в точке С и силу Р, из условия равновесия получим

T₀sinα + T₀ sinβ = P.

Вследствие малости величины δ имеем

sinα≈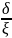 , sinβ≈ ,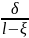

так что условие можно записать в виде

T₀ + T₀ = P.

Откуда

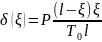
Обозначая через 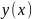прогиб нити в точке с абсциссой х. получим

где

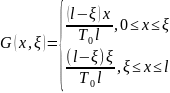
Действительно, пусть x < ξ. Из подобных треугольников AC₀C и AA₁С₁ находим

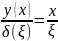
Или

Следовательно,

Нетрудно видеть, что .

Если на нить действует непрерывно распределенная сила с линейной плотностью p(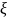 ), то на участок нити между точками и действует сила, приблизительно равная p( ) , которая вызывает смещение . Так как смещение, обусловленные элементарными силами p( ) , суммируются(принцип суперпозиции), то под действием всех нагрузок, отклонение будет приближенно равно

,

что при →0 дает . Функция носит название функции влияния.

Рассмотрим следующие задачи.

Будем искать плотность распределения силы , под влиянием которой нить примет заданную форму . Тогда мы придем к интегральному уравнению Фредгольма 1-го рода

относительно искомой функции .

Допустим, что на нить действует меняющаяся со временем t сила с плотностью в точке :

( )

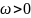Под ее влиянием нить придет в движение. Будем предполагать, что при движении нити абсцисса каждой ее точки не меняется и то нить совершает периодические колебания, описываемые уравнением

Пусть ρ(ξ)- линейная плотность массы нити в точке ξ. Тогда в момент t на участок нити между точками и , кроме силы , действует ещё сила инерции

- ρ(ξ) .

Поэтому равенство примет следующий вид:

Сокращаем на 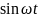и полагая

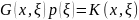
получим

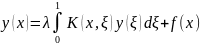
Считая функцию р ( ), а следовательно и , заданной, приходим к интегральному уравнению Фредгольма 2-го рода для определения функции .

В заключение приведем так называемое уравнение переноса, играющее большую роль в современной физике (например, в процессах замедления нейтронов) и представляющее собой пример интегро-дифференциального уравнения.

Будем предполагать, что нейтроны не испытывают неупругих столкновений и что энергия нейтрона достаточно мала. Пусть Ω будет единичным вектором, определяющим направление потока нейтронов с энергией Е.

Введем безразмерную величину u, определяемую соотношением

где 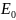— начальная энергия. Обозначим через N (г, Ω, , t)drdΩdu число нейтронов, координаты которых лежат между г а г + dr, направления скоростей — между Ω и Ω+ dΩ, а величина энергии заключена в пределах, соответствующих значениям параметра от до + du. Все эти данные относятся к моменту времени t. Можно показать, что изменение со временем функции распределения нейтронов при движении потока нейтронов в направлении Ω равно

(v — скорость потока).

Обозначим через l_s( ) среднюю длину свободного пробега нейтрона при рассеянии, а через l( ) — полную среднюю длину свободного пробега.

Число нейтронов, удаленных из потока благодаря процессам рассеяния и захвата, равно

Отнесенное к единице времени число столкновений, которые испытывают нейтроны со скоростями, определяемыми параметрами Ω^’, u^' в момент времени t в точке r, равно

Обозначим через f (μ₀, u-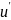 ) вероятность того, что нейтрон, имевший до столкновения скорость, характеризуемую значениями параметров { Ω^’ , u^' }, после столкновения будет иметь скорость, характеризуемую, значениями пара- параметров {Ω,u}. Здесь μ₀=(Ω, Ω^’ ) — косинус угла рассеяния нейтрона. Будем считать, что функция f (μ₀, u- ) нормирована к единице, т. е. что

точнее,

( ).

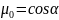Число нейтронов, которые присоединяются к рассматриваемому потоку нейтронов в результате рассеяния, определяется выражением

,

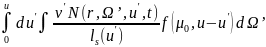где во внутреннем интеграле интегрирование ведется по всевозможным направлениям Ω^’ .

Наконец, обозначим через

отнесенное к единице времени и единице объема число нейтронов, порожденных в точке г в момент времени t.

Принимая во внимание уравнение непрерывности и используя выражения, заключаем, что функция удовлетворяет следующему уравнению переноса:

Вводя вместо функции N функцию

и учитывая, что , можно записать уравнение в эквивалентной форме:

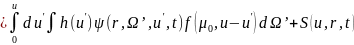
где

Функция входит в уравнение как под знаком производной, так и под знаком интеграла; уравнения такого вида называются интегро-дифференциальными.

Основная задача теории переноса заключается в решении интегро-дифференциального уравнения, что в общем случае сопряжено с огромными трудностями.