3.5.3. Расчет регулятора

Для выполнения расчета логарифмических частотных характеристик необходимо нажать кнопку Linearize Model в правом поле окна Control and Estimation Tools Manager .

После окончания расчета в появившемся окне LTI Viewer: Linearization Quick Plot выводится график переходного процесса системы при единичном ступенчатом воздействии в точке входа.

Для получения логарифмической амплитудной характеристики (ЛАХ) и логарифмической фазовой характеристики (ЛФХ) выбираем тип графика Bode, нажав правую кнопку мыши в поле графика и выбрав в открывшемся меню пункт Plot Type/Bode. В этом же меню устанавливаем сетку Grid.

На рисунке 6 показана логарифмическая частотная характеристика системы с разомкнутой обратной связью. При помощи указателя мыши можно выделить любую точку на графиках и узнать её координаты. Вызвав правой кнопкой контекстное меню Characteristics, можем автоматически поместить характерные точки (частота среза и др.). По виду логарифмических характеристик разомкнутой системы видно, что ЛАХ пересекает ось абсцисс с наклоном в -40 дб/дек, что свидетельствует о неустойчивом процессе в системе. Запас устойчивости по фазе φ_з=11.3⁰, частота среза ω_c=-26,6 рад/с

Рис. 6. Частотные характеристики ненастроенной системы

Для того чтобы система была устойчивой необходимо уменьшить частоту среза, при этом необходимо обеспечить запас по фазе 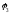≥20⁰, желательно так же избежать перерегулирования.

Для того чтобы в системе не было перерегулирования ЛАХ должна пересекать нулевую ось но участке – 20Дб/дек. При этом данный участок должен сохраняться в районе 0,8 декады от точки пересечения.

По виду желаемых частотных характеристик можем определить, что для соблюдения вышеперечисленных условий необходимо опустить ЛАХ на 70 дБ, что соответствует уменьшению коэффициента усиления системы в 3030раз: 3030

Для этого уменьшим коэффициент усиления интегрального канала ПИД-регулятора в 3030раз, в результате чего он составит k_и = 0,00033.

k_и = 0,00033

Структурному блоку ПИД-регулятора зададим новые параметры регулятора.

Заново произведем расчет модели и получим новые логарифмические частотные характеристики исследуемой системы (рисунок 7).

Рис. 7. Частотные характеристики настроенной системы

После этого вновь замыкаем систему и анализируем график переходного процесса (рисунок 8), по графику видно, что процесс в системе апериодический, перерегулирование δ = 0%, статическая ошибка X_СТ = 0, время переходного процесса t_пп= 21,3 с.

Рис. 8. Переходный процесс в системе

Заключение

В работе производился выбор регулятора в системе регулирования расхода и определение его настроек, оценка качества полученной в результате настройки системы. На основе анализа математической модели системы, ее частотных характеристик был выбран ПИД-регулятор со следующими параметрами:

- коэффициент усиления пропорционального канала регулятора

K_п = 0,0000145

- коэффициент усиления интегрального канала регулятора

K_и = 0,00033

- коэффициент усиления дифференциального канала регулятора

K_д = 0,000000223

Вышеуказанные настройки обеспечивают плавный сходящийся апериодический переходный процесс в системе с отсутствием перерегулирования и статической ошибки. Время переходного процесса в системе составляет t_пп=21,3 с.

На основании изложенного принимаем выбранный тип регулятора и указанные настройки как рекомендуемые для использования.