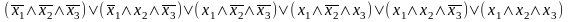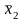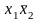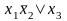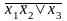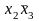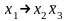- •Изложить теоретический вопрос
- •Решить задачи на темы: “Подсчет количества информации”и «Арифметические основы эвм»
- •Измерьте объем следующего информационного сообщения в битах, байтах, килобайтах и мегабайтах: "Ах, не глухих теплиц цветы благоуханны и красивы…"
- •Записать сообщение из фамилии, имени, отчества и вычислить по формуле Шеннона среднюю информационную емкость символа сообщения. Оценить информационную емкость всего сообщения.
- •Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке находится 50 белых, 25красных, 25 синих шариков.
- •Перевести в десятичную систему счисления следующее двоичное число 1010101010
- •Перевести десятичное число a в g-е системы счисления
- •Перевести десятичные числа в двоичные с точностью до 2–8. Для полученных двоичных чисел записать прямой, обратный и дополнительный коды (0,2778; –0,7705)
- •Каждое число из задания 8 умножьте на 100, переведите в двоичный код (точность – 6 разрядов) и выполните сложение и вычитание полученных чисел
- •Решить задачи на тему «Логические основы эвм»
- •Запишите символически следующие сложные предложения, употребляя буквы для обозначения простых компонентов предложения "Если Вася умеет писать или читать, то он грамотный человек".
- •Составить таблицу истинности для логического выражения f:
- •По таблице истинности из задания 2 построить сднф и скнф функции f.
- •Упростить формулу из задания № 3.2
- •По полученной упрощенной формуле составить функциональную и контактную схемы
- •Интерполировать табличные данные с помощью полинома Лагранжа.
- •Список литературы
Решить задачи на тему «Логические основы эвм»
Запишите символически следующие сложные предложения, употребляя буквы для обозначения простых компонентов предложения "Если Вася умеет писать или читать, то он грамотный человек".
А = "Вася умеет писать",
B = "Вася умеет читать",
C = "Вася - грамотный человек"
Ответ: (A ˅ B) C
Составить таблицу истинности для логического выражения f:
x1 |
x2 |
x3 |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
По таблице истинности из задания 2 построить сднф и скнф функции f.
Для нахождения СКНФ нужно из таблицы истинности выделить лишь те строки, результат которых равен 0. Для данной функции набор строк будет следующим:
x1 |
x2 |
x3 |
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
Далее, для каждой строки выписываем дизъюнкцию всех переменных по следующему алгоритму: если значение переменной в данной строке равно 0, то в дизъюнкцию записываем саму переменную, а если равно 1, то - отрицание этой переменной. После этого все дизъюнкции связываем в конъюнкцию.
СКНФ:

Для нахождения СДНФ нужно из таблицы истинности выделить лишь те строки, результат которых равен 1. Для данной функции набор строк будет следующим:
x1 |
x2 |
x3 |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
Далее, для каждой строки выписываем конъюнкцию всех переменных по следующему алгоритму: если значение переменной в данной строке равно 1, то в конъюнкцию записываем саму переменную, а если равно 0, то - отрицание этой переменной. После этого все конъюнкции связываем в дизъюнкцию.
СДНФ: