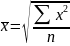Решение типовых задач

Средняя величина является обобщающей характеристикой совокупности. Она обобщает многие индивидуальные величины и нужна для измерения уровня признака совокупности в данных конкретных условиях места и времени и для сравнения уровней признака в разных совокупностях. Эти качества средней имеют исключительно важное значение для анализа, особенно для выявления и изучения закономерностей жизни общества.

Средние величины статистика применяет как для целостной характеристики системы, совокупности, так и для характеристики отдельных подсистем, отдельных типических групп, составляющих систему, совокупность. Средние, характеризующие систему, совокупность в целом, называются системными или общими средними, а средние, характеризующие подсистемы, типические группы и подгруппы, называются групповыми или подсистемными.

Системные (общие) и групповые (подсистемные) средние являются реальными средними, так как они характеризуют реальные системы, подсистемы и группы единиц совокупности, но они отличаются друг от друга по существу. Групповая (подсистемная) средняя, поскольку она относится к однородной совокупности, количественно выражает то или иное свойство ее и в то же время типична для каждой единицы этой совокупности как ее часть. Системная же средняя как средняя, относящаяся к совокупности разнородных частей, групп и единиц, но органически связанных между собой в систему, количественно выражает то или иное свойство системы, но не типична для отдельных частей, групп и единиц, составляющих систему.

Все средние величины делятся на: степенные средние и структурные средние. Среди степенных средних выделяются: средняя арифметическая, средняя гармоническая, средняя геометрическая. Каждый вид средней имеет свои особые свойства, которые наиболее полно соответствуют решению определенной задачи. Поэтому одним из основных вопросов, который возникает при использовании средних, является выбор способа расчета, т.е. формы средней. Форму средней выбирают исходя из экономической сущности осредняемого признака. Средние вычисляются в форме простых и взвешенных средних. Простой средней пользуются только в тех случаях, когда у каждого варианта частота равна единице, либо когда все частоты равны между собой.

Формулы различных степенных средних величин

Наименование средней	Формула средней
	простая	взвешенная
Арифметическая
Гармоническая
Геометрическая	;
Квадратическая

Средняя арифметическая и средняя гармоническая наиболее распространенные виды средней, получившие широкое применения в плановых расчетах, при расчете общей средней из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Выбор средней арифметической и средней гармонической определяется характером имеющейся в распоряжении исследователя информации.

Средняя квадратическая применяется для расчета среднего квадратического отклонения (σ), являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов).

Средняя геометрическая (простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики, если промежутки времени, к которым относятся коэффициенты роста, одинаковы. Если средние коэффициенты роста относятся к периодам различной продолжительности, то общий средний коэффициент роста за весь период определяется по формуле средней геометрической взвешенной.

Среди структурных средних, характеризующих структуру совокупности, наиболее известны мода и медиана.

Мода и медиана в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач.

Медиана (Ме) – значение изучаемого признака, которое по своей величине занимает серединное место в ряду вариантов, расположенных в порядке их возрастания или убывания. Такой ряд называется ранжированным. Примером такого ряда может служить месячная заработная плата рабочих цеха.

Порядковый номер рабочего	1	2	3	4	5	6	7	Итого
Месячная заработная плата, руб	90	105	148	160	175	220	250	1148

В этом ряду среднее место по размеру заработной платы занимает рабочий с номером 4, получивший 160 руб. эта величина и есть медиана. Меньше и больше медианы одинаковое число вариантов. Порядковый номер, которому соответствует медиана, определяется по формуле:

Если количество вариантов в ряду четное число, т.е., если бы в цехе был еще и восьмой рабочий с заработной платой 276 руб., то медиана находилась бы посередине между четвертым и пятым порядковыми номерами.

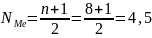В таких случаях принято считать, что в промежутке между номерами идет равномерное нарастание или убывание вариантов. Поэтому за медиану принимают среднюю арифметическую из вариантов с номерами четыре и пять. В данном примере Ме = (х₄ +х₅) / 2 = (160+175) / 2 = 167,5 руб.

Смысл полученного результата такой: одна половина рабочих получила за месяц меньше, а другая – больше 167,5 руб. Медиана, следовательно, обобщающий показатель распределения совокупности, уровень признака, который делит совокупность на две равные части.

Приведенный пример вычисления медианы относится к случаю, когда расчет производится на основе индивидуальных значений признака. Обычно же в статистике приходится иметь дело со сгруппированными данными в форме дискретных и интервальных рядов. В таком случае медиана вычисляется по следующей формуле:

где х_е – нижняя граница медианного интервала; h – величина медианного интервала; ∑f –сумма частот или частостей ряда; S _{mе – 1} - сумма накопленных частот в интервалах, предшествующих медианному; f_mе – частота медианного интервала.

Мода (Мо) – это вариант признака, который при данном сочетании причин разного порядка чаще всего встречается в вариационном ряду. Например, цена, по которой чаще всего реализуется данный товар на рынке, является модой или модальной ценой. Месячная заработная плата, которая чаще встречается в данном коллективе, является для него модальной заработной платой. Мода отвечает на вопрос о том, какое значение изучаемой переменной величины наиболее вероятно. То, что в статистике принято называть модой, считается в обычной жизни массовым, типичным, типическим.

В дискретных рядах мода легко определяется как вариант, которому соответствует максимальная частота. Определение моды в интервальных рядах требует расче­та по формуле:

f_mo – f_mo-1

Mo = x_mo + h ----------------------------------,

(f_mo – f_mo-1) + (f_mo – f_mo+1)

где х_mo — нижняя граница модального интервала; h — величина мо­дального интервала; f_mo — частота модального интервала; f_mo+1 — частота интервала, следующего за модальным; f_mo-1 — частота ин­тервала, предшествующего модальному.

В средней находит отражение то общее, что свойственно всем единицам со­вокупности. Но каждой единице свойственны и индивидуальные особенности, которые ведут к отклонениям от среднего уровня. Таковы, например, отклонения выработки отдельных рабочих от средней выработки по цеху, которые имеют место даже, если все рабочие производят одни и те же изделия из одного и того же сырья и на одних и тех же станках. Эти отклонения вызваны индивидуальными особенностями рабочих - опытом и знанием дела, состоянием здоровья и самочувствием, сообразительностью и ини­циативностью и т. п. Поэтому изучение отклонений от средней, их причины, масштабы, а также закономерности их распределения представляет большой практический и теоретический интерес. Эти задачи решаются в определенной мере при помощи показателей вариации.

К абсолютным показателям вариации относятся:

• размах вариации (колебаний);

• среднее линейное отклонение;

• среднее квадратическое отклонения;

• дисперсия.

Размахом вариации называют амплитуду колебаний, опре­деляемую как разность между максимальным и минимальным зна­чениями признака, положенного в основу ряда распределения. Ес­ли обозначить максимальное значение х_max, а минимальное — х_min, то размах вариации R равен:

R = x_max — x_min, где х — вариант при­знака. Этот показатель представляет интерес в тех случаях, когда важно знать, какова амплитуда колебания признака и в каких пределах он колеблется.

Среднее линейное отклонение ( ) и среднее квадратическое отклонение (σ) показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.

Среднее линейное отклонение определяется по формулам:

а) для несгруппированных данных

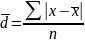
б) для вариационного ряда

Среднее квадратическое отклонение (σ) и дисперсия (σ²) определяются так:

а) для несгруппированных данных

б) для вариационного ряда

Формула для расчета дисперсии может быть преобразована:

т.е. дисперсия равна средней из квадратов индивидуальных значений признака минус квадрат средней величины.

При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической используются относительные показатели вариации.

Наиболее часто применяется коэффициент вариации. Его применяют не только для сравнительной оценки вариации, но и для характеристики однородной совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному):

Кроме общей средней для всей совокупности исчисляются средние по отдельным группам (групповые или частные средние) и три показателя дисперсии:

• общая дисперсия;

• межгрупповая дисперсия;

• средняя внутригрупповая дисперсия.

Величина общей дисперсии (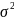 ) характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности, и определяется по формуле:

где - общая средняя арифметическая для всей изучаемой совокупности.

Межгрупповая дисперсия (дисперсия групповых средних ) отражает систематическую вариацию, т.е. те различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки. Межгрупповая дисперсия определяется по формуле:

где -средняя по отдельной группе;

- число единиц в определенной группе.

Средняя внутригрупповая дисперсия ( ) характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.

Средняя внутригрупповая дисперсия определяется по формуле:

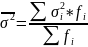
где - дисперсия по отдельной группе:

Указанные дисперсии взаимосвязаны между собой следующим равенством: величина общей дисперсии равна сумме межгрупповой дисперсии и средней внутригрупповой дисперсии:

Это тождество отражает закон (правило) сложения дисперсий. Опираясь на это правило, можно определить, какая часть (доля) общей дисперсии складывается под влиянием признака-фактора, положенного в основу группировки.

Существует также вариация альтернативного признака. Альтернативный признак – качественный признак, имеющий две взаимоисключающие разновидности (например, работники предприятия подразделяются на мужчин и женщин; продукция-на годную и бракованную и т.д.).

Альтернативный признак принимает всего два значения:

1-наличие признака;

0-отсутствие признака.

p+q=1,

где р – доли единиц, обладающих признаком;

q –доли единиц, не обладающих признаком.

Среднее значение альтернативного признака

Дисперсия альтернативного признака

Предельное значение вариации альтернативного признака равно 0,25; оно получается при p=q=0,5.