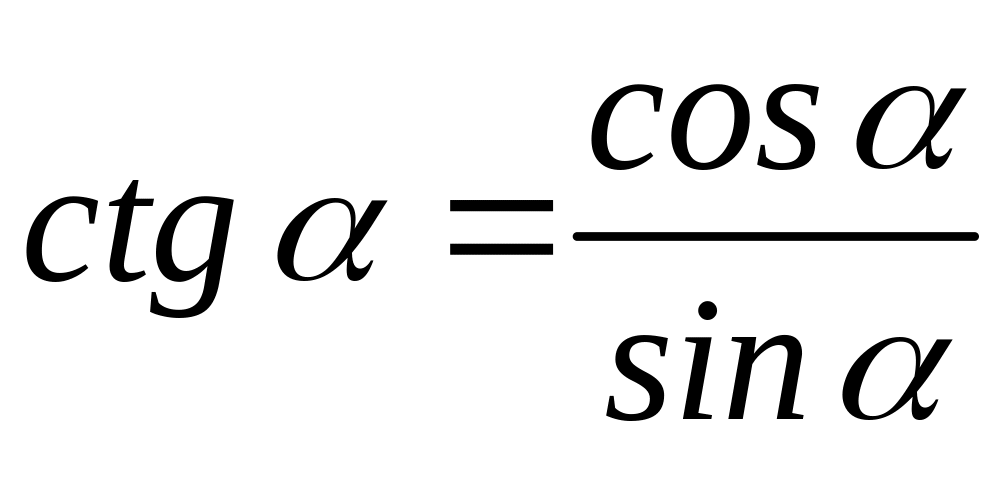2.3. Формулы приведения
Теорема сложения для синуса. При произвольных значениях и имеют место теоремы сложения:
.
Доказательство.
Синус угла
равен косинусу аргумента
,
т.е.
,
рис. 2.7. Этот аргумент можно представить
следующим образом
Т
Рис. 2.7
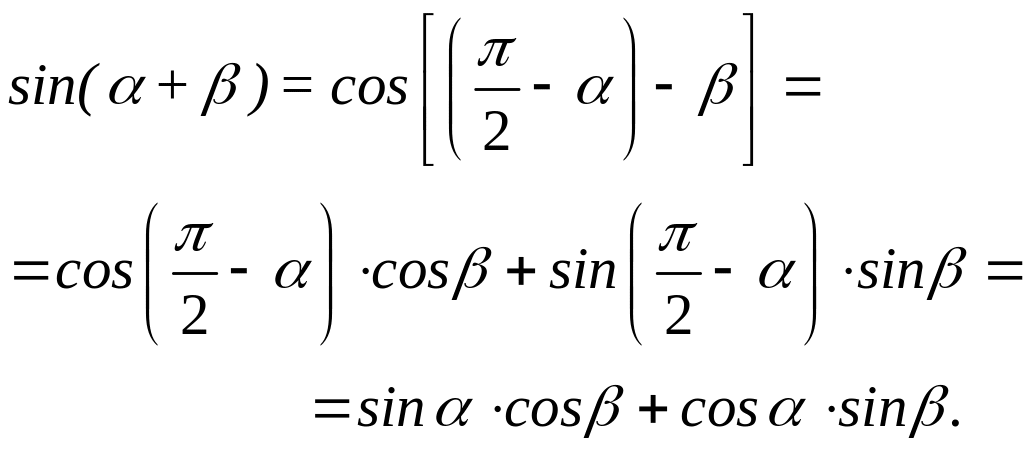(5)
Заменив на в формуле (5), получим
Следствие. Если углы , получим из (5)
.
Пример
2.5.
Вычислить
,
,
,
.
Решение.
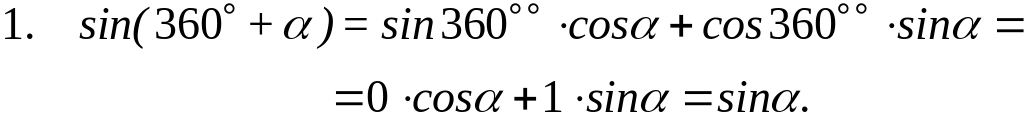
Пример
2.6.
Вычислить
Решение. Имеем:
Получили,
что
Пример
2.7.
Вычислить
Решение. Имеем:
Получили,
что
Функции суммы и разности углов сведем в одну таблицу 2.1
Таблица 2.1
|
Рассмотрим формулы:
;
1.
При
.
Тогда:
;
.
2.
При
.
Тогда:
;
.
3. При
.
Тогда:
4.
При
.
Тогда:
;
.
Значимые формулы приведения можно свести в одну таблицу 2.2.
Таблица 2.2
|
;
;
.
Рассмотрим формулы:
;
1. При . Тогда:
;
.
2. При . Тогда:
;
.
3. При . Тогда:
;
.
4. При . Тогда:
.
Значимые формулы приведения можно свести в одну таблицу 2.3.
Таблица 2.3
|
;
;
.
Эмпирические
правила.
Формул приведения много. Любую формулу
приведения можно получить, зная значения
тригонометрических функций в первой
четверти, т. е. для углов
(значения тригонометрических функций
в смысле главного значения) и зная знак
тригонометрической функции в различных
четвертях (квадрантах), рис. 2.8. Анализируя
вывод формул приведения, приведенных
в таблицах 2.1–2.2, можно сформулировать
общие два эмпирических правила, которыми
следует пользоваться для использования
этих формул без их запоминания.
Рис.
2.8
Правило 1. Перед приведенной функцией ставится тот знак, который имеет исходная функция в заданной четверти (квадранте), рис. 2.8.
Правило
2. Для углов (
)
или (
),
образованных откладыванием угла
от оси абсцисс (оси
),
формула приведения название
функции
не измененяет.
Для углов
(
)
или (
),
образованных откладыванием угла
от оси ординат (оси
),
формула приведения название
функции измененяет:
синус переходит в косинус (
),
косинус переходит в синус (
),
тангенс переходит в котангенс (
),
котангенс переходит в тангенс (
).
Правила приведения позволяют безошибочно и легко воспроизводить нужную формулу приведения. Все формулы приведения можно свести в одну таблицу 2.4. В практике удобно пользоваться два приведенных эмпирических правила, для этого их следует запомнить.
Таблица 2.4
Функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.9
Пример
2.8.
Вычислить
,
,
,
,
.
Решение.
1. Угол находится во второй четверти (рис. 2.9); из рисунка видно, что знак sin в этой четверти «+», значит у приведенной функции тоже будет знак «+».
П
Рис. 2.10
,
имеем дело со случаем
,
следовательно, меняем функцию с синуса
на косинус.
Имеем:
2.
Угол
находится в третьей четверти
(рис.
2.10), из рисунка видно, что знак sin
в этой
четверти равен «–», значит у приведенной
функции тоже будет знак «–».
Представим
как сумму
,
имеем дело со случаем
,
следовательно, функция не меняется.
Имеем:
3
Рис. 2.11
находится в четвертой четверти (рис.
2.11), из рисунка видно, что знак
в этой четверти равен
«+», значит у приведенной функции тоже
будет знак «+».
Представим
как сумму
,
имеем дело со случаем
,
следовательно, меняем функцию с косинуса
на синус.
И
Рис. 2.12
4.
Представим угол
,
тогда (рис.
2.12):
Угол находится во второй четверти; из рисунка видно, что знак в этой четверти «–», значит у приведенной функции тоже будет знак «–».
Представим
как сумму
,
имеем дело со случаем
,
следовательно, меняем функцию с косинуса
на синус.
И
Рис. 2.13
Представим
как сумму
(рис. 2.13).
Тогда
Пример
2.9.
Вычислить
,
.
Решение.
1
Рис. 2.14
в этой четверти «–»,
значит у приведенной функции тоже будет
знак «–».
Представим
как сумму
,
следовательно, меняем функцию с
на
.
И
Рис. 2.15
2. Угол находится в третьей четверти (рис. 2.15), из рисунка видно, что знак в этой четверти равен «+», значит у приведенной функции тоже будет знак «+».
Представим как сумму , следовательно, функция не меняется.
Имеем:
