
- •Министерство образования и науки рф Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования “Красноярский государственный педагогический университет
- •Тригонометрия Учебное пособие
- •© Красноярский государственный педагогический университет
- •§ 1. Основные понятия
- •1.1. Координатная плоскость
- •1.2. Углы и их измерение
- •§ 1.3. Тригонометрические функции угла
- •1.4. Радианная система измерения углов (дуг)
- •1.5. Аргумент тригонометрической функции
- •§ 2. Основные теоремы тригонометрии
- •2.1. Теорема синусов
- •2.3. Формулы приведения
- •2.4. Прикладные аспекты основных теорем тригонометрии
- •§ 3. Исследования тригонометрических функций
- •3. 1. Периодичность
- •§ 3. 2. Тригонометрические функции , , ,
- •§ 4. Тригонометрические уравнения
- •4.1. Простейшие тригонометрические уравнения
- •4.2. Общий случай тригонометрических уравнений
- •4.3. Понятие арксинуса, арккосинуса, арктангенса и арктангенса числа для записи корней тригонометрических уравнений
- •4.4. Тригонометрические уравнения, сводящиеся к простейшим
- •§ 5. Приложение тригонометрических функций
- •От аргумента в радианах
- •Тригонометрия
§ 2. Основные теоремы тригонометрии
2.1. Теорема синусов
Рис. 2. 1
В
плоском треугольнике со сторонами
![]() и углом
,
противолежащим стороне
(рис. 2.1), квадрат одной стороны треугольника
равен сумме квадратов двух других сторон
за вычетом удвоенного их произведения,
умноженного на косинус угла между ними,
т. е. справедливо равенство
и углом
,
противолежащим стороне
(рис. 2.1), квадрат одной стороны треугольника
равен сумме квадратов двух других сторон
за вычетом удвоенного их произведения,
умноженного на косинус угла между ними,
т. е. справедливо равенство
![]() .
.
Доказательство.
Рассмотрим
![]() .
Из вершины C
на сторону AB
опустим высоту CD.
Треугольник ADC является прямоугольным,
поэтому величину стороны AD можно
вычислить из соотношения тригонометрических
функций :
.
Из вершины C
на сторону AB
опустим высоту CD.
Треугольник ADC является прямоугольным,
поэтому величину стороны AD можно
вычислить из соотношения тригонометрических
функций :
![]() .
(а)
.
(а)
Длину стороны BD вычислим как разность AB и AD:
![]() .
(б)
.
(б)
Вычислим
по теореме Пифагора высоту
![]() .
.
Имеем
 Откуда
Откуда
![]() .
.
Подставим в последнее выражение вычисленные значения (а) и (б), получим
![]() .
.
Раскроим
скобки
![]() ,
,
и приведем подобные члены, получим
![]() . (1)
. (1)
Теорема доказана.
П
Рис. 2. 2
![]() ,
если
,
если
![]() ,
,
![]() ,
угол между сторонами равен
(рис. 2.2).
,
угол между сторонами равен
(рис. 2.2).
Решение. По теореме косинусов
![]()

Здесь по теореме приведения
 .
.
Полезно эту задачу решить геометрически, т.е. построить заданный треугольник в масштабе и измерить сторону . Полученные результаты сравнить.
П
Рис. 2. 3
![]() ;
;
![]() ;
;
![]() (рис. 2.3).
(рис. 2.3).
Решение. Опустим из вершины на основание высоту . Площадь треугольника будет равна
![]() .
.
По теореме косинусов
![]()
или
![]() .
.
Отсюда имеем:
 ;
;
![]() ;
;
![]() .
.
![]() .
.
Теорема синусов
Рассмотрим
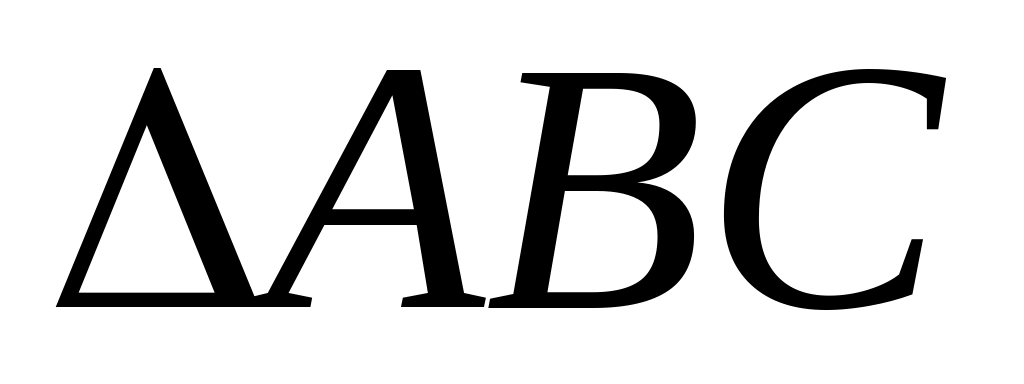 ,
описанный
вокруг треугольника окружности радиуса
;
a,
b, c
– стороны треугольника; α,
β, γ
– величины противолежащих этим сторонам
углов (рис. 2.4).
,
описанный
вокруг треугольника окружности радиуса
;
a,
b, c
– стороны треугольника; α,
β, γ
– величины противолежащих этим сторонам
углов (рис. 2.4).
Т

Рис. 2. 4
еорема. Стороны треугольника ABC пропорциональны синусам противолежащих углов:
 ,
где
R
– радиус описанной вокруг треугольника
окружности; a,
b, c
– стороны треугольника; α,
β, γ
– величины противолежащих этим сторонам
углов.
,
где
R
– радиус описанной вокруг треугольника
окружности; a,
b, c
– стороны треугольника; α,
β, γ
– величины противолежащих этим сторонам
углов.
Доказательство. Рассмотрим
произвольный треугольник, вписанный в
окружность, обозначим его как ABC (рис.
2.4). Для доказательства всей теоремы,
поскольку размеры треугольника выбраны
произвольным образом, достаточно
доказать, что соотношение одной
произвольной стороны к противолежащему
ей углу равно 2R, например,
 .
.
П
Рис. 2. 5
![]() равен углу
равен углу
![]() .
.
Из
![]()
![]()
![]() .
.
Повторив то же рассуждение для двух других сторон треугольника, получаем:
. Теорема доказана.
Если точки A и D лежат по разные
стороны от прямой BC (рис. 2.5), то угол
CDB равен углу
![]() .
Поскольку
.
Поскольку
![]() ,
то указанные варианты построения
треугольника все равно приведут к одному
результату.
,
то указанные варианты построения
треугольника все равно приведут к одному
результату.
Теорема
сложения для косинуса.
При произвольных
значениях
и
![]() имеют место теоремы сложения:
имеют место теоремы сложения:
![]() ;
;
Рис. 2. 6![]()

Доказательство.
Пусть
точки
![]() и
–
точки единичной окружности (рис. 2.6).
Запишем координаты точек
и
:
и
–
точки единичной окружности (рис. 2.6).
Запишем координаты точек
и
:

Вычислим квадрат расстояния между точками и
 (1)
(1)
Рассмотрим
разность дуг
и
– это
![]() ,
измеряющаяся числом
,
измеряющаяся числом
![]() .
Отложим
от начальной точки
.
Отложим
от начальной точки
![]() .
Пусть
.
Пусть
![]() – конец отложенной, т.е. дуги
=
.
Хорды
и
,
соединяющие концы равных дуг
и
,
равны между собой, т. е.
=
.
– конец отложенной, т.е. дуги
=
.
Хорды
и
,
соединяющие концы равных дуг
и
,
равны между собой, т. е.
=
.
Запишем координаты точки :
![]()
Вычислим квадрат расстояния между точками и :
 (2)
(2)
Приравняем правые части уравнений (1) и (2) между собой, получим
![]() ,
,
откуда
. (3)
Заменив
на
![]() в формуле (3), получим
в формуле (3), получим
. (4)
Теорема доказана.
Следствие
1.
Подставляя
в (4)
![]() ,
получим формулу косинуса двойного угла:
,
получим формулу косинуса двойного угла:
![]() .
.
Эта формула позволяет
Заменить выражение
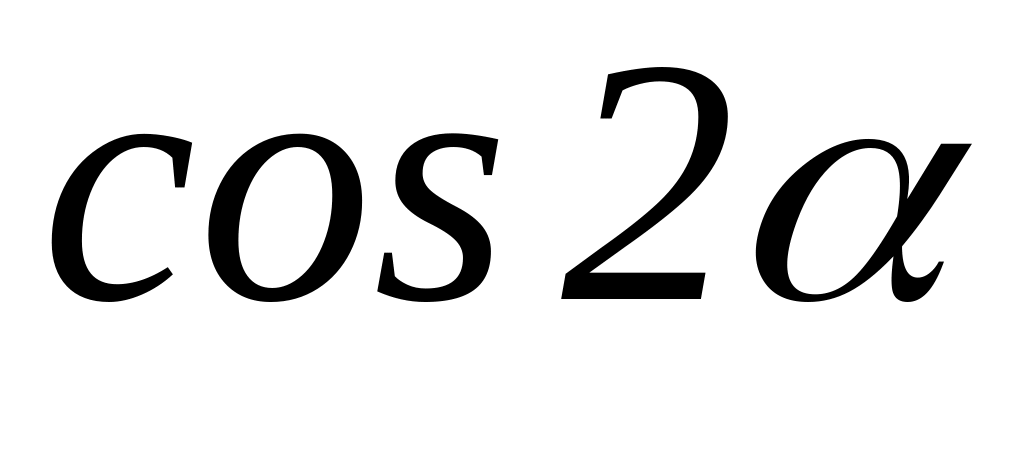 тождественно равным ему выражением
тождественно равным ему выражением
 ,
зависящим от
,
зависящим от
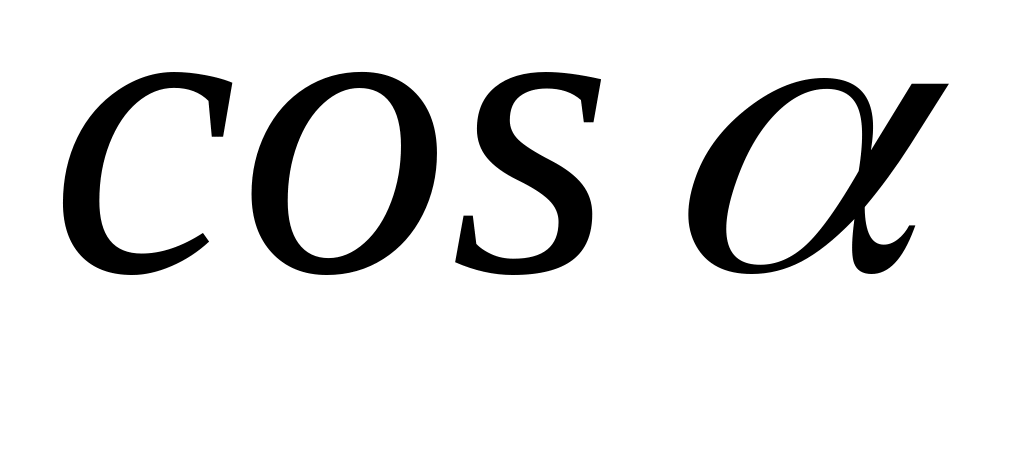 и
и
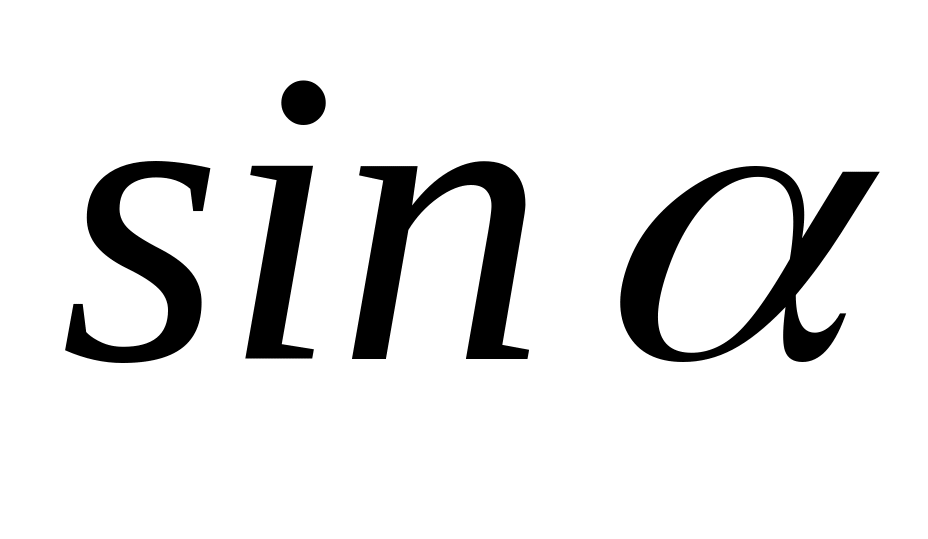 .
.Разложить на два множителя по примеру формулы сокращенного умножения
 :
:
3. Заменить выражение равным ему выражением .
Следствие 1. Используя основное тригонометрическое тождество
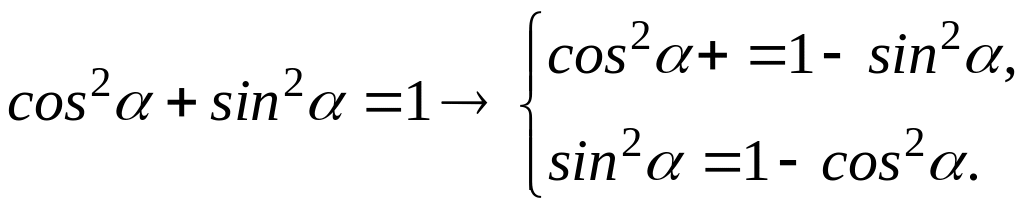
Получим другие варианты формулы двойного угла
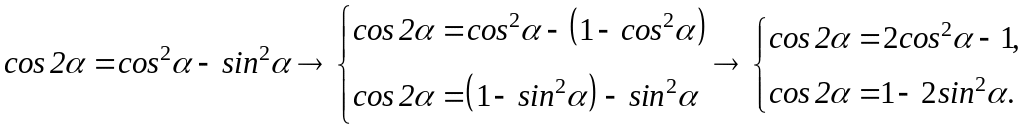
Пример
2.3.
Вычислить
![]() .
.
Решение.
Представим
угол
в виде разности
![]() .
Тогда
.
Тогда
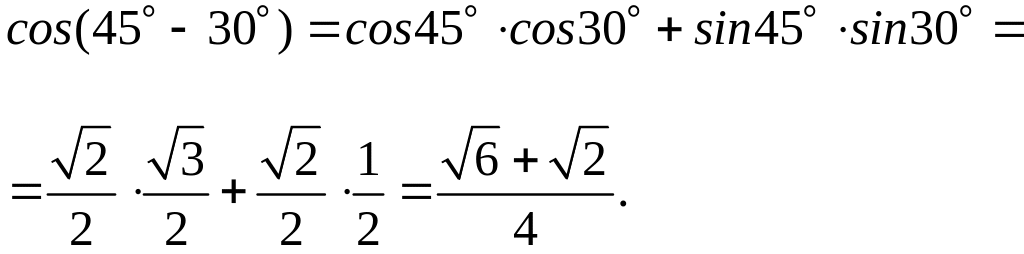
Пример
2.4.
Чему равно
значение
![]() ?
?
Решение. Воспользуемся формулой (3), получим
![]()
![]()
