1.5. Аргумент тригонометрической функции

Соответствие между углами и значениями данной тригонометрической функции позволяет всякую тригонометрическую функцию рассматривать как функцию; значениями аргумента являются углы, а значениями – числа.

Если известна сторона правильного -угольника, вписанного в тригонометрический круг (круг единичного радиуса), то легко вычислить значения тригонометрических функций от угла.

Впишем в единичную окружность равносторонний треугольник так, чтобы начальный радиус, лежащий на оси , поделил основание вписанного треугольника пополам (рис. 1.14). Тогда – синус угла , – косинус угла . Рассмотрим . Из геометрии известно, что катет, лежащий против угла в , равен половине гипотенузы.

И

Рис. 1.14

меем

;

;

.

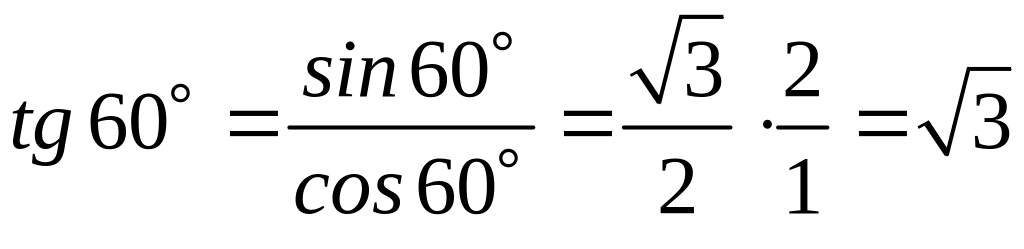В

Рис. 1.15

пишем в единичную окружность квадрат так, чтобы начальный радиус, лежащий на оси , поделил сторону вписанного квадрата пополам (рис. 1.15). Тогда – синус угла , – косинус угла . Рассмотрим равносторонний треугольник .

Имеем:

Рис. 1.16

Итак, получили, что

,

, .

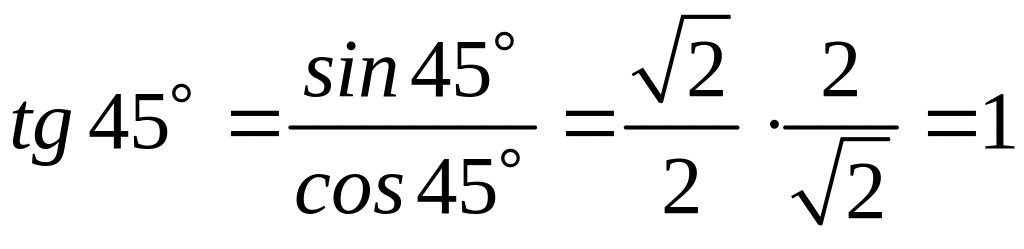Впишем в единичную окружность шестиугольник так, чтобы начальный радиус, лежащий на оси , поделил сторону вписанного шестиугольника пополам (рис. 1.16). Тогда – синус угла , – косинус угла . Рассмотрим . Из геометрии известно, что катет, лежащий против угла в , равен половине гипотенузы.

Имеем

.

,

.

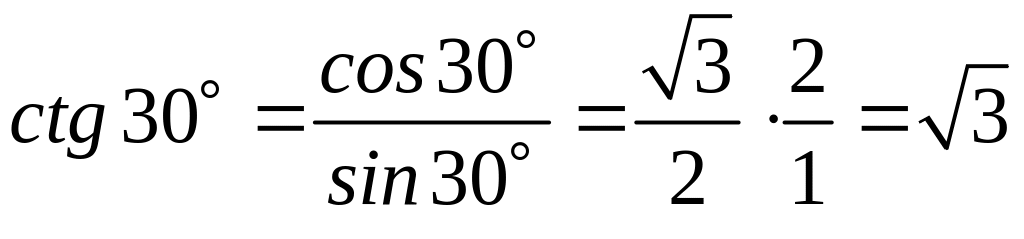Обобщим полученный результат. Пусть начальный радиус, лежащий на оси , делит пополам сторону вписанного -угольника, сторона которого равна , а угол между сторонами правильного многоугольника равен , рис. 1.16’.
Рис. 1.16’	Тогда будет соответствовать синусу угла , а – его косинусу, т.е.

Значения тригонометрических функций для некоторых аргументов приведены в таблице 1.3.

Таблица 1.3

( градус)
(радиан)	0
	0				1
	1			0,5	0

Приведенные значения тригонометрических функций полезно запомнить.

Историческая справка. Значительный вклад в становление теории тригонометрических функций внесли арабские ученые. Достижением арабских ученых является то, что они отделили тригонометрию от астрономии. В первом тысячелетии н.э. происходит бурный расцвет культуры и науки в странах Арабского Халифата, и основные открытия тригонометрии принадлежат ученым этих стран.

О

Рис. 1.17

писывая положение звезд, ученые этих стран в 4-5 в. пользовались лучом (длина луча соответствовала 1 масштабу), который направляли на звезду. В трудах по астрономии индийского учёного Ариабхаты отрезок CB (рис. 1.17) назван “ардхаджива” (“ардха” – половина, “джива” – тетива лука, которая напоминает хорду). При переводе арабских математических текстов слово “ардхаджива” было заменено латинским словом “синус” (sinus – изгиб, кривизна).

Косинус – это сокращение латинского выражения “completely sinus”, т.е. дополнительный синус (или иначе  синус дополнительной дуги).

Туркменский ученый аль-Маразви первым из известных нам исследователей ввел понятие тригонометрических функций как отношение сторон прямоугольного треугольника (рис. 1.18) и составил таблицы синусов, тангенсов и котангенсов:

Рис. 1.18

Значительных высот достигла тригонометрия и у индийских средневековых астрономов, достижением которых стала замена хорд синусами, что позволило вводить различные функции. В Индии было положено начало тригонометрии как учению о тригонометрических величинах.