1.4. Радианная система измерения углов (дуг)

Познакомимся с другой системой измерения углов (или дуг) – радианом. Проведем простой эксперимент. Выберем окружность, диаметр которой равен . Возьмем нерастяжимую нить (сантиметр), обмотаем ей окружность и измерим нитью длину этой окружности, пусть она равна ; наложим расправленную нерастяжимую нить на линейку и получим значение длины окружности – . Вычислим дробь, числитель которой равен длине окружности, знаменатель – диаметру:

.

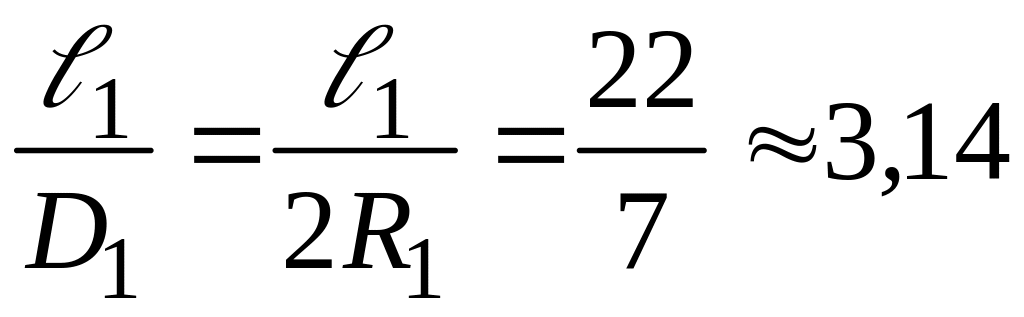Выберем другую окружность, диаметр которой равен , и повторим процедуру – нерастяжимой нитью измерим длину окружности, получим . Вычислим:

.

Выбирая пять окружностей любого диаметра и вычисляя дробь, числитель которой равен длине соответствующей окружности , знаменатель – ее диаметру , составим таблицу 1.1.

Таблица 1.1

– длина окружности (см)	75	27	31,2	15,7	55
– диаметр окружности (см)	23,9	8,6	9,9	5	17,5
	3,138	3,139	3,151	3,14	3,143
Среднее =

Из нашего эксперимента видно, что всегда получается примерно одно и то же число, равное , которое обозначается греческой буквой (читается «пи»):

^.

^{Отсюда длина окружности равна}

.

Правило. Отношение длины окружности к диаметру этой окружности есть постоянное число ( ), равное .

Число называют иррациональным числом. Более точные вычисления позволяют вычислить число с любой точностью:

Из геометрии известно, что отношение длины дуги , на которую опирается центральный угол, к радиусу этой окружности не зависит от самого радиуса: 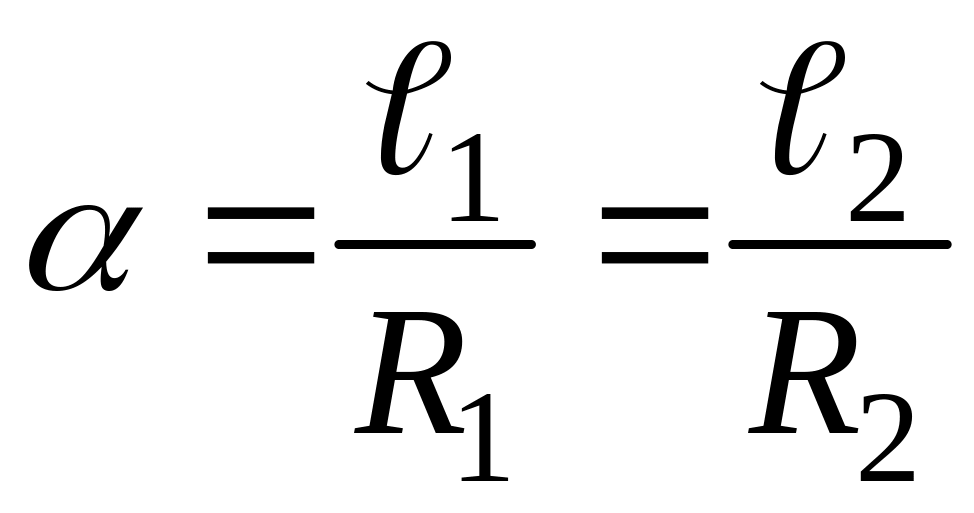, рис. 1.6, а. Поэтому отношение может быть выбрано характеристикой и мерой данного угла.

Определение: радианом называется величина внутреннего угла, который опирается на дугу окружности длиной в один радиус (обозначается 1 рад.)

Т

Рис. 1.11

акая мера называется радианной мерой угла и используется наравне с угловой (рис.1.11, б).

Определим геометрически, из скольких дуг длиной состоит окружность. Напомним, что отрезок , который соединяет какие-либо две точки окружности, называется хордой.

Вычислим аналитически, из скольких дуг длиной состоит окружность. Имеем:

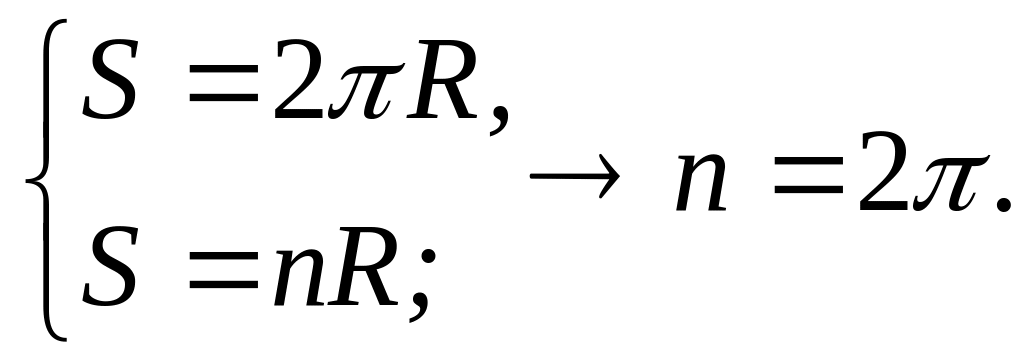
Поскольку вся окружность содержит , следовательно,

_{Вычислим, сколько градусов содержится в 1 радиане:}

Итак, .

В

Рис. 1.12

ычислим геометрически, из скольких дуг длиной состоит окружность. Для этого вычислим хорду , рис. 1.12. Рассмотрим равносторонний треугольник . Имеем:

.

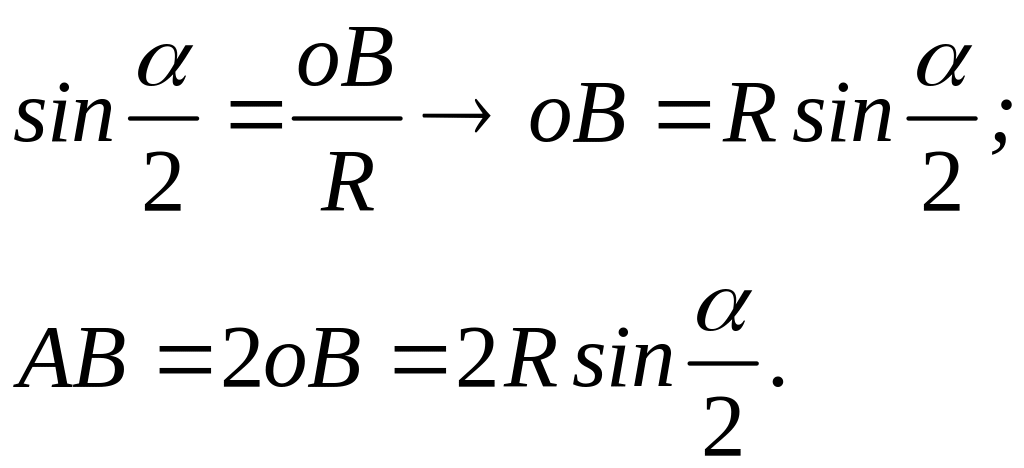Итак,

Откладывая циркулем хорды , как на рис. 1.12, мы видим, что на окружности укладывается хорд или дуг, длина которых равна .

Сравним геометрический и аналитический расчеты:

Правило. 1 радиан – это центральный угол, длина дуги которого равна радиусу окружности; радиан – .

Отметим, что при обозначении радианной меры не принято ставить единицы измерения.

_{Переход от градусной меры в радианную меру. Переход от градусной меры в радианную меру определен пропорцией}

Принято соотносить градусную меру измерения и радианную между собой.

В таблице 1.2 приведены численные значения перехода от градусной меры в радианную часто встречающихся углов по формуле:

.

Таблица 1.2

Угол	Радиан	Угол	Радиан
0	0

Приведенные в таблице значения полезно запомнить.

Сопоставим изображения действительных чисел точками на окружности и точками на прямой линии (оси ) при помощи следующего простого эксперимента (рис. 1.13, а, б).

Возьмем сантиметр (нерастяжимую нить), намотаем его на тригонометрическую окружность, радиус которой , совместив начало сантиметра с начальной точкой окружности, и отметим на нем соответствующие длины дуг; затем совместим начало сантиметра с начальной точкой числовой оси ; точки числовой прямой (на сантиметре) и точки пересечения соответствующего луча с окружностью, изображающие одно и то же число, совместятся.

Рис. 1.13

Правило Введение в рассмотрение углов любой величины позволяет поставить во взаимно однозначное соответствие множество всех действительных чисел и множество всех углов на плоскости; тогда всякому действительному числу соответствует некоторый угол ориентированной плоскости, и обратно – всякому углу соответствует некоторое действительное число.