§ 1.3. Тригонометрические функции угла

П

Рис. 1.6

усть задан луч , длина которого равна . Совместим декартовую систему координат с началом данного луча (рис. 1.6). Тогда луч образует с осью угол . Определим проекции луча на оси Оx и . Для этого опустим перпендикуляры из точи к декартовым осям Ох и Оу. Проекции луча на ось Ох и Оy соответствуют отрезкам и .

Свяжем длину луча с проекциями и . Рассмотрим , сторонами которого являются проекции луча – и (рис. 1). По теореме Пифагора имеем

.

Теорема. Для произвольного луча а, образующего угол с осью , отношения и не зависят от длины луча и определяются углом .

Д

Рис. 1.7

оказательство. Проведем линию , образующую угол с положительным направлением оси в декартовой системе координат (рис. 1.7). Отложим на этой линии точку А, длина которой равна а. Проекция точки А на ось Ох соответствует отрезку , проекция точки А на ось – . Отложим на линии две произвольные точки и . Опустим из этих точек перпендикуляры на ось , получим координаты этих точек: и , соответственно. Рассмотрим треугольники , и . Эти треугольники подобны: ~ ~ .

С Рис. 1.8 правка. Преобразованием подобия называется преобразование, при котором расстояние между любыми двумя точками изменяется в одно и то же число раз. Это значит, что если произвольные точки фигуры при преобразовании подобия переходят в точки фигуры , то , где – постоянное число и называется коэффициентом подобия. Преобразование подобия – взаимно однозначное преобразование. Фигура называется подобной фигуре с коэффициентом . Подобие фигур обозначается знаком «~»; это означает, что фигура подобна фигуре , т.е. ~ (рис. 1.8).

Из подобия треугольников запишем отношение катетов к гипотенузам соответствующих треугольников (рис. 1.7). Имеем:

и . (1)

Равенство (1) выражает отношение сходственных катетов к гипотенузе и показывает, что отношение сходственных катетов к гипотенузе при заданном угле одно и то же, независимо от длины отрезка а.

Аналогично имеем, что отношение катетов между собой при заданном угле одно и то же, не зависит от длины отрезка а:

. (2)

Из соотношений (1) и (2) можно сделать вывод, что в любом прямоугольном треугольнике отношения катетов к гипотенузе и отношения катетов между собой определяются только заданным углом , который образует гипотенуза с осью и не зависит от длины гипотенузы этого треугольника (рис. 1.7). Поэтому эти отношения являются своеобразными характеристиками угла .

Р

Рис. 1.9

ассмотрим прямоугольный треугольник , где ﮮ – прямой (рис. 1.9). Будем называть катет прилежащим, а катет – противолежащим.

На основании выражений (1) и (2) сформулируем тригонометрические функции угла .

Определения тригонометрических функций угла

1. Отношение противолежащего катета к гипотенузе 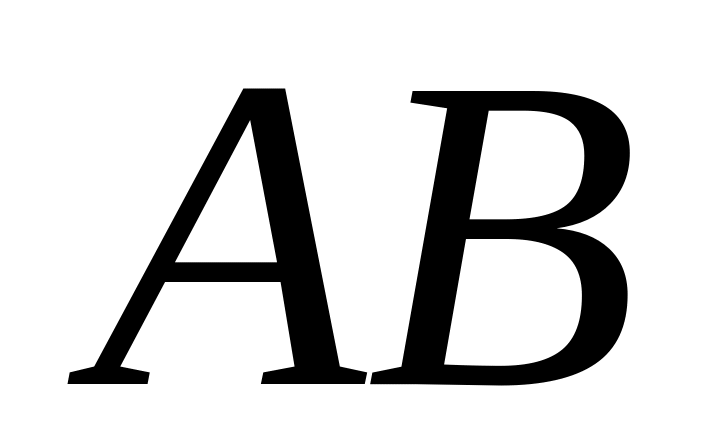называется синусом угла и обозначается :

.

2. Отношение прилежащего катета к гипотенузе называется косинусом угла и обозначается :

.

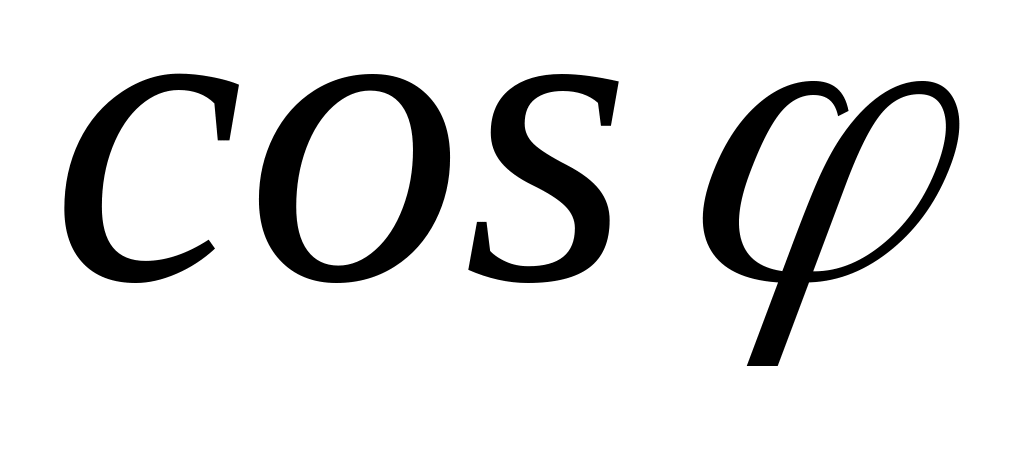3. Отношение противолежащего катета к прилежащему катету называется тангенсом угла и обозначается :

.

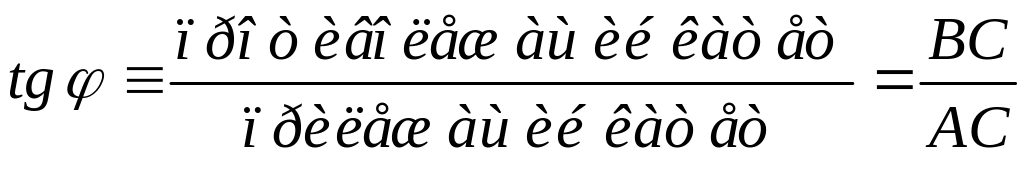4. Отношение прилежащего катета к противолежащему катету называется котангенсом угла и обозначается :

.

Полученные соотношения называются тригонометрическими функциями угла .

К

Рис. 1.10

аждое из этих отношений определяется только углом и не зависит от величины гипотенузы, поэтому имеет смысл ввести прямоугольный треугольник с гипотенузой, равной единице. Тогда концы всех лучей, равные по длине гипотенузе, расположатся на окружности, радиус которой равен 1 (единичной окружности), и множество прямоугольников с гипотенузой, равной 1, будут вписаны в эту окружность (рис. 1.10). Этот круг вводится для исследования тригонометрических функций. Поэтому он получил специальное название – тригонометрический круг или круг единичного радиуса.

В физике, механике, технике существует потребность в необходимости дальнейшего расширения понятия угла. В кинематической интерпретации полный угол соответствует «пути», пройденном лучом, вращающимся в плоскости вокруг центра , который, описав в плоскости полный оборот (в положительном или отрицательном направлении), вернулся в первоначальное положение.

Винт, пропеллер на самолете, маховое колесо, карусель и т. д. могут совершать любое количество полных оборотов в любом направлении. Исходя из этого, считают, что всякое действительное число взаимно однозначно определяет некоторый угол в радианах. Пусть – данное положительное число; если , то это число определяет тот угол, который им измеряется; если , то угол представляется в виде суммы

,

где , а – целое положительное число. Тогда рассматриваем угол, определяемый числом , как состоящий из положительных полных углов и угла .

Аналогично, если – отрицательное число и , то можно представить в том же виде: , где , а – целое отрицательное число.