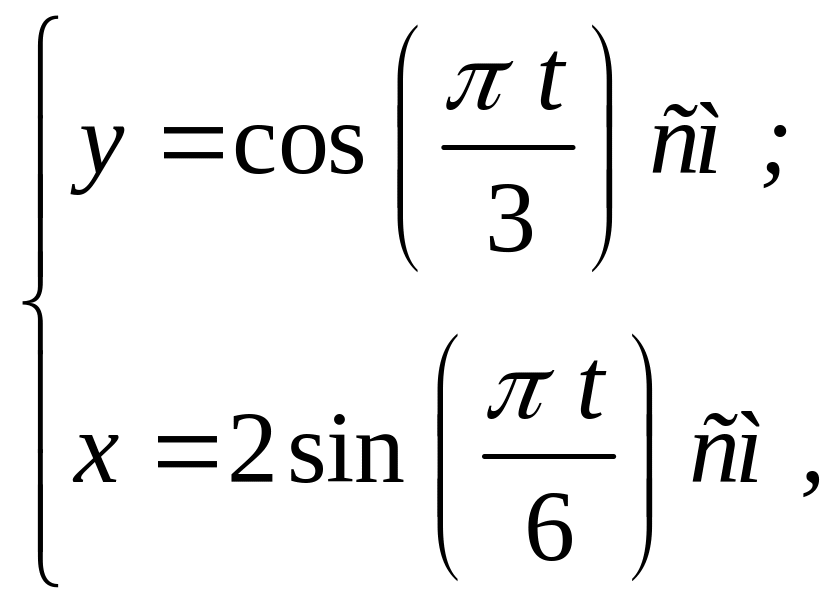- •Министерство образования и науки рф Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования “Красноярский государственный педагогический университет
- •Тригонометрия Учебное пособие
- •© Красноярский государственный педагогический университет
- •§ 1. Основные понятия
- •1.1. Координатная плоскость
- •1.2. Углы и их измерение
- •§ 1.3. Тригонометрические функции угла
- •1.4. Радианная система измерения углов (дуг)
- •1.5. Аргумент тригонометрической функции
- •§ 2. Основные теоремы тригонометрии
- •2.1. Теорема синусов
- •2.3. Формулы приведения
- •2.4. Прикладные аспекты основных теорем тригонометрии
- •§ 3. Исследования тригонометрических функций
- •3. 1. Периодичность
- •§ 3. 2. Тригонометрические функции , , ,
- •§ 4. Тригонометрические уравнения
- •4.1. Простейшие тригонометрические уравнения
- •4.2. Общий случай тригонометрических уравнений
- •4.3. Понятие арксинуса, арккосинуса, арктангенса и арктангенса числа для записи корней тригонометрических уравнений
- •4.4. Тригонометрические уравнения, сводящиеся к простейшим
- •§ 5. Приложение тригонометрических функций
- •От аргумента в радианах
- •Тригонометрия
§ 5. Приложение тригонометрических функций
В физике, механике, технике, химии, биологии и др. науках изучаются периодические движения, или колебания. Колебания – такие изменения состояния исследуемой системы или объекта наблюдения, которые характеризуются определенной степенью повторяемости во времени, возвращаемости к начальному состоянию. Периодом колебаний называется промежуток времени, в течение которого совершается одно полное движение. Следовательно, для описания периодических процессов следует вводить функции, зависящие от времени, т. е. параметра (время).
Пусть
периодические движения проходят вдоль
одного выделенного направления, например,
вдоль оси
декартовой системы координат,
следовательно, координата
должна зависеть от
,
т. е. задается функция
![]() .
Если периодические движения проходит
в плоскости
декартовой системы координат, тогда
задаются две функции:
и
.
Если периодические движения проходит
в плоскости
декартовой системы координат, тогда
задаются две функции:
и
![]() .
.
Рассмотрим примеры их механики.
Определение траектории движения
точки. Геометрическое место
последовательных положений при движении
точки в интервале времени
![]() в выбранной системе координат
евклидового пространства называется
траекторией движущейся точки.
Если в интервале времени
траектория прямая линия, то движение
в этом интервале называется прямолинейным,
в противном случае – движение называется
криволинейным.
в выбранной системе координат
евклидового пространства называется
траекторией движущейся точки.
Если в интервале времени
траектория прямая линия, то движение
в этом интервале называется прямолинейным,
в противном случае – движение называется
криволинейным.
В частности, движение точки на интервале времени называют круговым, если на этом интервале точка движется по окружности.
Пример 5.1. Точка движется по оси . Уравнение движения точки задано уравнением
![]() .
(а)
.
(а)
Определить траекторию движения точки.
Провести анализ движения точки по заданной траектории.
3. Вычислить среднюю скорость точки
в
промежутке времени
![]()
Решение.
Определим траекторию движения точки.
Для этого в декартовой системе координат определим область, в которой движется точка, т.е. область значений заданной функции .
Введем обозначение:
![]() ,
тогда уравнение (а) будет иметь вид
,
тогда уравнение (а) будет иметь вид
![]() .
.
Функции
ограничена, т.е.
![]() ,
следовательно
,
следовательно
![]() .
.
Итак,
функция
![]() определена в пределах (рис. 5.1, а)
определена в пределах (рис. 5.1, а)
![]() .
.
Построим график заданной
функции
в системе координат
![]() ,
здесь
– абсолютное время, причем
,
здесь
– абсолютное время, причем
![]() ,
рис.5.1,а. Графиком этой функции является
синусоида,
,
рис.5.1,а. Графиком этой функции является
синусоида,
![]() .
При
.
При
![]() функция
функция
![]() возрастает до
возрастает до
![]() ,
далее при
,
далее при
![]() функция убывает до
функция убывает до
![]() ,
при
,
при
![]() функция возрастает до
функция возрастает до
![]() .
Период функции
.
Период функции
![]() .
.
Точка движется в евклидовом
пространстве
.
Графиком заданной функции является
отрезок
![]() ,
который и является
траекторией движения
точки
(рис. 5.1, б).
,
который и является
траекторией движения
точки
(рис. 5.1, б).

Рис. 5.1
Проведем анализ движения точки по заданной траектории в евклидовом пространстве :
1. При
![]() точка
точка
![]() начинает движение вправо из положения
начинает движение вправо из положения
![]()
![]() .
.
2. При
![]() точка
из положения
точка
из положения
![]() движется вправо, проходит
движется вправо, проходит
![]() до точки
до точки
![]() и останавливается.
и останавливается.
3. При
![]() начинает движение влево, проходя
положение
начинает движение влево, проходя
положение
![]() ,
и останавливается в точке
,
и останавливается в точке
![]() .
.
4. При
![]() точка движется вправо и т. д. Движение
повторяется до бесконечности.
точка движется вправо и т. д. Движение
повторяется до бесконечности.
За
![]() точка
возвращается в исходное положение,
следовательно, период движения
точка
возвращается в исходное положение,
следовательно, период движения
![]() Нетрудно видеть (рис. 5.1, а), что при
Нетрудно видеть (рис. 5.1, а), что при
![]() где
где
![]() точка
будет находиться в положении
,
при
точка
будет находиться в положении
,
при
![]() точка
будет занимать положение
точка
будет занимать положение
![]() ,
при
,
при
![]() –
–
![]() .
.
Итак, траекторией движения точки является отрезок , на котором она совершает периодическое движение с периодом
Вычислим среднюю скорость точки в промежутке времени

Вычислим среднюю скорость точки . Составим таблицу 5.1 значений и построим график зависимости координаты от времени по точкам (рис. 5.2).
Таблица 5.1
Р |
|
Вычислим среднюю скорость точки
в промежутке времени
![]()
 .
.
П
Рис. 4.4 Рис.
5.3
Рис.
5.3![]() (рад). Определить траекторию движения
точек
и
и вычислить среднюю скорость точки
в промежутке времени
(рад). Определить траекторию движения
точек
и
и вычислить среднюю скорость точки
в промежутке времени
![]() ,
если
,
если
![]() м.
м.
Решение. Декартовую систему
координат
![]() совместим с точкой О кривошипа
0А (рис. 5.3). Движение каждой
точки данного механизма можно задать
координатным способом относительно
выбранной системы отсчета, т.е. задать
координаты
совместим с точкой О кривошипа
0А (рис. 5.3). Движение каждой
точки данного механизма можно задать
координатным способом относительно
выбранной системы отсчета, т.е. задать
координаты
![]() и
и
![]() каждой точки.
каждой точки.
I. Определим траекторию
точки А. Положение точки А
определяется координатами
![]() :
:
 (а)
(а)
Д
Рис. 4.4 Рис.
5.4
Рис.
5.4![]() и
и
![]() .
Функции
.
Функции
![]() и
и
![]() ограничены, тогда область значений
ограничены, тогда область значений
![]() и
и
![]() определяется неравенствами:
определяется неравенствами:
 (б)
(б)
Тем самым определили область, в которой точка движется (рис. 5.4).
Получим аналитическую функцию, которая является траекторией точки. Для этого исключим параметр t из уравнений движения (a). Для этого возводим в квадрат каждое уравнение (а) и сложим их между собой.
Имеем:
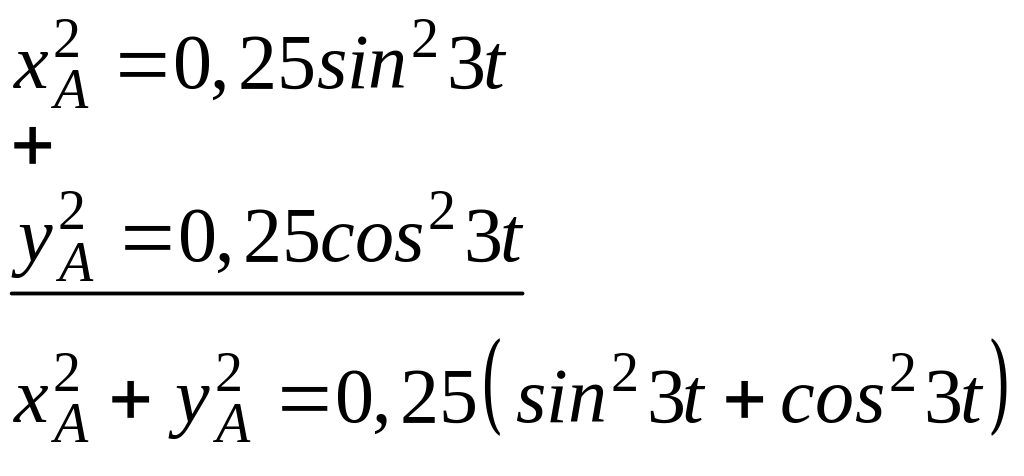
Учитывая,
что
![]() ,
получим:
,
получим:
![]() .
.
Итак, точка
движется по окружности радиуса
![]() м.
м.
С |
Построим графики функций
![]() и
и
![]() в системах координат
и
в системах координат
и
![]() ,
соответственно (рис. 5.5). Здесь
– абсолютное время, причем
.
Вычислим положение точки А при
сек. Имеем
,
соответственно (рис. 5.5). Здесь
– абсолютное время, причем
.
Вычислим положение точки А при
сек. Имеем


Рис. 5.5
Опишем движение точки А:
1. При
точка
![]() при имеет координаты
при имеет координаты
![]() .
.
2. При
![]() функция
убывает, а функция
функция
убывает, а функция
![]() возрастает, следовательно, точка от
положения
возрастает, следовательно, точка от
положения
![]() начинает движение по окружности против
часовой стрелки (рис. 5.4). Период движения
начинает движение по окружности против
часовой стрелки (рис. 5.4). Период движения
![]()
Вычислим среднюю скорость точки
в период
![]() .
.
Вычислим числовые значения (рис. 5.6):
![]() .
.



Рис. 5.6
Тогда:
 ,
,
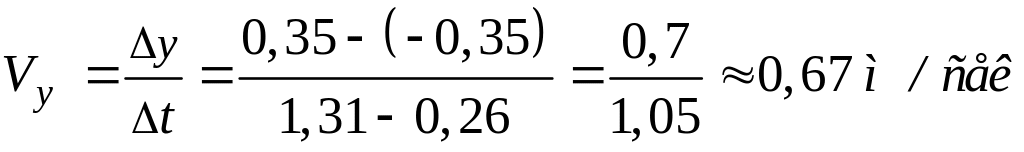 ,
,
![]() .
.
II. Определим траекторию
точки B. Уравнение
движения точки В в
системе координат
определено координатой
![]() (рис. 5.7, а):
(рис. 5.7, а):
![]() .
.
Для
построения траектории
в декартовой системе координат
![]() определим область значений
определим область значений
![]() .
Функция
ограничена, тогда область значений
определяется неравенством (рис. 5.7, а):
.
Функция
ограничена, тогда область значений
определяется неравенством (рис. 5.7, а):
![]() (б)
(б)
Траекторией движения точки
является отрезок
![]() ,
рис. 5.7, а.
,
рис. 5.7, а.

Рис. 5.7
Проведем анализ движения
точки
по заданной траектории в евклидовом
пространстве
.
Точка В при
имеет координаты
![]() ,
рис. 5.7, б. Далее точка движется влево и
за
,
рис. 5.7, б. Далее точка движется влево и
за
![]() проходит положение
проходит положение
![]() и достигает положение
и достигает положение
![]() ,
далее возвращается в положение
.
Положение точки
в различные моменты времени показаны
в таблице 5.2.
,
далее возвращается в положение
.
Положение точки
в различные моменты времени показаны
в таблице 5.2.
Таблица 5.2
,сек |
0 |
|
|
|
|
|
1 |
0 |
-1 |
0 |
1 |
,сек |
|
|
|
|
|
|
1 |
0 |
-1 |
0 |
1 |
Движение повторяется до
бесконечности. От начала движения до
возвращения в исходное положение
проходит
![]() сек,
следовательно, период движения
сек,
следовательно, период движения
![]() ,
что составляет
,
что составляет
![]() сек.
сек.
Нетрудно видеть (рис. 5.6, б), что:
– при
![]() точка
занимает положение
точка
занимает положение
![]() ;
;
– при
![]() где
точка
занимает положение
где
точка
занимает положение
![]() ;
;
– при
![]() где
точка
занимает положение
;
где
точка
занимает положение
;
Итак, траекторией движения
точки
является отрезок
,
на котором она совершает периодической
движение с периодом
![]()
Пример 5.3. Движение точки M по плоскости Оху задано уравнениями движения
 (а)
(а)
Построить
траекторию движущейся точки, вычислить
среднюю скорость движения точки
по оси
и оси
в промежутке времени
![]() .
.
Решение. Движение точки задано параметрическими уравнениями, параметром является время .
Построим графики заданных функций в системах координат и , соответственно, здесь – абсолютное время, причем, всегда .
Графиком функции
![]() является синусоида с периодом
является синусоида с периодом
![]() сек
и
сек
и
![]() ,
рис. 5.8, а.
,
рис. 5.8, а.

Рис. 5.8
Проведем анализ движения
точки по оси
![]() :
:
– при
![]() функция
возрастает до
функция
возрастает до
![]() ;
;
– при
![]() функция убывает от
до
функция убывает от
до
![]() ;
;
– при
![]() функция возрастает от
до
,
то есть возвращается в исходное положение.
функция возрастает от
до
,
то есть возвращается в исходное положение.
Далее движение точки повторяется до бесконечности.
Графиком функции
![]() является косинусоида с
периодом
сек
и
является косинусоида с
периодом
сек
и
![]() (рис. 5.8, б).
(рис. 5.8, б).
Проведем анализ движения
точки по оси
![]() :
:
– при
![]() функция
убывает от
функция
убывает от
![]() до
до
![]() ;
;
–
Рис. 5.9![]() функция возрастает опять до
.
функция возрастает опять до
.
Т очка
движется в евклидовом пространстве
.
Для построения траектории движущейся
точки в декартовой системе координат
определим область, в которой движется
точка, т.е. область значений
очка
движется в евклидовом пространстве
.
Для построения траектории движущейся
точки в декартовой системе координат
определим область, в которой движется
точка, т.е. область значений
![]() и
и
![]() .
.
Функции
![]() и
и
![]() ограничены, т.е.
ограничены, т.е.
![]() ,
,
![]() ,
,
получаем (рис. 5.9):
![]()
Выделяем на плоскости область, ограниченную полученными неравенствами.
Тем самым мы определили область, в
которой точка движется. Получим
аналитическую функцию
![]() ,
которая является траекторией точки в
евклидовом пространстве
.
Для этого исключим из параметрических
уравнений параметр t:
,
которая является траекторией точки в
евклидовом пространстве
.
Для этого исключим из параметрических
уравнений параметр t:
(а’)
Для этого делим первое уравнение системы (а’) на 2, второе – на 4. Далее, возводим полученные выражения в квадрат и складываем их между собой:

Учитывая,
что
![]() ,
получим:
,
получим:
![]() . (б)
. (б)
Получили
каноническое уравнение эллипса. Итак,
траекторией движущейся точки является
эллипс (рис. 5.9). Подставляя в (а) значение
![]() ,
находим положение точки
при
:
,
находим положение точки
при
:
![]() ;
;
![]() см.
см.
Точка в начальный
момент времени занимает положение
![]() .
Определим направление движения точки.
Уравнения движения (а) заданы возрастающей
функцией
.
Определим направление движения точки.
Уравнения движения (а) заданы возрастающей
функцией
![]() и убывающей функцией
и убывающей функцией
![]() ,
поэтому при увеличении t
координата «х» возрастает, а «у»
убывает, следовательно, точка движется
по эллипсу по часовой стрелке с периодом
,
поэтому при увеличении t
координата «х» возрастает, а «у»
убывает, следовательно, точка движется
по эллипсу по часовой стрелке с периодом
![]() .
.
Справка. Каноническое уравнение эллипса имеет вид
г |
Пример 5.4.
Движение точки в
плоскости
![]() задано координатным способом уравнения
задано координатным способом уравнения
![]() ,
,
![]() :
:
|
(а) |
(б) |
где
![]() и
и
![]() выражены в см,
выражены в см,
![]()
в сек.
в сек.
Требуется задать движение
точки в явном виде; вычислить
скорость, нормальную и
касательную составляющие ускорения,
радиус кривизны траектории в соответствующей
точке для момента времени
![]() сек.
сек.
Решение. Для построения траектории в декартовой системе координат определим область значений и . Функции и ограничены, тогда область значений и определяется неравенствами:
 (в)
(в)
Получим зависимость
![]() .
Для этого из (а) и (б) исключим параметр
.
Для этого из (а) и (б) исключим параметр
![]() .
Введём обозначение
,
тогда уравнения (а) и (б) перепишутся в
виде:
.
Введём обозначение
,
тогда уравнения (а) и (б) перепишутся в
виде:

Распишем первое уравнение
полученной системы, используя формулу
двойного угла (![]() ),
и приведем подобные члены:
),
и приведем подобные члены:

Заменим
![]() ,
получим
,
получим
 .
.
Итак, координаты и декартовой системы координат связаны между собой зависимостью . Эта зависимость определяет траекторию движения точки в евклидовом пространстве, ограниченной системой неравенств (в). Итак, получили, что точка движется по параболе:
![]() ,
где
,
где
Рис. 5.10
Построим график полученной
функции. Вершина параболы находится в
точке
![]() ,
ветви параболы вытянуты вдоль оси
и
направлены вниз (рис. 5.10).
,
ветви параболы вытянуты вдоль оси
и
направлены вниз (рис. 5.10).
При
![]() функция
функция
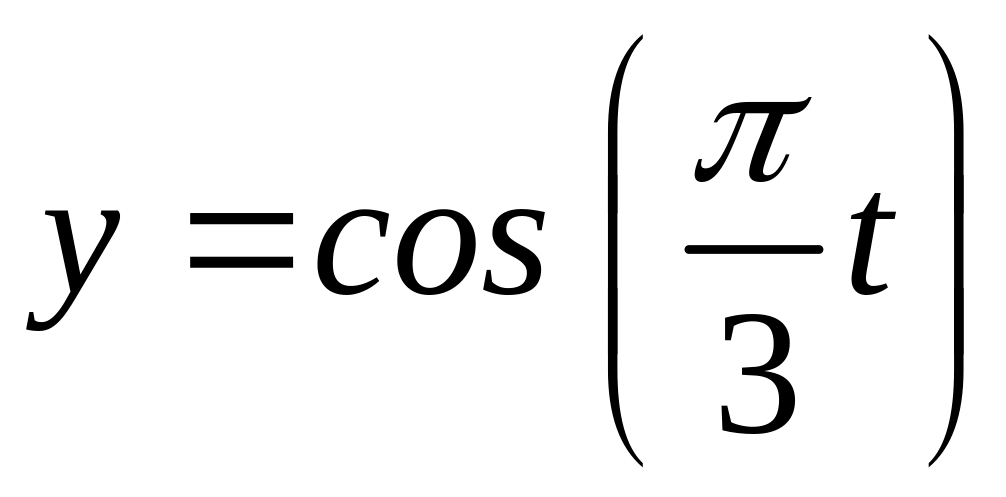 убывает, следовательно,
точка из положения
убывает, следовательно,
точка из положения
![]() начинает движение по правой ветви
параболы до точки
начинает движение по правой ветви
параболы до точки
![]() ,
далее точка движется обратно по верхней
ветви параболы и через точку с координатами
,
далее точка движется обратно по верхней
ветви параболы и через точку с координатами
![]() движется по нижней ветви параболы до
точки
движется по нижней ветви параболы до
точки
![]() и т.д.
и т.д.
В целом точка М совершает колебательные движения по параболе в ограниченной пунктиром области. Направление движения в первые 2 сек указано стрелкой на рис. 5.10.
Пример 5.5. Точка движется в плоскости . Уравнение движения точки задано координатным способом:
 (а)
(а)
где и выражены в см, в сек.
Требуется построить траекторию движения точки в декартовой системе координат.
Решение.
Построим траекторию
движения точки. Для
этого в декартовой
системе координат определим область,
в которой движется точка, т.е. область
значений
и
![]() .
Функции
и
ограничены, т.е.
,
.
Функции
и
ограничены, т.е.
,
![]() ,
получаем из (а), рис. 5.11:
,
получаем из (а), рис. 5.11:
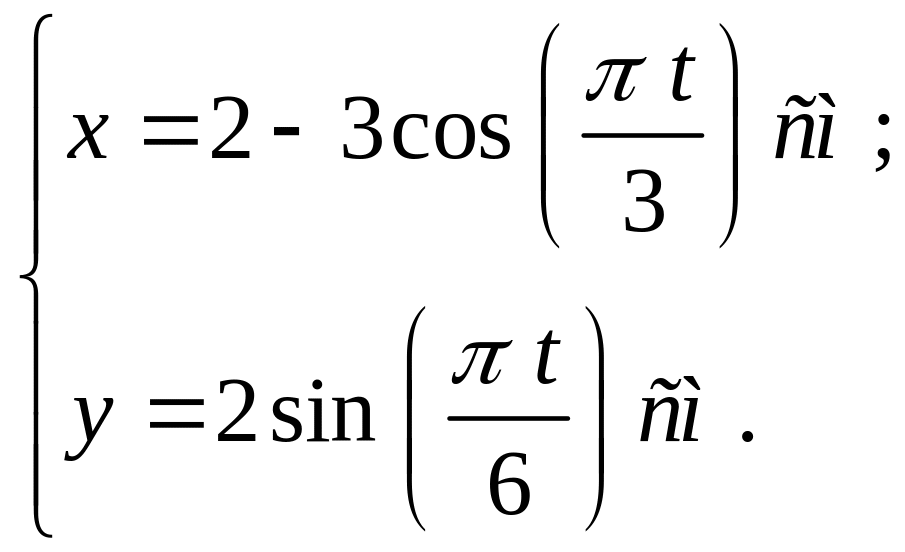

Получим уравнение траектории в системе
координат
евклидового пространства, т. е. зависимость
![]() .
Для этого из уравнений (а) исключим
параметр
.
Введём обозначение
.
Для этого из уравнений (а) исключим
параметр
.
Введём обозначение
![]() ,
тогда уравнения (а) перепишутся в виде
,
тогда уравнения (а) перепишутся в виде
 (б)
(б)
Распишем первое уравнение системы (б),
используя формулу двойного угла (![]() ),
),
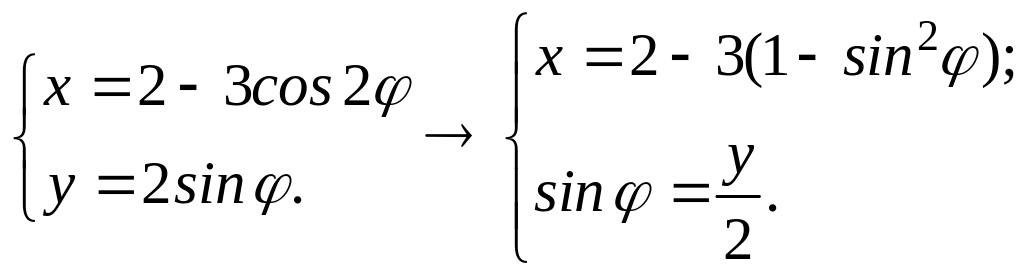
Получим:
Рис. 5.11

Уравнение траектории в системе координат евклидового пространства имеет вид
![]() ,
где
,
где
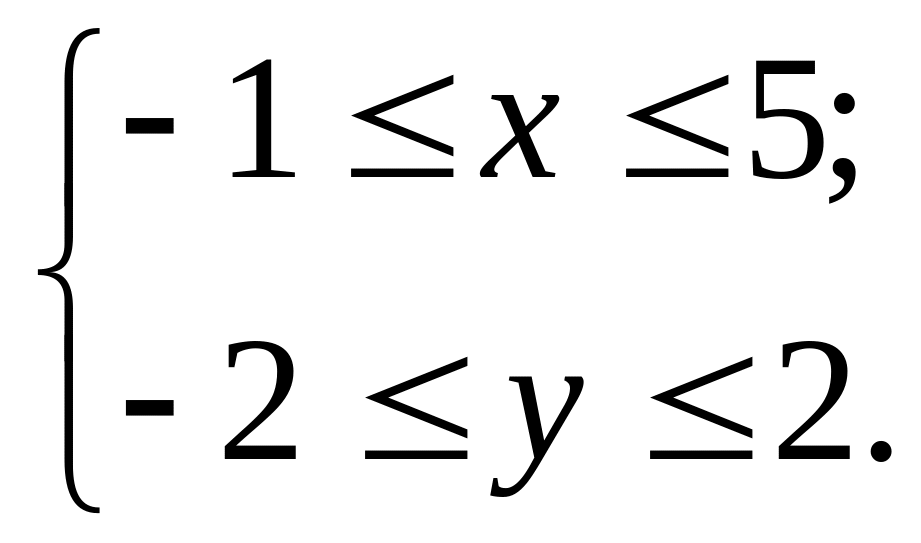 .
(с)
.
(с)
Траекторией точки является парабола,
вершина которой имеем координаты
![]() ;
ветви параболы вытянуты вдоль оси
;
ветви параболы вытянуты вдоль оси
![]() (рис. 5.11).
(рис. 5.11).
Проведем анализ движения точки по траектории. Вычислим положение точки на траектории в начальный момент времени (при ):

Положения точки в разные моменты времени приведены в таблице 5.3.
Таблица 5.3
Здесь
|
При
![]() функции
функции
![]() и
возрастают (рис. 5.11), точка М из
положения
и
возрастают (рис. 5.11), точка М из
положения
![]() начинает движение по верхней ветви
параболы до положения
начинает движение по верхней ветви
параболы до положения
![]() ;
далее при
;
далее при
![]() точка движется обратно по верхней
ветви траектории до точки
и при
точка движется обратно по верхней
ветви траектории до точки
и при
![]() продолжает движение по нижней ветви
параболы до положения
продолжает движение по нижней ветви
параболы до положения
![]() ,
далее при
,
далее при
![]() точка
возвращается в первоначальное положение
точка
возвращается в первоначальное положение
![]() ,
т.е. завершает цикл, далее движение
повторяется. Время одного цикла движения
,
т.е. завершает цикл, далее движение
повторяется. Время одного цикла движения
![]() Точка совершает колебательные движения
по параболе.
Точка совершает колебательные движения
по параболе.
Математический маятник. Для описания колебания маятников (рис. 5.12), вводится математическая модель – математический маятник, состоящий их материальной точки (тело, размерами которого можно пренебречь), расположенной на конце невесомого стержня длиной , свободно вращающегося вокруг оси, проходящей через его верхний конец. Как правило, задача состоит в том, чтобы вычислить частоту колебания маятника.
Рис. 5.12
![]() .
Маятник движется в плоскости
в среде без сопротивления, рис. 5.13. Для
малых отклонений маятника, т. е.
.
Маятник движется в плоскости
в среде без сопротивления, рис. 5.13. Для
малых отклонений маятника, т. е.
![]() ,
уравнение движения маятника задано
уравнением:
,
уравнение движения маятника задано
уравнением:
Рис. 5.13
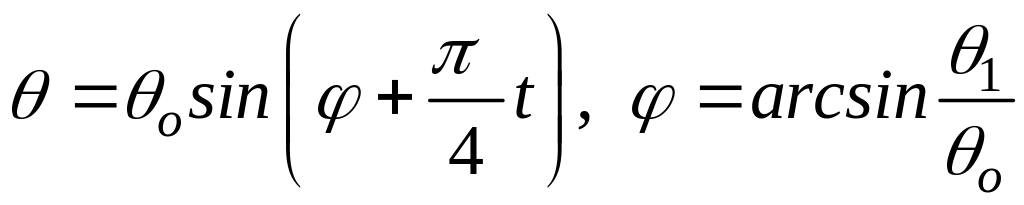 .
.
Здесь – постоянная движения, зависящая от величин:
1.
![]() – максимальная амплитуда колебаний.
– максимальная амплитуда колебаний.
2.
![]() – угол, при котором движение начинается
в момент времени
– угол, при котором движение начинается
в момент времени
![]()
Маятник может быть приведен
в движение из положения
![]() ,
тогда
,
тогда
 .
.
В этом случае уравнение движения маятника будет иметь вид
 .
.
Рассмотрим задачу при
![]() (
(![]() ).
Тогда маятник совершает колебательные
движения в пределах от
).
Тогда маятник совершает колебательные
движения в пределах от
![]() до
до
![]() .
В поворотных точках
и
.
В поворотных точках
и
![]() скорость маятника равна нулю.
скорость маятника равна нулю.
График зависимости
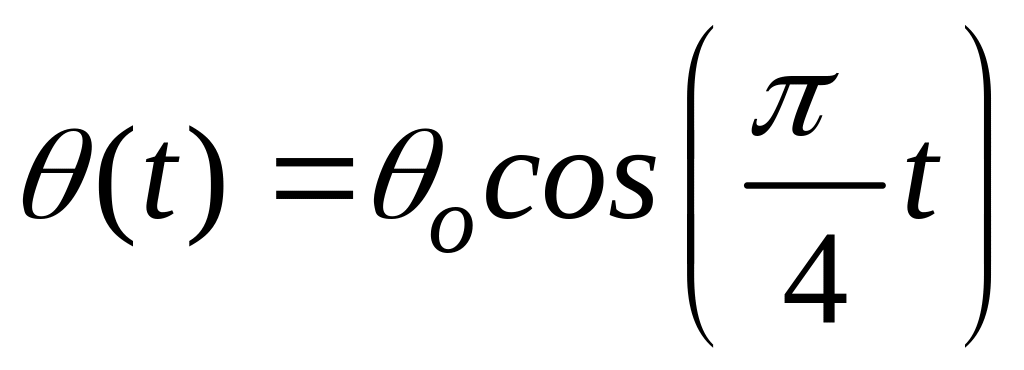 от
показан на рис. 5.14.
от
показан на рис. 5.14.

Рис. 5.14
Рис. 5.15
![]() имеем:
имеем:
![]()
Из теоремы Пифагора (рис. 5.15) вычислим:

Здесь:
![]() .
.
Существует легенда, что Галилей, стоя на молитве в соборе, внимательно наблюдал за качением бронзовых люстр. Он наблюдал и определял время, затраченное люстрой на движение туда и обратно. Это время потом назвали периодом колебаний. Часов у Галилея не было, и, чтобы сравнить период колебаний люстр, подвешенных на цепях разной длины,
он использовал частоту биения своего пульса.
Маятники
используют для регулировки хода часов,
поскольку любой маятник имеет вполне
определённый период колебаний. Маятник
находит также важное применение в
геологической разведке. Известно, что
в разных местах земного шара значения
![]() – ускорение свободного падения, различны.
Различны они потому, что Земля – не
вполне правильный шар. Кроме того, в тех
местах, где залегают плотные породы,
например некоторые металлические руды,
значение
аномально высоко. Точные измерения
с помощью математического маятника
иногда позволяют обнаружить такие
месторождения.
– ускорение свободного падения, различны.
Различны они потому, что Земля – не
вполне правильный шар. Кроме того, в тех
местах, где залегают плотные породы,
например некоторые металлические руды,
значение
аномально высоко. Точные измерения
с помощью математического маятника
иногда позволяют обнаружить такие
месторождения.
Содержание
Предисловие |
3 |
|
§ 1 |
Основные понятия |
5 |
1.1. |
Координатная плоскость |
5 |
1.2. |
Углы и их измерение |
7 |
1.3 |
Тригонометрические функции угла |
9 |
1.4 |
Радианная система измерения углов (дуг) |
13 |
1.5 |
Аргумент тригонометрической функции |
18 |
§ 2 |
Основные теоремы тригонометрии |
22 |
2.1. |
Теорема синусов |
22 |
2.2 |
Теорема синусов |
25 |
2.3 |
Формулы приведения |
28 |
2.4 |
Прикладные аспекты основных теорем тригонометрии |
36 |
§ 3 |
Исследования тригонометрических функций числового аргумента |
47 |
3.1. |
Периодичность |
47 |
3.2. |
Тригонометрические функции , , , |
49 |
§ 4 |
Тригонометрические уравнения |
64 |
4.1. |
Простейшие тригонометрические уравнения |
64 |
4.2. |
Общий случай тригонометрических уравнений |
71 |
4.3. |
Понятие арксинуса, арксинуса, арктангенса и арктангенса числа для записи корней тригонометрических уравнений |
72 |
4.4. |
Тригонометрические уравнения, сводящиеся к простейшим |
76 |
§ 5. |
Приложение тригонометрических функций |
82 |
|
Библиографический список |
106 |
|
Приложение |
107 |
Библиографический список
Новоселов С.И. Специальный курс тригонометрии. –Изд. Высш. Ш., м.,1967. –535.
Никитин Ф.Ф. Математика: Учебник для десятых-одинадцатых классов среднеобразовательных учебных заведений. Часть 1.– Новосибирск: Изд. ИДМО,2000.–256 с.
Приложение
Таблица Брадиса тригонометрических функций

 ис.
5.2
ис.
5.2
 правка.
Каноническое уравнение окружности
радиусом
имеет вид
правка.
Каноническое уравнение окружности
радиусом
имеет вид
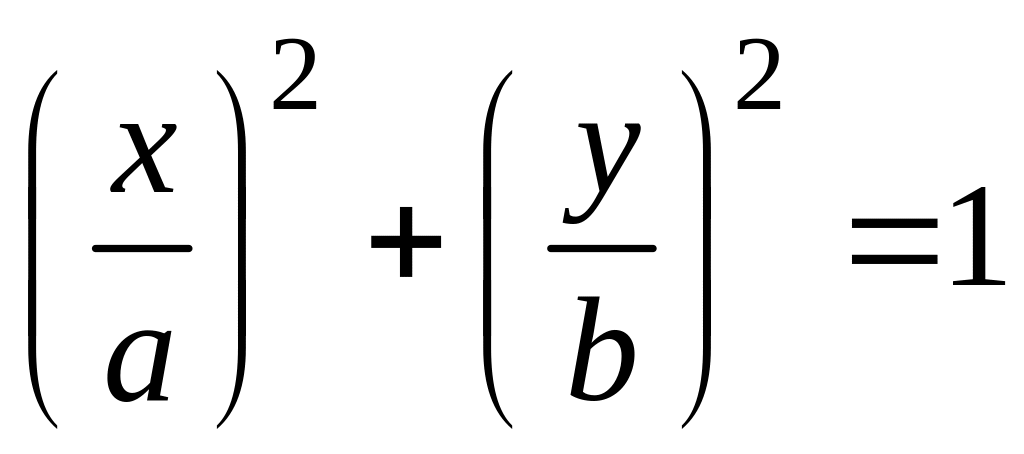 ,
,
 де
а – полуось эллипса на оси
,
– полуось эллипса на оси
.
де
а – полуось эллипса на оси
,
– полуось эллипса на оси
.