4.4. Тригонометрические уравнения, сводящиеся к простейшим

Тригонометрическими уравнениями называются уравнения, содержащие тригонометрические функции от неизвестной величины. Каждое значение, при подстановке которого вместо неизвестной величины получается верное равенство, называется решением или корнем тригонометрического уравнения.

Решить тригонометрическое уравнение значит найти все его корни или доказать, что уравнение корней не имеет.

Пример 4.1. Решить уравнение

. (а)

Решение. Заменим на и :

.

Подставим полученное выражение в уравнение (а) и преобразуем его, получим

.

Полученное уравнение сводится к решению двух уравнений:

Первое уравнение:

.

Второе уравнение, рис. 4.10:

И

Рис. 4.10

меем:

, тогда

.

Откуда .

Итак, уравнение (а) имеет два корня

Пример 4.2. Решить уравнение

. (б)

Решение. Заменим на :

.

Подставим полученное выражение в уравнение (б) и преобразуем его, получим

.

Полученное уравнение содержит только функцию . Введем обозначения: , тогда заданное уравнение сведется к квадратичному уравнению:

Таким образом, равенство возможно лишь тогда, когда или .

П

Рис. 4.11

ервое уравнение:

.

Второе уравнение (см. рис. 4.11):

Итак, уравнение (б) имеет три корня

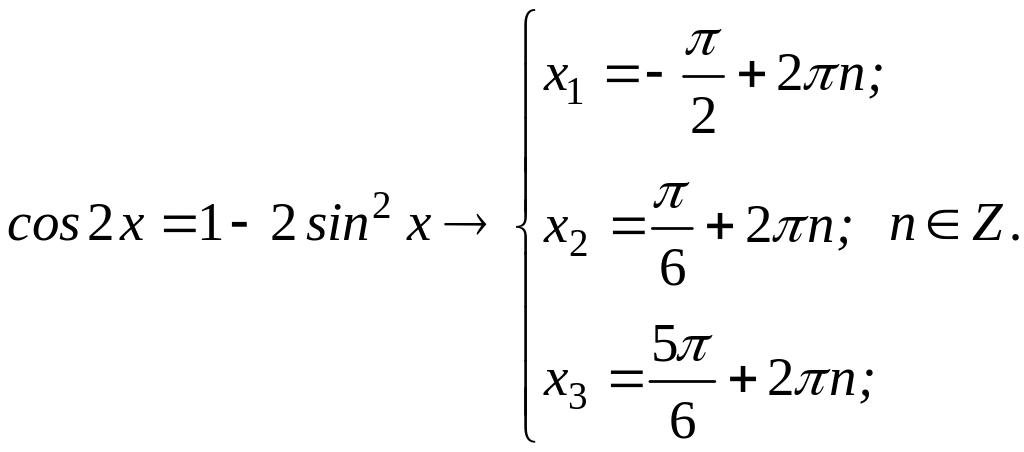
Пример 4.3. Решить уравнение

. (в)

Решение. Заменим на и :

.

Подставим полученное выражение в уравнение (в), получим

.

Отсюда

.

Разделим полученное уравнение на , получим

. (г)

Полученное уравнение содержит только функцию .

Пусть , тогда уравнение (г) будет иметь вид

Р

Рис. 4.12

ешим полученные простейшие тригонометрические уравнения (рис. 4.12).

1.

2.

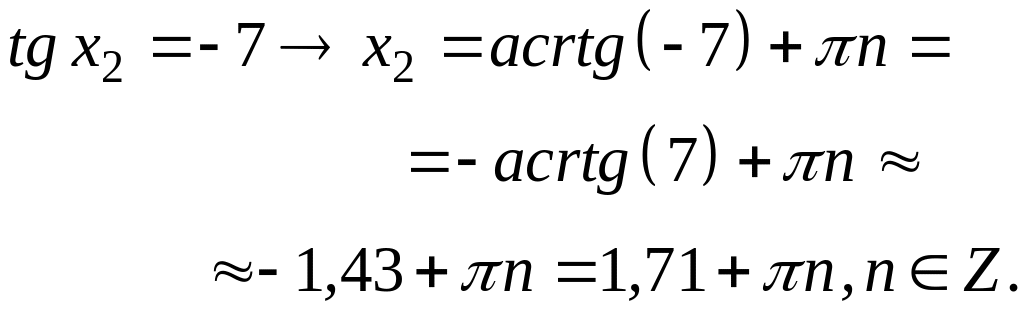
Справка: .

Пример 4.4. Решить уравнение:

.

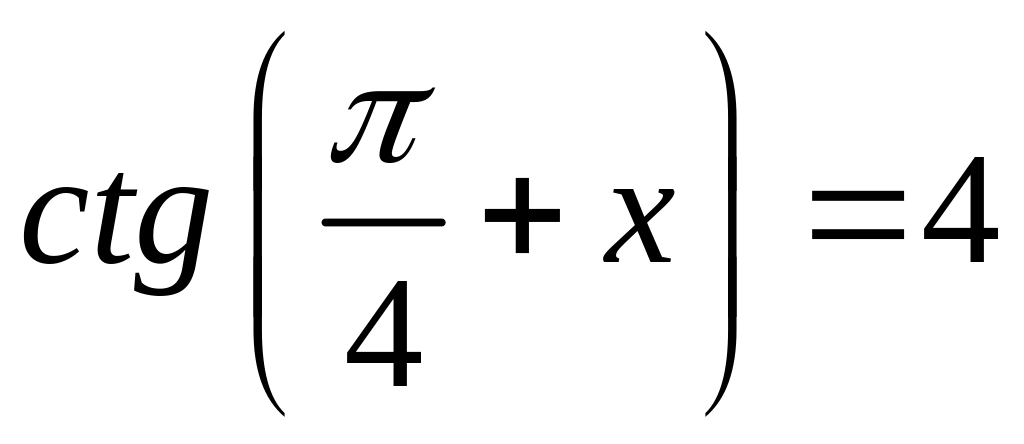Решение. Имеем

По общим формулам запишем ответ (числовые значения приведены в таблице 4.11):

Итак, получили

Таблица 4.11

x	sin x	cos x	tg x
0,25	0,2474	0,9689	0,2553
0,26	2571	9664	2660

Пример 4.5. Решить уравнение

. (а)

Решение. Пусть , тогда уравнение (а) будет иметь вид

Вычислим корни полученного уравнения

Уравнение (а) имеет единственное решение .

Имеем:

Пример 4.6. Решить уравнение

.

Решение. Пусть , тогда уравнение (а) будет иметь вид

, .

Разложим левую часть на множители, получим

,

откуда

Имеем

1.

2.

Пример 4.2. Решить уравнение

. (а)

Решение. Выразим косинус через синус

, тогда уравнение (а) примет вид

.

Введем обозначения: получим

Освободив уравнение от радикалов, получим

Имеем

Первое уравнение:

удовлетворяет уравнению (а) при , следовательно, для решения следует взять знак перед радикалом.

.

Замечание. Из общей формулы следует исключить нечетные значения, дающие для косинуса значение .

Второе уравнение:

.

Итак, заданное уравнение (а) имеет два корня