4.2. Общий случай тригонометрических уравнений

Рассмотрим уравнение вида

при различных значениях а. Для наглядности изобразим тригонометрические окружности, рис. 4.5.

Рис. 4.5

Точкам пересечения прямой « » с окружностью соответствуют все направленные углы, косинус которых равен а. В зависимости от значения а, возможны несколько случаев.

Случай 1. Пусть . Тогда прямая « » не пересекает тригонометрическую окружность, рис. 4.5, а, поэтому уравнение (4.5) не имеет решений. Например, уравнение не имеет решений, так как .

Случай 2. Пусть (рис. 4.5, б). Тогда прямая « » пересекает тригонометрическую окружность в единственной точке . Все направленные углы, которые соответствуют точке , можно записать в виде

, .

Случай 3. Пусть (рис. 4.5, в). Тогда прямая « » пересекает тригонометрическую окружность в единственной точке . Все направленные углы, которые соответствуют точке , можно записать в виде

, .

Случай 4. Пусть (рис. 4.5, д), например . Тогда прямая « » пересекает тригонометрическую окружность в двух точках и . Если известен один корень уравнения 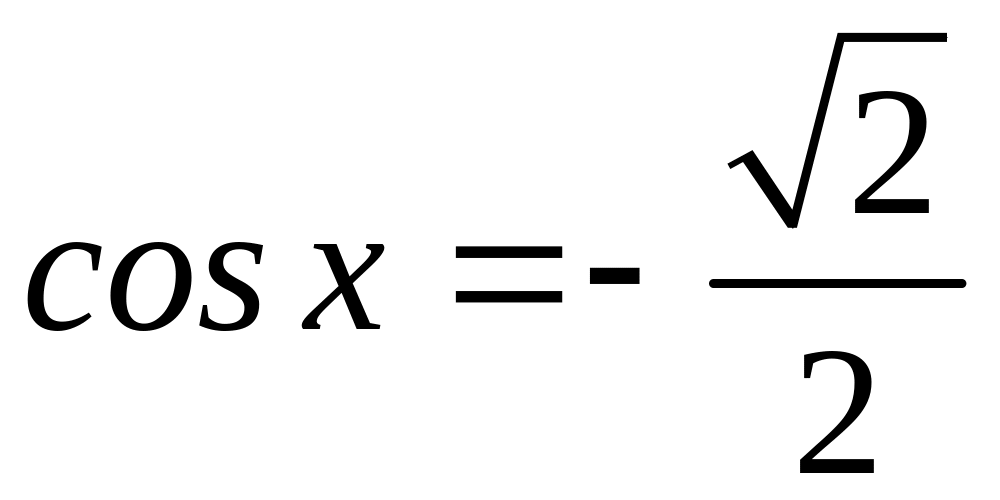( ), то все остальные корни можно найти точно так же, как это сделано в пункте II предыдущего параграфа, то есть

, .

4.3. Понятие арксинуса, арккосинуса, арктангенса и арктангенса числа для записи корней тригонометрических уравнений

I. Для записи одного из корней уравнения вводятся новое понятие и обозначение.

Определение При арксинусом числа а называется угол (в радианах) из промежутка , для которого . Арксинус числа записывается в виде .

Для изображения угла рассмотрим дугу тригонометрической окружности, рис. 4.6, а. Отметим на оси точку с ординатой и проведем через нее прямую « », перпендикулярную оси. Величина наименьшего по модулю направленного угла в радианах и есть . На рис. 4.6, б – угол , на рис 4.6, в – .

С использованием арксинуса при корни уравнения можно записать в виде двух видов чисел

Рис. 4.6

В таблице 4.5 приведены значения для некоторых значений .

Таблица 4.5

	1				0				-1
					0

Числовое значение для любого числа можно вычислить на калькуляторе или воспользоваться таблицей Брадиса, приведенной в приложении. Например, для уравнения по общим формулам можно сразу записать ответ (числовые значения приведены в таблице 4.6):

Таблица 4.6

x	sin x	cos x	tg x
0,66	0,6131	0,7900	0,7761
0,67	0,6210	0,7838	0,7923

II. Для записи одного из корней уравнения вводятся понятие и обозначение.

Определение При арккосинусом числа а называется угол (в радианах) из промежутка , для которого . Арккосинус числа записывается в виде .

Для изображения угла рассмотрим дугу тригонометрической окружности, рис. 4.7, а в промежутке . Отметим на оси точку с ординатой и проведем через нее прямую « », перпендикулярную оси . Величина наименьшего неотрицательного угла в радианах и есть (на рис. 4.6, б – угол ).

С

Рис. 4.7

использованием арккосинуса при общая форма корней уравнения может быть записана в виде:

В таблице 4.7 приведены значения для некоторых значений .

Числовое значение для любого числа можно вычислить на калькуляторе или воспользоваться таблицей Брадиса, приведенной в приложении.

Таблица 4.7

	1				0				–1
	0

Для уравнения по общим формулам можно сразу записать ответ (числовые значения приведены в таблице 4.8):

Таблица 4.8

x	sin x	cos x
0,85	0,7513	0,6600
0,86	7578	6524
0,87	7643	6448

III. Для записи одного из корней уравнения также вводятся понятие и обозначение.

Определение Для любого действительного числа арктангенсом числа называется величина в радианах такого угла из промежутка , что . Арктангенс числа записывается в виде .

Рис. 4.8

Корни уравнения при любом значении числа можно находить по формуле, рис. 4.8:

В таблице 4.9 приведены значения для некоторых значений .

Таблица 4.9

		-1		0		1
				0

К

Рис. 4.9

орни уравнения при любом значении числа можно находить по формуле, рис. 4.9:

Пример. Решить уравнение .

Решение. Для уравнения по общим формулам можно записать ответ (числовые значения приведены в таблице 4.9):

Таблица 4.10

x	sin x	cos x	tg x
0,55	0,5227	0,8525	0,6131
0,56	0,5312	0,8473	0,6269
0,57	0,5396	0,8419	0,6410

IV. Решение уравнения при сводится к решению уравнения вида ( ).

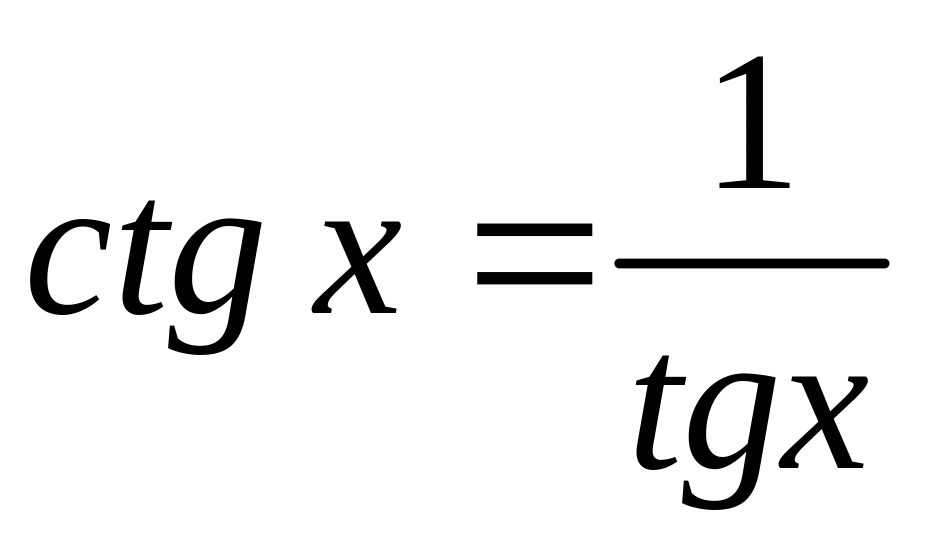Пример. Решить уравнение .

Решение. Данное уравнение равносильно уравнению

Имеем

В таблице 4.9 числовое значение .

Числовое значение для любого числа можно вычислить на калькуляторе или воспользоваться таблицей Брадиса, приведенной в приложении.