§ 4. Тригонометрические уравнения

4.1. Простейшие тригонометрические уравнения

I. Рассмотрим тригонометрическое уравнение

. (4.1)

По таблице тригонометрических функций 4.1 можно определить, что число является одним из корней уравнения (4.1).

Таблица 4.1

Радиан	0
	0						1

Для отыскания всех корней уравнения (4.1) изобразим тригонометрическую окружность и построим направленный угол величиной радиан, что соответствует , рис. 4.1. Затем построим график функции и проведем прямую , перпендикулярную оси синусов, которая пересекает ось в точке с ординатой .

Прямая « » содержит все точки координатной плоскости, ординаты которой равны . На рис. 4.1 нетрудно найти величины всех направленных углов, синус которых равен (красные точки). Один из направленных углов, соответствующий точке , был найден по таблице 4.1 и соответствует .

Р

Рис. 4.1

ис. 4.1

Все углы, которым соответствует точка , имеют вид

,

где – произвольное целое число.

Другой направленный угол, равный , соответствует точке .

Тогда величины углов, которым соответствует точка , имеют вид

,

где – произвольное целое число.

Таким образом, уравнение (4.1) имеет бесконечное число решений, которые можно записать в следующем виде:

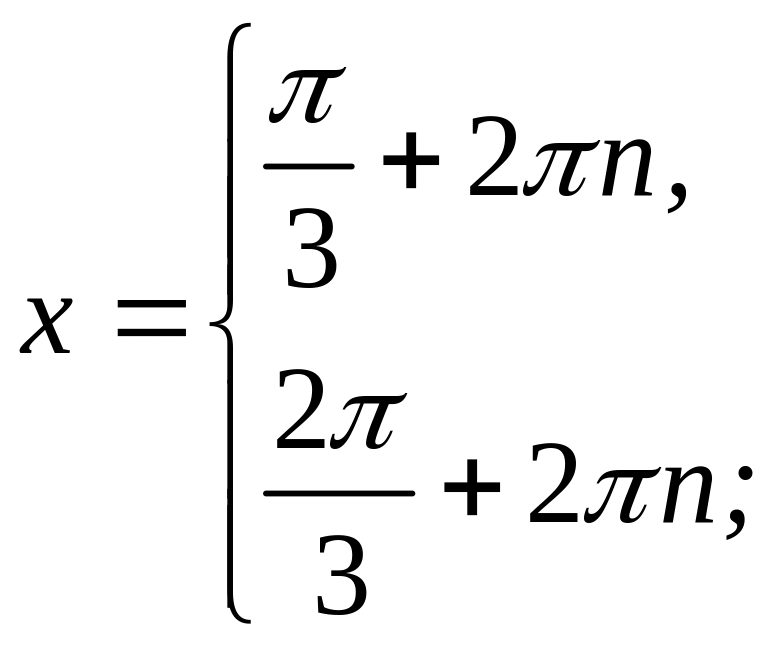где – произвольное целое число.

Аналогично решаются и другие уравнения.

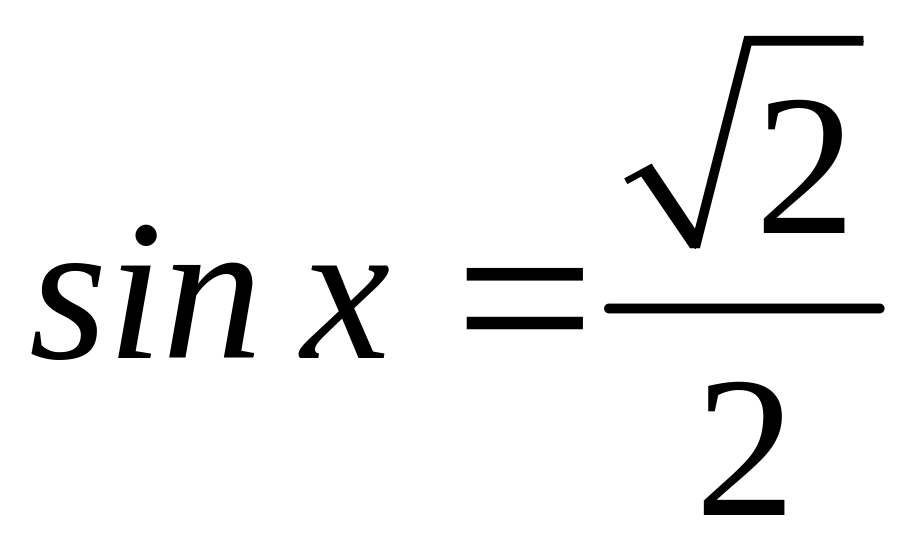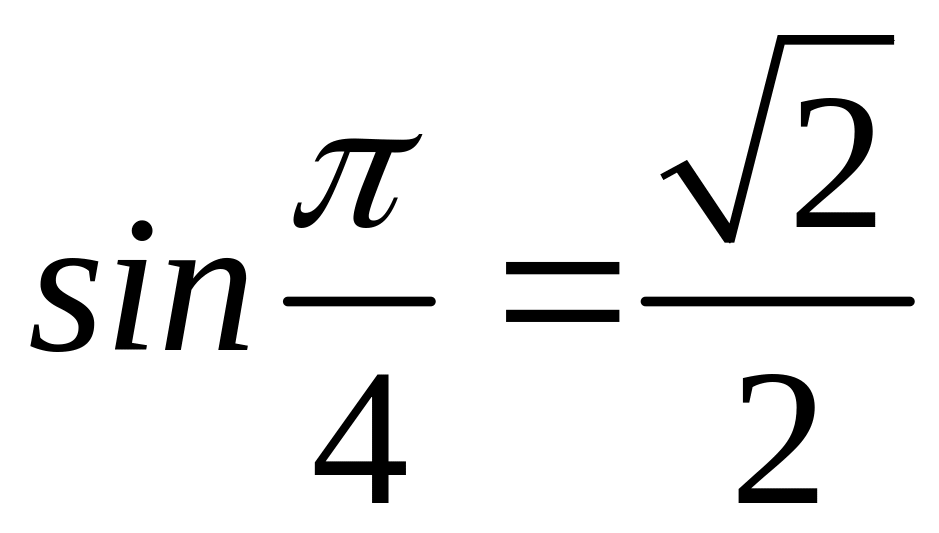Например, . Зная, что , можно записать

.

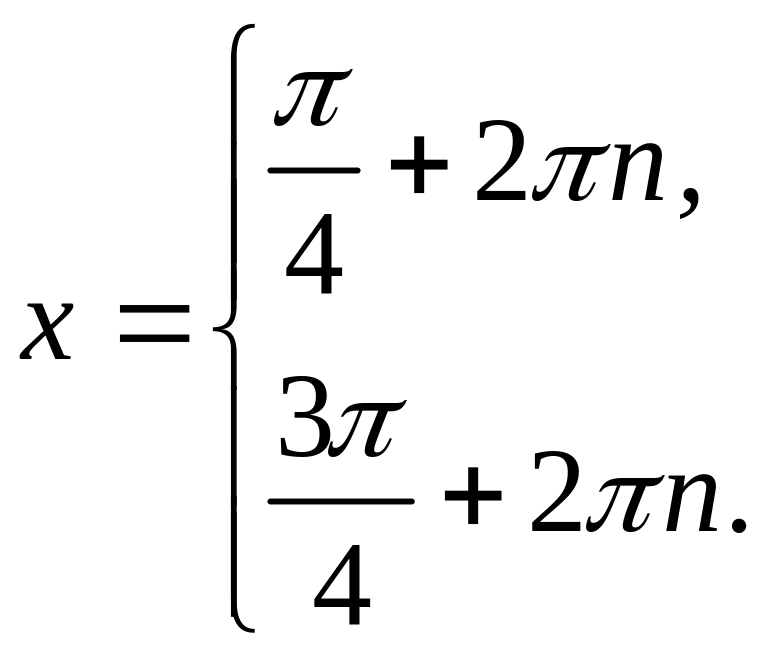
II. Рассмотрим тригонометрическое уравнение

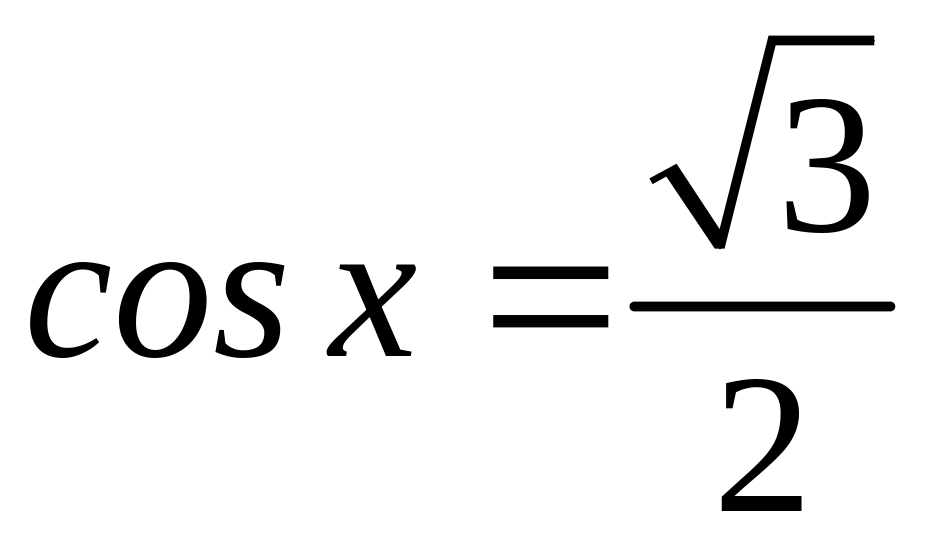. (4.2)

По таблице тригонометрических функций 4.2 можно определить, что число является одним из корней уравнения (4.2).

Таблица 4.2

Радиан	0
	1	0,96					0

Для отыскания всех корней уравнения (4.2) изобразим тригонометрическую окружность и построим направленный угол величиной радиан, что соответствует , рис. 4.2. Затем построим график функции и проведем прямую , перпендикулярную оси , которая пересекает ось в точке с ординатой . Прямая « » содержит все точки координатной плоскости, ординаты которой равны . На рис. 4.2 нетрудно найти величины всех направленных углов, косинус которых равен (красные точки).

Один из направленных углов, соответствующий точке , был найден по таблице 4.2: .

В

Рис. 4.2

се углы, которым соответствует точка , имеют вид:

,

где – произвольное целое число.

Другой из направленных углов, равный , соответствует точке .

Тогда величины углов, которым соответствует точка , имеют вид

,

где – произвольное целое число.

Таким образом, уравнение (4.2) имеет бесконечное число решений, которые можно записать в следующем виде

где – произвольное целое число.

Аналогично решаются и другие уравнения. Например, .

Зная, что , можно записать решение в виде , .

III. Рассмотрим тригонометрическое уравнение

. (4.3)

По таблице тригонометрических функций 4.3 можно определить, что число является одним из корней уравнения (4.3).

Таблица 4.3

радиан	0
	0			1

Для получения всех корней этого уравнения изобразим тригонометрическую окружность и построим график функции , далее проведем прямую , перпендикулярную оси , которая пересекает эту ось в точке с ординатой , рис. 4.3.

Рис. 4.3

Прямая « » содержит все точки координатной плоскости, ординаты которой равны . На рис. 4.3 нетрудно найти величины всех направленных углов, тангенс которых равен (красные точки).

Один из направленных углов, соответствующий точке , был найден по таблице 4.3: . Все углы, которым соответствует точка , имеют вид: , где – произвольное целое число.

Другой направленный угол, соответствующий точке , равен . Все углы, которым соответствует точка , имеют величины .

Таким образом, уравнение (4.3) имеет бесконечное число решений, которые в общем виде можно записать в следующем виде

, .

IV. Рассмотрим тригонометрическое уравнение

. (4.4)

По таблице тригонометрических функций 4.4 можно определить, что число является одним из корней уравнения (4.4).

Таблица 4.4

радиан	0
	0			1

Для получения всех корней этого уравнения изобразим тригонометрическую окружность и построим график функции , далее проведем прямую , перпендикулярную оси , которая пересекает эту ось в точке с ординатой 1, рис. 4.4.

П

Рис. 4.4

рямая « » содержит все точки координатной плоскости, ординаты которой равны 1. На рис. 4.3 нетрудно найти величины всех направленных углов, тангенс которых равен 1 (красные точки). Один из направленных углов, соответствующий точке , был найден по таблице 4.4 – . Все углы, которым соответствует точка , имеют вид:

,

где – произвольное целое число.

Другой направленный угол, соответствующий точке , равен . Все углы, которым соответствует точка , имеют величины .

Таким образом, уравнение (4.4) имеет бесконечное число решений, которые в общем виде можно записать в следующем виде

, .