§ 3. 2. Тригонометрические функции , , ,

Градусное измерение углов удобно на практике тем, что в нем единица измерения (градус – ) соизмерима с полным оборотом, введение радиальной меры ( ) целесообразно при изучении тригонометрических функций.

Синусом числа называется синус направленного угла, соответствующего радианам. Таким образом, по определению

.

На рис. 3.4 показано значение функции при . Значение равно ординате точки на единичной окружности, определяющей дугу длины 1 радиан, которая соответствует направленному углу , т. е. .

П

Рис. 3.4

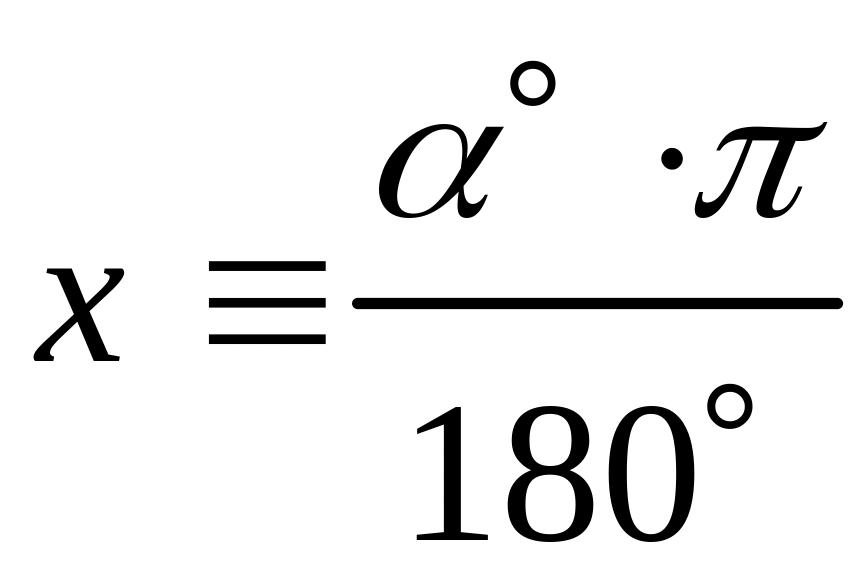ри переходе от градусной меры в радианную ( ) в тригонометрических функциях угла определяются тригонометрические функции аргумента x – :

; ;

; .

В

Рис. 3.5

ыберем окружность единичного радиуса (рис. 3.5). Под произвольным углом от начального радиуса проведем луч из центра окружности. Этот луч пересечет дугу окружности единичного радиуса в точке . Пусть и – координаты точки на оси . Как было показано, отношение катетов к гипотенузе в зависят лишь от направления луча, определяемого углом .

Тогда, если , то отношения и :

_{, .}

Ось в тригонометрии принято называть осью косинусов, а ось – осью синусов (рис. 3.4).

Используя теорему Пифагора, запишем связь между тригонометрическими функциями и _.

_Имеем:

_{. (1)}

_В

Рис. 3.6

ыражение (1) называется _{основным тригонометрическим тождеством.}

Четность и нечетность тригонометрических функций. Рассмотрим точки и на единичной окружности, изображающие взаимно противоположные значения аргумента и , симметричные относительно оси (рис. 3.6).

Следовательно, точки и имеют одну и ту же координату и взаимно противоположные координаты и .

Имеем:

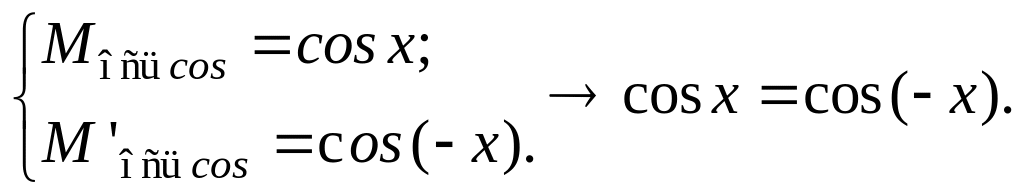
Следовательно, функция косинуса – четная функция: , а функция синуса – функция нечетная: .

График функции . Выберем произвольное число . Сопоставим этому числу направленный угол, радианная мера которого равняется радианам.

Построим график функции на отрезке . Пусть центр единичной окружности лежит на пересечении осей и . Разделим отрезок на оси на 6 равных частей (рис. 3.7). Ординаты точек на окружности – это синусы соответствующих углов: , , , , , . Отложим эти ординаты в радианах от соответствующих точек отрезка . Перевод градусов в радианы приведен в таблице 3.1.

_{Таблица 3.1}

Градусы ( )
Радиан ( )

Соединяя полученные точки плавной кривой, получим часть графика функции на отрезке

Рис. 3.7

Как видно из графика, в первой четверти синус возрастает от 0 до 1.

В таблице 3.2 приведены значения синуса на отрезке

Таблица 3.2

,градус	0
,радиан	0
	0	0.26	0,5			0,96	1
	0	0.26	0,52	0,78	1,05	1,31	1,57

Эти значения тригонометрических функций для называют значениями тригонометрических функций в смысле главного значения!

Отметим, что линейная функция совпадает с функцией на отрезке ! (рис. 3.7).

Построим график функции на отрезке . Разделим второй квадрант окружности и отрезок на 6 равных частей (рис. 3.8). Ординаты точек на окружности – это синусы соответствующих углов: , , , , , .

Таблица 3.3

Градусы	90o						180о
Радианы		1,83		2,35	2,62	2,88	3,14

Отложим эти ординаты в радианах от соответствующих точек отрезка . Перевод градусов в радианы приведен в таблице 3.3. Соединяя полученные точки плавной кривой, получим часть графика функции на отрезке (рис. 3.8).

Рис. 3.8

Как видно из графика, во второй четверти синус убывает от 1 до 0. В точках (например, ) и (например, ), расположенных на единичной окружности симметрично относительно оси ординат (оси ), значение синусов равны!

.

Числовые значения синуса в этой четверти представлены в таблице 3.4.

Таблица 3.4

, градус
, радиан
	1	0,96			0,5	0.26	0
Справка. Введем понятие осевой симметрии. Осевой симметрией в математике называется зеркальное отражение относительно некоторой линии (прямой ) на плоскости. Она предполагает, что если через каждую точку оси симметрии провести перпендикуляр, то на нем всегда можно найти 2 симметричные точки, расположенные на одинаковом расстоянии от оси, т. е. выполняется равенство . Прямая, относительно которой существуют симметричные точки, является осью симметрии графика функции.

График синуса во второй четверти симметричен графику в первой четверти относительно параллели оси ординат, проходящей через точку (рис. 3.9).

Рис. 3.9

Аналогично построим график функции на отрезке (рис. 3.10).

Рис. 3.10

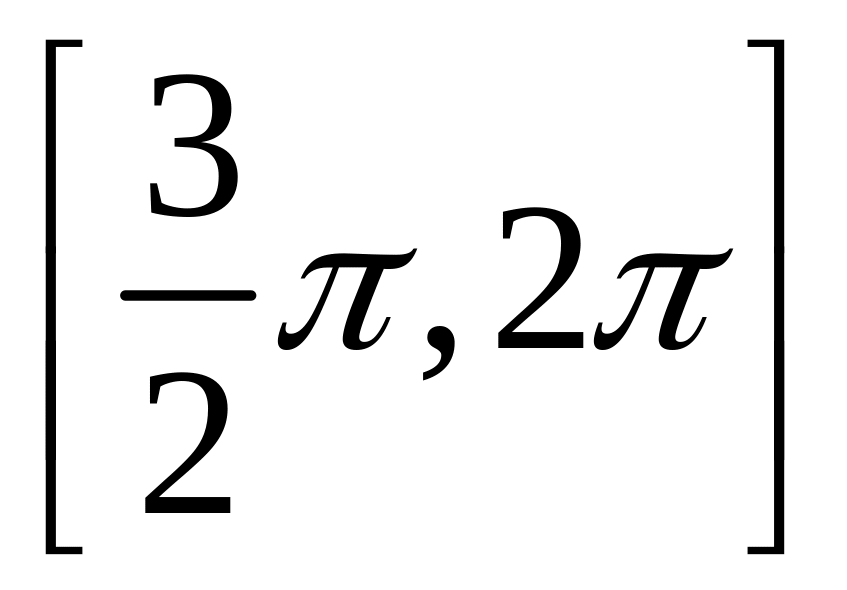Как видно из графика (рис. 3.10), в третьей четверти синус убывает от 0 до –1, а в четвертой возрастает от –1 до 0. График синуса на отрезке симметричен графику синуса на отрезке относительно параллели оси ординат, проходящей через точку (рис. 3.11).

Рис. 3. 11

Передвигая полученную часть влево и вправо вдоль оси на расстояния мы сможем построить весь график функции (рис. 3.12).

Рис. 3. 12

Отметим свойства графика функции :

1. Синусоида симметрична относительно начала координат:

.

2. При 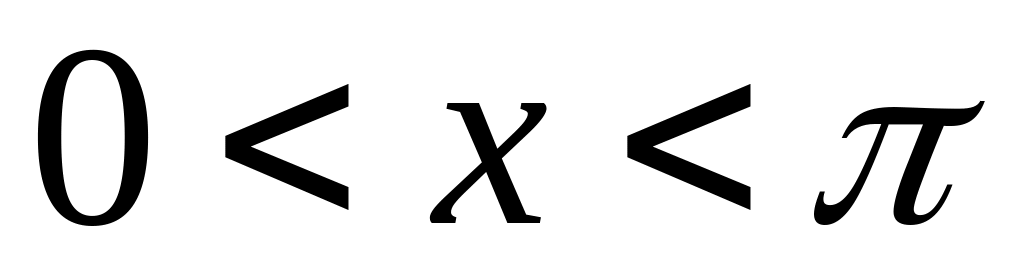в точках и значения синуса равны

.

Функция является примером периодической функции с периодом, равным . График функции называется синусоидой.

График функция . Косинус действительного числа определяется аналогично тому, как был определен синус (рис. 3.13).

К

Рис. 3.13

осинусом числа называется косинус направленного угла, соответствующего радианам. Таким образом, по определению

.

Как видно из графика, в первой и второй четвертях на отрезке косинус убывает от +1 до –1. В третьей и четвертой четвертях на отрезке косинус возрастает от 0 до 1.

График функции на отрезке симметричен графику косинуса на отрезке относительно параллели оси ординат, проходящей через точку (рис. 3.13).

Развернем график функции косинуса, построенного на рис. 3.13, на , получим график функции косинуса в традиционной ориентации декартовых осей (рис. 3.14).

Рис. 3.14

Отметим свойства графика функции :

1. Косинусоида симметрична относительно оси :

.

2. При в точках и значения косинуса равны:

.

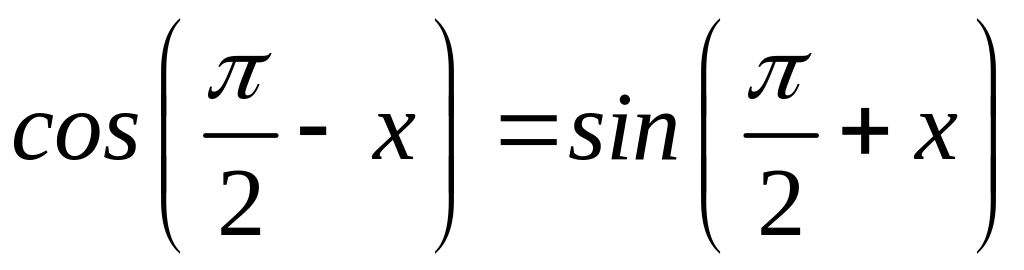График функции можно получить смещением влево в направлении оси абсцисс на расстояние графика функции , поскольку , рис. 3.15. Следовательно, разница между и состоит только в сдвиге фаз на .

Рис. 3.15

Функция является примером периодической функции с периодом, равным . График функции называется косинусоидой. Числовые значения косинуса на отрезке представлены в таблице 3.5.

Таблица 3.5

,градус	0
,радиан	0
	0	0.96			0,5	0.26	1

Мы получили, что функции и периодические, их наименьший положительный период равен (см. рис. 3.12 и 3.14).

Ф Рис. 3.16 ункция . Придадим тангенсу геометрический смысл. Определим ось тангенсов. Функции синуса и косинуса определены как ордината и абсцисса точки (рис. 3.16), а тангенс – алгебраически как . Определим ось тангенса. Для этого проведем через точку с координатами (начало отсчета на тригонометрической окружности) касательную к тригонометрической окружности – прямую, параллельную оси ординат. Назовем эту прямую осью тангенсов (рис. 3.16). Название это оправдывается так: пусть – точка на тригонометрической окружности, соответствующая числу ( ).Продолжим радиус до пересечения с осью тангенсов. Тогда оказывается, что ордината точки пересечения .

Докажем это утверждение. Треугольники и , очевидно, подобны. Отсюда

.

Если точка имеет координаты или , то прямая параллельна оси тангенсов, и тангенс геометрически определить нельзя.

График функция . Построение графика функции можно с какой угодно степенью точности выполнить геометрически. Достаточно разделить первую четверть тригонометрического круга и промежуток на числовой оси на одинаковое количество равных частей и перенести линии тангенса в качестве ординат, восстановленных в соответствующих точках (рис. 3.17).

Тангенсоида – так называется график функции . На отрезке тангенс возрастает от 0 до , следовательно, график имеет вертикальную асимптоту.

Числовые значения косинуса на отрезке представлены в таблице 3.6. Таблица 3.6

, градус	0
, радиан	0
	0			1
	0	0.26	0,52	0,78	1,05		1,31	1,57
Рис. 3. 17						Справка. Асимптоты – прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом различаются два вида асимптот: вертикальные и наклонные.

График функции на всей числовой оси имеет такой вид, как на рис. 3.18. Функция является еще одним примером периодической функции.

Рис. 3. 18

График функции на всей числовой оси имеет такой вид, как на рис. 3.19.

Рис. 3. 19

Числовые значения косинуса на отрезке представлены в таблице 3.7.

Таблица 3.7

(градус)	0
(радиан)	0
				1			0

Историческая справка. Название «тангенс», происходящее от латинского “tanger” (касаться), появилось в 1583 г. Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности). Тангенсы возникли в связи с решением задачи о вычислении длины тени. Тангенс (а также котангенс) ввел в 10 в. аль-Батани (850-929) и абу-эль-Вефа Мухамед-бен Мухаммед (940-998), который составил таблицы синусов и тангенсов через с точностью до 1/604. На окружности единичного радиуса вводятся оси косинусов, синусов, тангенсов и котангенсов (рис. 3.20).

В 8 в. н.э. ученые стран Ближнего и Среднего Востока познакомились с трудами индийских математиков и астрономов и перевели их на арабский язык. В середине 9 в. среднеазиатский ученый аль-Хорезми написал сочинение «Об индийском счете». После того как арабские трактаты были переведены на латынь, многие идеи индийских математиков стали достоянием европейской, а затем и мировой науки. Постепенно тригонометрия органически вошла в математический анализ, механику, физику и технические дисциплины.

Рис. 3. 20

Н. Коперник добавил таблицу секансов, что позволило ему заменять деление (на синус и косинус) умножением в целях облегчения вычисления. Знаменитый астроном Тихо-Браге (1546-1601) разработал много вычислительных приемов, облегчающих задачу решения треугольников, как плоских, так и сферических. Таблицы тригонометрических функций, по форме и составу близкие к современным, составил в 1551 г. Ретик, ученик Коперника. К концу 16 в. устойчивый характер приобрели названия всех тригонометрических функций. Ф. Виет дополнил и систематизировал различные случаи решения плоских и сферических треугольников, открыл формулы для тригонометрических функций от кратных углов. В 1770 г. появилась книга Г.С. Клюгеля «Аналитическая тригонометрия», где даны определения тригонометрических функций, которые существуют и в наши дни.