6.5. Похідні основних елементарних функцій

1. Похідна логарифмічної функції. Якщо , то

.

Доведення. Нехай х довільна точка із (0; ∞). Візьмемо приріст аргументу і знайдемо приріст функції

.

Отже,

.

Звідси, за допомогою граничного переходу, використовуючи другу важливу границю, одержимо

, де , . Отже, .

Наслідок. При , маємо: .

2. Похідна показникової функції. Функція є оберненою до функції . Тоді, згідно з правилом диференціювання оберненої функції, знаходимо . Оскільки , то одержимо формулу . Зокрема, для , маємо .

3. Похідна степеневої функції. Функція при x>0 може бути представлена у вигляді . Використовуючи правила диференціювання показникової та складної функцій, одержимо

.

Якщо x<0, то функцію можна подати інакше: . Тоді .

Нехай . Вираз визначений тільки тоді, коли . У цьому випадку

.

Таким чином, приходимо до висновку: похідна степеневої функції може бути знайдена за формулою для будь-яких α і x, для яких має зміст права частина цієї формули.

Приклад. Знайти похідну функції . Використавши формулу для похідної степеневої функції, дістанемо:

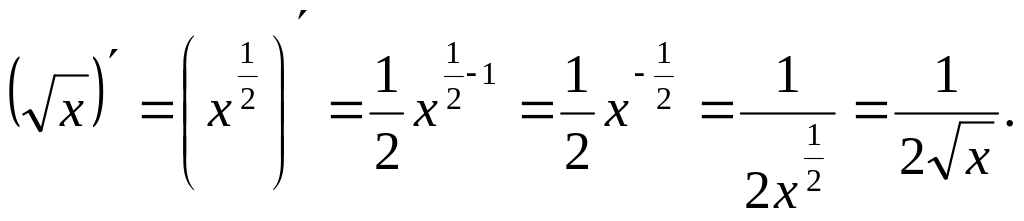
4. Похідні тригонометричних функцій. Для знаходження похідної від функції скористаємося формулою , першою чудовою границею і неперервністю функції :

Скориставшись тригонометричною тотожністю і правилом диференціювання складної функції, одержимо

Для знаходження похідної функції використаємо формулу похідної частки двох функцій

.

Аналогічно

5. Похідні обернених тригонометричних функцій. Функція є оберненою для функції . Скориставшись формулою похідної від оберненої функції, одержимо: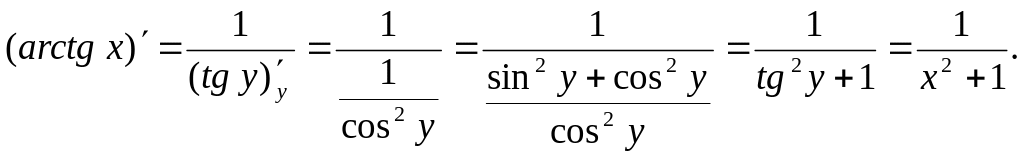

Аналогічно функція є оберненою для функції . Отже,

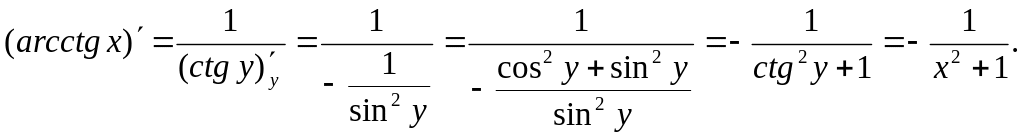
Функція є оберненою для функції . Отже,

Аналогічно функція є оберненою для функції . Отже,

6. Диференціювання функцій, заданих неявно. Якщо функціональну залежність між у та х задано неявно, тобто рівністю , тоді для знаходження похідної функції у по х треба продиференціювати тотожність , враховуючи, що у залежить від х, а потім розв’язати рівняння, яке одержали, відносно : , .

Приклад. Знайти похідну функції у, яка задана рівнянням і обчислити її значення в точці (2; 1).

Розв’язування. Диференціюючи обидві частини рівняння і враховуючи, що у залежить від х, одержимо , звідки .

Значення похідної при буде дорівнювати .

7. Диференціювання функцій, заданих параметрично.

Нехай залежність у від х задана параметрично у вигляді , де t – параметр. Якщо t одержить приріст , то х та у також одержать прирости, відповідно: , , причому при та . Тому . Таким чином похідна функції, яка задана параметрично, знаходять за формулою .

Основні правила та формули для знаходження похідних подаємо у вигляді таблиці.

Таблиця правил та формули обчислення похідних

№ п/п	Функція у	Похідна	№ п/п	Функція у	Похідна	№ п/п	Функція у	Похідна
1	с	0	9			17
2	x	1	10			18
3	cu		11			19
4	u ± v		12			20
5	u∙v		13			21
6			14			22
7			15			23
8			16			24