Классификация нелинейных функций.

различают два класса нелинейных регрессий:

1. регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. Примером этого класса моделей могут служить полиномы разных степеней у = а + вх + сх²; у = а + вх + сх²+ dх³, а также равносторонняя гипербола

у = в + а/х.

2. нелинейные регрессии по оцениваемым параметрам:

• степенная у = а х^в

• показательная у = а в^х

• экспоненциальная у = е ^{а+ вх}.

Первый класс моделей (нелинейных по переменным) не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в параболе у = а + вх + сх² , заменяя переменные х₁=х, а х₂=х² , получаем двухфакторное уравнение линейной регрессии у = а + вх₁ + сх₂. Соответственно для полинома третьего порядка получим трехфакторную модель линейной регрессии и так далее. Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров. Среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени, в отдельных случаях – полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и, соответственно, тем менее однородна совокупность по результативному признаку.

Для равносторонней гиперболы мы можем заменить 1/х на z и получим линейное уравнение регрессии, оценка параметров которого может быть дана МНК.

Иначе обстоит дело со вторым классом моделей, то есть с регрессией, нелинейной по оцениваемым параметрам. Данный класс нелинейных моделей можно разделить на два типа: а) нелинейные модели внутренне линейные и б) нелинейные модели внутренне нелинейные.

Если модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Пример – степенная функция у = а х^в. Данная модель нелинейна относительно оцениваемых параметров, так как включает параметры а и в неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения приводит его к линейному виду. Соответственно оценки параметров а и в могут быть найдены МНК.

Внутренне нелинейной будет модель вида у = а + вх^с, так как ее невозможно превратить в линейный вид никакими преобразованиями переменных.

Как и в парной зависимости, возможны разные виды уравнений множественной регрессии: линейные и нелинейные. Ввиду четкой интерпретации параметров уравнения наиболее широко используются линейные и степенные функции. Линейная модель в форме является аддитивной. Это означает, что в основе модели лежит гипотеза о том, что каждый фактор что-то добавляет или отнимает от значения результативного признака. Например, если у – это урожайность сельскохозяйственной культуры, а х₁, х₂ и х₃ – агротехнические факторы: дозы удобрений, число прополок, поливов и т.п., то каждый из этих факторов либо повышает, либо понижает величину урожайности, причем последняя могла бы существовать и без этих факторов.

Однако аддитивная модель пригодна не для любых связей в экономике. Если, например, изучается зависимость объема продукции предприятия от занимаемых площадей, числа работников, стоимости основных фондов (или всего капитала), то каждый из факторов является необходимым для существования результата, а не добавлением к нему. В таких ситуациях нужно исходить из гипотезы о мультипликативной форме модели:

Такая модель по ее первым создателям получила название модель Кобба-Дугласа. Это степенная функция и, как мы уже знаем, показатели степени при факторах являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1 процент при неизменности других факторов. Решение степенной функции методом наименьших квадратов требует предварительной ее линеаризации. Как было рассмотрено ранее (лекция 4), линеаризация степенных функций проводится с помощью логарифмирования ее переменных.

Степенные множественные функции часто используются как производственные функции, где результатом выступают объемы производства, а факторами – используемые ресурсы (трудовые ресурсы, основные производственные фонды, машины, текущие затраты и т.п.). Экономический смысл здесь имеют не только коэффициенты эластичности по каждому фактору, но и их сумма

B = b₁+b₂

Эта величина фиксирует обобщенную характеристику эластичности производства (показывает, на сколько процентов в среднем увеличиваются объемы производства при увеличении всех факторов на 1%).

Возможны и другие линеаризуемые функции для построения уравнения множественной регрессии. Например,

экспонента

или гипербола

Стандартные компьютерные программы обработки регрессионного анализа позволяют перебирать различные функции и выбирать ту из них, для которой остаточная дисперсия и ошибка аппроксимации минимальные. Однако следует помнить, что чем сложнее сама функция, тем менее интерпретируемы ее параметры. При сложных полиномиальных функциях необходимо соблюдать соотношение между числом объясняющих переменных и объемом совокупности. Так, полином второй степени с двумя факторами

y = a + b₁x₁ + b₂x₂ +b₁₁x₁²+ b₂₂ x₂ ²+ b₁₂x₁x₂

требует не менее 40-50 наблюдений.

Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем тесноты связи, а именно – индексом корреляции R

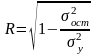(4.18)

где -общая дисперсия результативного признака;

- остаточная дисперсия.

Учитывая связь дисперсии с объемом вариации, можно легко доказать, что индекс корреляции через объемы вариации определяется следующим образом:

Индекс детерминации используется для проверки существенности уравнения нелинейной регрессии в целом по F-критерию Фишера

F = 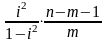(4.20)

где п – число наблюдений;

т – число параметров при переменных х.

9. Эконометрическое моделирование одномерных и многомерных временных рядов

Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов (периодов) времени. Реальные данные временного ряда могут складываться при одновременном влиянии трех перечисленных компонент, факторы уровней временного ряда по характеру воздействия можно условно разбить на три группы:

1. факторы, формирующие тенденцию ряда (Т);

2. факторы, формирующие циклические колебания ряда (S);

3. случайные факторы (E).

В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма компонент, называется аддитивной. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной. Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент, с тем чтобы использовать полученную информацию для прогнозирования будущих значений ряда.

Процесс построения модели включает в себя следующие шаги:

1. Выравнивание исходного ряда методом скользящей средней

2. Расчет значений сезонной компоненты

3. Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных (Т+Е) в аддитивной модели или (Т*Е) в мультипликативной модели.

4. Аналитическое выравнивание уровней (Т+Е) или (Т*Е) и расчет значений Т с использованием поученного уравнения тренда.

5. Расчет полученных по модели значений (Т+S) или (Т*S)

6. Расчет абсолютных и/или относительных ошибок. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок E для анализа взаимосвязи ряда и других временных рядов.

Выбор между аддитивной моделью и мультипликативной осуществляется на основе анализа изменения амплитуды колебаний (если в динамике амплитуда колебаний увеличивается или уменьшается, то мультипликативная модель).

Прогнозное значение уровня временного ряда в аддитивной модели - это сумма трендовой и сезонной компонент (по тренду, подставив в уравнение t_n , определяем значение T и складываем с соответствующим этому t_n значением сезонной компоненты S).

Прогнозное значение временного ряда в мультипликативной модели – это произведение трендовой и сезонной компонент. Для определения T используем уравнение тренда и умножаем на соответствующее прогнозируемому периоду значение сезонной компоненты S.

Изучение взаимосвязи экономических переменных по данным временных рядов осложнено тем, что в этих рядах может быть тенденция. Если в ряду динамики переменной у и в ряду динамики х есть компонента «Т», то в результате мы получим тесную связь между у и х. Однако из этого факта еще нельзя делать вывод о том, что изменение х есть причина изменения у, то есть что между этими изменениями есть причинно-следственная связь.

Чтобы выявить причинно-следственную зависимость между переменными, необходимо устранить ложную корреляцию между ними, вызванную наличием тенденции.

Существует несколько способов исключения тенденции в рядах динамики. Первый способ называется метод отклонений от тренда. Пусть имеется у_t= Т + е и х_t= Т + е. Проводится аналитическое выравнивание каждого ряда: и , где Т_у и Т_х – это оценки трендовых компонент. Затем определяется остаток в каждом наблюдении и

, так как остаточная компонента не содержит тенденции. Далее изучается зависимость между самими остатками е_у=f(е_х). Если между переменными есть связь, то она проявится в согласованном изменении остатков. Недостатком данного способа является то, что содержательная интерпретация параметров такой модели затруднительна. Однако модель может быть использована для прогнозов и, кроме того, коэффициент парной корреляции между остатками отразит связь переменных.

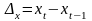Второй способ преодоления тенденции в рядах динамики – это метод последовательных разностей. Если временной ряд содержит ярко выраженную линейную тенденцию, то для ее устранения можно заменить исходные уровни разностями первого порядка, то есть цепными абсолютными приростами: и . Далее прирост у рассматривается как функция прироста х: .

Третьим способом является включение в модель регрессии фактора времени: y_t= a+b₁x₁+ b₂ t. В данном случае коэффициенты чистой регрессии легко интерпретируются, имеют естественные единицы измерения. Коэффициент b₁ покажет на сколько единиц изменится результат при единичном изменении фактора при условии существования неизменной тенденции; коэффициент b₂ отразит влияние всех прочих факторов, формирующих тенденцию, кроме x₁. Однако данный способ построения регрессионной модели требует большего объема наблюдений, так как в модели появляется еще один параметр.