1. Классическая линейная модель множественной регрессии в матричной форме. Метод наименьших квадратов

Идея множественной регрессии состоит в том, что зависимая переменная определяется более чем одной объясняющей переменной. Общий вид множественной регрессии:

Коэффициенты регрессии показывают, насколько изменится значение зависимой переменной y, если значение соответствующей независимой переменной изменится на 1, при условии, что все остальные переменные останутся неизменными.

Матричная форма записи

Пусть имеется выборка из n наблюдений, а модель включает k независимых переменных и константу. Введем обозначения:

Y= - вектор-столбец наблюдений (размерности n)

X= — матрица значений независимых переменных (размерности n на k+1)

- вектор-столбец неизвестных параметров, (размерности k+1)

- вектор-столбец случайных ошибок,(размерности n)

Тогда множественную линейную регрессионную модель можно записать, в матричной форме:

В результате оценивания модели множественной регрессии определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Суть метода наименьших квадратов состоит в том, чтобы найти такой вектор β оценок неизвестных коэффициентов модели, при которых сумма квадратов отклонений (остатков) наблюдаемых значений зависимой переменной у от расчётных значений ỹ (рассчитанных на основании построенной модели регрессии) была бы минимальной.

Матричная форма функционала F метода наименьших квадратов:

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β0…βk, потому что значения результативной и факторных переменных известны из наблюдений. Для определения минимума функции (1) необходимо вычислить частные производные этой функции по каждому из оцениваемых параметров и приравнять их к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (1):

Общий вид стационарной системы уравнений для функции (1): Решением стационарной системы уравнений будут МНК-оценки неизвестных параметров линейной модели множественной регрессии:

2. Предпосылки построения множественной регрессии и их запись в матричной форме

Условия построения нормальной линейной модели множественной регрессии, записанные в матричной форме:

1) факторные переменные x_1k…x_nk – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии ε_n. В терминах матричной записи Х называется детерминированной матрицей ранга (k+1), т.е. столбцы матрицы X линейно независимы между собой и ранг матрицы Х равен m+1<n;

2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

3) предположения о том, что дисперсия случайной ошибки модели регрессии является постоянной для всех наблюдений и ковариация случайных ошибок любых двух разных наблюдений равна нулю, записываются с помощью ковариационной матрицы случайных ошибок нормальной линейной модели множественной регрессии:

где

G2 – дисперсия случайной ошибки модели регрессии ε;

In – единичная матрица размерности (n*n).

4) случайная ошибка модели регрессии ε является независимой и независящей от матрицы Х случайной величиной, подчиняющейся многомерному нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2

В нормальную линейную модель множественной регрессии должны входить факторные переменные, удовлетворяющие следующим условиям:

1) данные переменные должны быть количественно измеримыми;

2) каждая факторная переменная должна достаточно тесно коррелировать с результативной переменной;

3) факторные переменные не должны сильно коррелировать друг с другом или находиться в строгой функциональной зависимости.

3. Свойства оценок выборочных коэффициентов регрессии, полученных методом наименьших квадратов. Теорема Гаусса-Маркова

Оценки по обычному методу наименьших квадратов являются не только несмещенными оценками коэффициентов регрессии, но и наиболее эффективными в том случае, если выполнены условия Гаусса—Маркова. С другой стороны, если условия Гаусса—Маркова не выполнены, то, вообще говоря, можно найти оценки, которые будут более эффективными по сравнению с оценками, полученными обычным методом наименьших квадратов.

В том случае, если условия Гаусса—Маркова для остаточного члена выполнены, коэффициенты регрессии, построенной обычным методом наименьших квадратов, будут наилучшими линейными несмещенными оценками.

Для того чтобы регрессионный анализ, основанный на обычном методе наименьших квадратов, давал наилучшие из всех возможных результаты, случайный член должен удовлетворять четырем условиям, известным как условия Гаусса—Маркова.

1-е условие Гаусса—Маркова: E(Ut) = 0 для всех наблюдений. Первое условие состоит в том, что математическое ожидание случайного члена в любом наблюдении должно быть равно нулю. Иногда случайный член будет положительным, иногда отрицательным, но он не должен иметь систематического смещения ни в одном из двух возможных направлений.

2-е условие Гаусса—Маркова: Второе условие состоит в том, что дисперсия случайного члена должна быть постоянна для всех наблюдений. Иногда случайный член будет больше, иногда меньше, однако не должно быть априорной причины для того, чтобы он порождал большую ошибку в одних наблюдениях, чем в других. Одна из задач регрессионного анализа состоит в оценке стандартного отклонения случайного члена. Если рассматриваемое условие не выполняется, то коэффициенты регрессии, найденные по обычному методу наименьших квадратов, будут неэффективны.

3- е условие. Это условие предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях. Например, если случайный член велик и положителен в одном наблюдении, это не должно обусловливать систематическую тенденцию к тому, что он будет большим и положительным в следующем наблюдении (или большим и отрицательным, или малым и положительным, или малым и отрицательным). Случайные члены должны быть абсолютно независимы друг от друга.

4-е условие случайный член должен быть распределен независимо от объясняющих переменных. Значение любой независимой переменной в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии. Если это условие выполнено, то теоретическая ковариация между независимой переменной и случайным членом равна нулю. Дело в том, что если случайный член нормально распределен, то так же будут распределены и коэффициенты регрессии.

Предположение о нормальности основывается на центральной предельной теореме. В сущности, теорема утверждает, что если случайная величина является общим результатом взаимодействия большого числа других случайных величин, ни одна из которых не является доминирующей, то она будет иметь приблизительно нормальное распределение, даже если отдельные составляющие не имеют нормального распределения.

4. Оценка достоверности выборочного уравнения регрессии, параметров и прогноза на его основе

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, т.е. оценивает тесноту связи совместного влияния факторов на результат.

Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции. При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:

.

Определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции

При линейной зависимости совокупный коэффициент корреляции можно также определить через матрицу парных коэффициентов корреляции:

,

Для уравнения

определитель матрицы коэффициентов парной корреляции принимает вид:

Определитель более низкого порядка ∆r11 остается, когда вычеркиваются из матрицы коэффициентов парной корреляции первый столбец и первая строка, что соответствует матрице коэффициентов парной корреляции между факторами:

.

Определение коэффициента детерминации (скорректированного, нескорректированного)

Качество построенной модели в целом оценивает коэффициент детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции.

Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле:

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в модель. Формула коэффициента частной корреляции, выраженная через показатель детерминации, для х1 принимает вид:

,

.

Оценка надежности результатов множественной регрессии и корреляции

Оценка значимости уравнения с помощью F-критерия Фишера

Значимость уравнения множественной регрессии в целом, оценивается с помощью F-критерия Фишера по формуле:

При этом выдвигается гипотеза о статистической незначимости уравнения регрессии и показателя тесноты связи.

Если Fфакт. < Fтабл, то гипотезу (Н0) принимаем. С вероятностью 95% делаем вывод о статистической не значимости уравнения в целом и показателя тесноты связи, которые сформировались под неслучайным воздействием факторов х1, х2.

Расчет частных F-критериев

Частные F-критерии оценивают статистическую значимость присутствия факторов х1 и х2 в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т.е. Fх1 оценивает целесообразность включения в уравнение фактора х1 после того, как в него был включен фактор х2. Соответственно, Fx2 указывает на целесообразность включения в модель фактора х2 после фактора х1. Определим частные F-критерии для факторов х1 и х2 по формулам:

Таким образом, низкое значение Fх1факт. свидетельствует о нецелесообразности включения в модель фактора х1

Оценка значимости коэффициентов чистой регрессии по t-критерию Стьюдента

Частный F-критерий оценивает значимость коэффициентов чистой регрессии:

.

5. Понятие гетероскедастичности остатков, тестирование и подходы к устранению. Взвешенный метод наименьших квадратов

Отсутствие гетероскедастичности остатков (гомоскедастичность остатков, т.е. постоянство дисперсий остатков , для любого i, i=1,…,n) – важное условие, которое должно выполняться при использовании метода наименьших квадратов. Чтобы выявить гетероскедастичность остатков выборочной регрессии используют метод проверки статистических гипотез.

В качестве нулевой гипотезы предполагают отсутствие гетероскедастичности в генеральной совокупности. Для ее проверки можно использовать разные тесты: Парка, Уайта, Глейзера, Спирмена, Голдьфельда-Квандта и др.

Методика проверки с помощью критерия Гольдфельда-Квандта заключается в следующем:

1. формулируются гипотезы:

Н₀: ,

Н_А: .

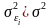2. выбирается уровень значимости ;

3. исходные данные сортируются по величине независимой переменной (по убыванию х);

4. строится уравнение парной линейной регрессии у по х;

5. совокупность делится на три равные части и по первым m набледениям и последним m наблюдениям определим суммы квадратов остатков:

m=12/3=4;

6. рассчитывается фактическое значение критерия Фишера:

7. определяется его критическое значение , где р число параметров уравнения регрессии (для парной линейной регрессии р=2).

8. альтернативная гипотеза о наличии гетероскедастичности будет принята, если:

.

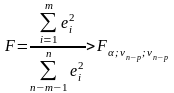Ранг наблюдения переменной - номер наблюдения переменной в упорядоченной по возрастанию последовательности.

• Тест ранговой корреляции Спирмена тест на гетероскедастичность, устанавливающий, что стандартное отклонение остаточного члена регрессии имеет нестрогую линейную зависимость с объясняющей переменной.

При выполнении теста ранговой корреляции Спирмена предполагается, что дисперсия случайного члена будет либо увеличиваться, либо уменьшаться по мере увеличения x, и поэтому в регрессии, оцениваемой с помощью МНК, абсолютные величины остатков и значения х будут коррелированны. Данные по х и остатки упорядочиваются. Если предположить, что соответствующий коэффициент корреляции генеральной совокупности равен нулю, т.е. гетероскедастичность отсутствует, то коэффициент ранговой корреляции имеет нормальное распределение с математическим ожиданием 0 и дисперсией 1/(n - 1) в больших выборках.

Тест Уайта

Предполагается, что дисперсии связаны с объясняющими переменными в виде:

Т.к. дисперсии неизвестны, то их заменяют оценками квадратов отклонений e_i².

Алгоритм применения (на примере трех переменных)

1. Строится уравнение регрессии: и вычисляются остатки.

2. Оценивают вспомогательное уравнение регрессии:

3. Определяют из вспомогательного уравнения тестовую статистику

4. Проверяют общую значимость уравнения с помощью критерия c2.

Замечания

Тест Уайта является более общим чем тест Голдфелда-Квандта.

Неудобство использования теста Уайта: Если отвергается нулевая гипотеза о наличии гомоскедастичности то неясно, что делать дальше.

Обобщенный (взвешенный) метод наименьших квадратов

Наиболее существенным достижением эконометрики является значительное развитие самих методов оценивания неизвестных параметров и усовершенствование критериев выявления статической значимости рассматриваемых эффектов. В этом плане невозможность или нецелесообразность использования традиционного МНК по причине проявляющейся в той или иной степени гетероскедастичности привели к разработке обобщенного метода наименьших квадратов (ОМНК).

Фактически при этом корректируется модель, изменяются ее спецификации, преобразуются исходные данные для обеспечения несмещенности, эффективности и состоятельности оценок коэффициентов регрессии.

Предполагается, что среднее остатков равно нулю, но их дисперсия уже не является постоянной, а пропорциональна величинам Кi, где эти величины представляют собой коэффициенты пропорциональности, различные для различных значений фактора х. Таким образом, именно эти коэффициенты (величины Кi) характеризуют неоднородность дисперсии. Естественно, считается, что сама величина дисперсии, входящая общим множителем при этих коэффициентах пропорциональности, неизвестна.

Исходная модель после введения этих коэффициентов в уравнение множественной регрессии продолжает оставаться гетероскедастичной (точнее говоря, таковыми являются остаточные величины модели). Пусть эти остаточные величины (остатки) не являются автокоррелированными. Введем новые переменные, получающиеся делением исходных переменных модели, зафиксированных в результате i-наблюдения, на корень квадратный из коэффициентов пропорциональности Кi. Тогда получим новое уравнение в преобразованных переменных, в котором уже остатки будут гомоскедастичны. Сами новые переменные — это взвешенные старые (исходные) переменные.

Поэтому оценка параметров полученного таким образом нового уравнения с гомоскедастичными остатками будет сводиться к взвешенному МНК (по существу это и есть ОМНК). При использовании вместо самих переменных регрессии их отклонения от средних выражения для коэффициентов регрессии приобретают простой и стандартизованный (единообразный) вид, незначительно различающийся для МНК и ОМНК поправочным множителем 1/К в числителе и знаменателе дроби, дающей коэффициент регрессии.

Следует иметь в виду, что параметры преобразованной (скорректированной) модели существенно зависят от того, какая концепция положена за основу для коэффициентов пропорциональности Кi. Часто считают, что остатки просто пропорциональны значениям фактора. Наиболее простой вид модель принимает в случае, когда принимается гипотеза о том, что ошибки пропорциональны значениям последнего по порядку фактора. Тогда ОМНК позволяет повысить вес наблюдений с меньшими значениями преобразованных переменных при определении параметров регрессии по сравнению с работой стандартного МНК с первоначальными исходными переменными. Но эти новые переменные уже получают иное экономическое содержание.

Гипотеза о пропорциональности остатков величине фактора вполне может иметь под собой реальное обоснование. Пусть обрабатывается некая недостаточно однородная совокупность данных, например, включающая крупные и мелкие предприятия одновременно. Тогда большим объемным значениям фактора может соответствовать и большая дисперсия результативного признака, и большая дисперсия остаточных величин. Далее, использование ОМНК и соответствующий переход к относительным величинам не просто снижают вариацию фактора, но и уменьшают дисперсию ошибки. Тем самым реализуется наиболее простой случай учета и коррекции гетероскедастичности в регрессионных моделях посредством применения ОМНК.

Изложенный выше подход к реализации ОМНК в виде взвешенного МНК является достаточно практичным — он просто реализуется и имеет прозрачную экономическую интерпретацию. Конечно, это не самый общий подход, и в контексте математической статистики, служащей теоретической основой эконометрики, нам предлагается значительно более строгий метод, реализующий ОМНК в самом общем виде. В нем необходимо знать ковариационную матрицу вектора ошибок (столбца остатков). А это в практических ситуациях, как правило, несправедливо, и отыскать эту матрицу как таковую бывает невозможно. Поэтому приходится каким-то образом оценивать искомую матрицу, чтобы использовать вместо самой матрицы такую оценку в соответствующих формулах. Таким образом, описанный вариант реализации ОМНК представляет одну из таких оценок. Иногда его называют доступный обобщенный МНК.

Следует также учитывать, что коэффициент детерминации не может служить удовлетворительной мерой качества подгонки при использовании ОМНК. Возвращаясь к применению ОМНК, отметим, что достаточную общность имеет метод использования стандартных отклонений (стандартных ошибок) в форме Уайта (так называемые состоятельные стандартные ошибки при наличии гетероскедастичности). Этот метод применим при условии диагональности матрицы ковариаций вектора ошибок. Если же присутствует автокорреляция остатков (ошибок), когда в матрице ковариаций и вне главной диагонали имеются ненулевые элементы (коэффициенты), то следует применять более общий метод стандартных ошибок в форме Невье — Веста. При этом имеется существенное ограничение: ненулевые элементы, помимо главной диагонали, находятся только на соседних диагоналях, отстоящих от главной диагонали не более чем на определенную величину.