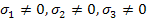17. Внутренние силы. Метод сечений

Тела сопротивляются нагрузке – это обусловлено внутренними силами. Появление внутренних сил, объясняется молекулярным строением материй. Силы в молекуле сцепления сохраняют телу его форму. Воздействие на тело внешних сил вызывает изменение внутренних. Появляются дополнительные внутренние силы, называемые усилием. Величина усилия характеризует способность тела сопротивляться внешним нагрузкам. Усилия, возникающие в телах под действием статических нагрузок, являются уравновешенными. Для определения усилия используют метод сечения.

Пусть на тело действуют статические нагрузки.

1. Мысленно проводим сечение, которое делит тело на 2 части А и В.

2. Условно отбрасываем одну часть, например В.

3. Для компенсации действия отброшенной части к оставшейся части необходимо приложить внутренние силы.

До рассечения тела оно находилось в равновесии. Внутренние силы по отношению к оставшейся части А являются внешними и она должна находиться в равновесии. Для определения внутренних сил используют уравнение статики твёрдого тела.

Приведем систему сил к главному вектору и главному моменту.

Связываем с центром масс сечения систему координат xyz и раскладываем по направлению осей гл. вектор и гл момент.

– продольные силы, нормальные, осевые силы, кот вызывают деформацию растяжения или сжатия.

- поперечные силы, сдвигающие, перерезывающие, вызывают деформацию сдвига.

- крутящий момент, вызывает деформацию кручения.

– изгибающий момент, вызывает деформацию изгиб.

Каждая из этих сил или моментов определяется как сумма проекций соответствующих внешних сил или их моментов на соответствующие оси.

Определяются внутренние силы с использованием уравнений статики, через соответствующие внешние силы, действ на тело.

18. Понятие о напряжениях. Напряженное состояние точки

Поскольку внутренние силы фактически являются распределенными по сечению, то, используя уравнения статики, мы находим лишь их статический эквивалент, т.е. найденные внутренние силы являются равнодействующими действительным внутренними силам, действующим в каждой точке сечения.

Выделим в сечении некоторую точку, бесконечно малую площадку размером dS, на которую действуют внутренние силы. Размеры площадки на столько малы, что внутренние силы на них равны по величине и направлению, их равнодействующая dR, действую в центре масс площадки. Связываем с центром масс сечения систему координат xyz и раскладываем по направлению осей dR. Для определения фактического значения элементарной силы, приходящейся на единицу площади поделим эти проекции на размер площадки.

Напряжение в точке сечения с координатами(x,y,z):

Напряжением называется интенсивность распределения нормальных или поперечных сил, действующих по элементарной площадке в рассматриваемой точке и которая определяется силой приходящейся на единицу площади. В любом теле, через любую точку, можно провести бесконечное число площадок. На них будут действовать и их величина будет зависеть от ориентации площадок.

Под действием внешних сил изменяются внутренние и изменяется расстояние и устанавливается такое расстояние, при которых внутренние силы уравновешивают внешние. Это называется напряженное состояние твёрдого тела. Оно характеризуется совокупностью всех нормальных и касательных напряжений действующих по всем площадкам, которые можно провести через рассматриваемые точки.

Для исследования напряженного состояния выделим в теле элементарный параллелепипед, грани его бесконечно малы, и на них действуют внутренние силы, заменяющие действие отброшенной части и вызывающие напряжение.

Полное напряжение можно разложить на нормальное и касательные составляющие.

При повороте элемента напряжение меняется и можно так его сориентировать, что касательные напряжения будут равны 0.

Грани элемента, на которых отсутствуют касательные напряжения, называются главными площадками, а действующие на них напряжения – главными напряжениями.

В любой точке не менее 3 главных площадок и они взаимно перпендикулярны. Любая точка характеризуется 3-мя главными напряжениями, линии, действия которых определяет 3 главных направления напряженного состояния точки. Их нормируют в порядке убывая .

Различают 3 вида напряженного состояния точки:

1. Линейное (одноосное)

2. Плоское или двухосное

3. Объемное или трехосное