Распределение Стьюдента:

Можно считать, что при К<20, распределение Стьюдента практически идеально совпадает с нормальным распределение. Поэтому при 2<k<20 пользуются распределением Стьюдента, а при больших- распределением Гауса.

Фрагмент таблицы:

Ф(t,k)/k	0.9	0.95	0.98
2	6.314	12.706	31.8
3	2.92	4.303	6.96
6	2.01	2.571	3.36

- коэффициент Стьюдента.

Порядок обработки данных при равноточных измерениях.

Обработка результатов состоит в определении приближенного значения измеряемой величины с указанием ее погрешности.

1. Вычисляют среднее арифметическое результатов измерений:

2. Определяют среднеквадратичное отклонение результатов отдельных измерений:

3. Выявляют промахи.

Промах- погрешность, которая выходит на пределы .

В случае обнаружения промахов их исключают из дальнейшего наблюдения.

4. В случае исключения промахов пересчитывают , .

5. Вычисляют среднеквадратическое отклонение среднего арифметического

n- число наблюдений.

6. Назначают доверительную вероятность Р и по таблице нормального распределения или по таблице распределения Стьюдента определяют доверительный интервал. И результат записывают следующим образом:

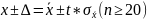
Порядок обработки данных при однократном измерении прибором, погрешность которого известна.

Погрешность прибора может быть задана разными способами:

- Она может быть указана в виде СКО.

- Или в виде класса точности прибора или максимальной погрешности.

1) Погрешность указана в СКО.

Погрешность округления до целого значения шкалы при считывании значений может быть уже включена в эту величину или не включена.

Если погрешность уже включена:

Если погрешность не вклченат в , то результирующий СКО определяют следующим образом:

Значение дисперсии погрешности округления определяются в предположении, что погрешность округления имеет равномерное распределение.

Дисперсия округления:

- величина цены деления шкалы.

2) Погрешность прибора указана в виде класса точности или максимальной погрешности( ).

В этом случае значение СКО нельзя определить однозначно и для ее нахождения делают дополнительные допущения.

Считают что d=3 .

Назначают доверительную вероятность Р и по таблице нормального распределения находят значения доверительного интервала.

Результат записывают в виде:

Обработка результатов косвенных измерений.

Допустим, что известны результаты прямых измерений величин x₁,x₂…..x_q, известны погрешности этих величин и они имеют систематические и случайные составляющие:

Требуется найти погрешность величины Y:

Y=F(x₁,x₂,……..,x_q)

Поскольку погрешности малы с измеряемыми величинами, то при из расчете ограничиваются членами первой степени.

- сумма частн. Производных «х» на значение соответствующей погрешности.

Поскольку математическое ожидание суммы равно сумме математических ожиданий, то математическая погрешность определяется по формуле:

Принято рассчитывать систематическую погрешность для случая, когда все частные систематические погрешности имеют одинаковый знак.

Итоговая систематическая погрешность:

Остаются случайные составляющие погрешности.

Порядок достаточно сложен. Наиболее простой он тогда, когда велики x_i статически независимы, в этом случае дисперсия определяется из соотношения: