Случайные погрешности.

При повторных измерениях этот вид погрешностей принимает различные значения, образуя случайный ряд чисел. Обозначается 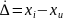. Если систематическая погрешность отсутствует, то можно показать что при N контрольных наблюдениях измеряемой величины, среднее арифметическое величины X будет стремится к истинному значению . Наиболее полной характеристикой случайной величины является ее функция плотности распределения вероятности. В зависимости от вида этой функции различают разные законы распределения случайной величин Х.

Р- вероятность. Помимо функции распределения вероятностей для описания свойств случайных величин используют математическое ожидание и дисперсию.

Эта величина равна наиболее вероятному значению изменяемого параметра. Если систематическая погрешность при измерении отсутствует, то математическое ожидание совпадет с истинным значением измеряемой величины.

Элементы теории погрешностей.

В зависимости от характера проявления, причин возникновения, а так же способов учета или исключения, все погрешности измерений можно разделить на 3 группы: случайные, систематические и грубые погрешности( промахи).

Случайная погрешность- составляющая погрешности измерений, изменяющаяся случайно при повторных измерениях одной и той же величины. Причины из возникновения не известны или их невозможно учесть. Они обусловлены случайными факторами.

Систематическая погрешность - погрешности, которые остаются постоянными или закономерно изменяются при повторных измерениях.

Грубые погрешности- погрешности измерений, существенно отличающиеся от обычных в данных условиях. Они возникают под влиянием неожиданного увеличения одного из случайных факторов.

По причине возникновения погрешности можно разделить на инструментальные, погрешности установок, внешних влияний, методические и субъективные.

Инструментальные погрешности обусловлены несовершенством инструментальных средств. Примеры: погрешности из-за неточности нанесения делений на отсчетную шкалу, погрешности из-за люфтов и износа деталей.

Погрешность установок возникает при работе приборов в неправильном положении или из-за несогласованности характеристик приборов, составляющих измерительную установку.

Погрешности внешних влияний появляются в связи с тем, что на работу прибору или количество меры могут оказать влияние температура окружающей среды, влажность, давление, вибрация, воздушные потоки, электрические и магнитные поля.

Методические( теоретические погрешности) возникают в следствии недостаточной разработки теории метода измерений, а так же от упрощений, допускаемых при проведении измерений. Пример: подключение вольтметров с недостаточной чувствительностью( или, что тоже самое, малым внутренним сопротивлением) может существенно изменить распределение токов и напряжений в исследуемой схеме.

Субъективные погрешности обусловлены индивидуальными особенностями оператора.

Случайные погрешности.

Причин, вызывающих погрешности, может быть много, а влияние каждой из них мало и изменчиво. В этом случае погрешность является случайной. Устранить случайные погрешности невозможно, но существуют методы их оценки, основанные на теории вероятность и математической статистике. Задача оценки погрешности результата измерения состоит в том, чтобы охарактеризовать неопределенность полученного результата, т.е. указать границы изменения погрешностей результата измерения при повторных измерениях.

Наиболее полной характеристикой случайной погрешности как и любой случайной величины является закон распределения вероятности, определяющий возможные значения случайной погрешности и вероятность ее появления. В большинстве физических измерений случайные погрешности подчиняются закону нормального распределения или закону Гаусса. Случайную погрешность _i можно представить как разность между результатом измерения и математических ожиданием М[х], которая при отсутствии систематических погрешностей принимается за истинное значение измеряемой величины.

Плотность нормального распределения вероятности случайных погрешностей или дифференциальная функция нормального распределения P(x) выражается формулой Гаусса:

- случайная абсолютная погрешность; - среднее квадратическое отклонение;

Величина ² называется дисперсией случайной погрешности. Дисперсия представляет собой математическое ожидание квадрата случайной погрешности, характеризуя разброс результатов измерения из-за наличия случайной погрешности. В теории вероятностей эта величина называется вторым центральным моментом.

Заметим что математическое ожидание, статистическим аналогом которого является среднее арифметическое, в общем случае не равно истинному значению измеряемой величины при конечном количестве измерений. При N-> и отсутствии систематической погрешности М[x]->Х₀. Вместе с нормальным законом распределения случайной величины могут иметь место и другие законы распределения: равномерный, треугольный, трапецеидальный. Примерами случайных погрешностей с равномерным распределением являются погрешности обусловленные сухим трением в опорах стрелочного прибора, погрешности отсчета по равномерной шкале аналоговых приборов, погрешности цифрового отсчета.

Дисперсию для этих распределений можно определить по приведенной выше формуле, рассчитав предварительно P(x) с использованием свойства:

Для равномерного закона: P(x)= const.

Подставляя это значение в формулу для дисперсии получим:

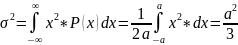
Аналогичным образом можно определить дисперсию среднего квадратического отклонения для треугольного и трапецеидального закона. На пример для треугольного закона: