Т 10 Параллельность и перпендикулярность прямых и плоскостей в пространстве
1. Основные аксиомы стереометрии
Основные фигуры: точка, прямая, плоскость
В
.
А
А
а
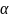β
Аксиома 1: Какова бы ни была плоскость существуют точки принадлежащие ей и точки не принадлежащие ей
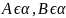
Аксиома 2: Если две плоскости имеют общую точку, то они пересекаются по прямой содержащую все общие точки
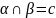
β А є £; A є β →A є C
Аксиома 3: Через две пересекающиеся прямые можно провести плоскость и причем только одну
а а
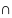в→ а є
; в є
- единственна
в
Теорема 1: Через прямую и точку не принадлежащую этой прямой можно провести плоскость и причем только одну.
А
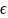а → a є
; А є
-единственная
Теорема 2: Через три точки не лежащие на одной прямой можно провести плоскость и причем только одну.
А,В,С не лежат на прямой → A;B;Cє
А
. В.
-единственная
С.
Теорема 3: Если две точки прямой принадлежат плоскости, то вся прямая принадлежит плоскости то есть, любая точка прямой принадлежит этой плоскости
А,В є
а
А : В є a → a є
В
А
Аксиома 4: Любая плоскость делит пространство на два полупространства. Если концы отрезка принадлежат одному полупространству, то отрезок не пересекает плоскость. Если концы отрезка принадлежат различным полупространствам, то отрезок пересекает плоскость.
XY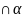
ZF = A
Замечание: все теоремы, аксиомы планиметрии верны и в пространстве.
Например: через две точки можно провести одну прямую, как на плоскости
так и в пространстве.
