Вариант 16.
Найти общее решение дифференциальных уравнений:
-
а) ;
в) ;
б) ;
г) .
д)
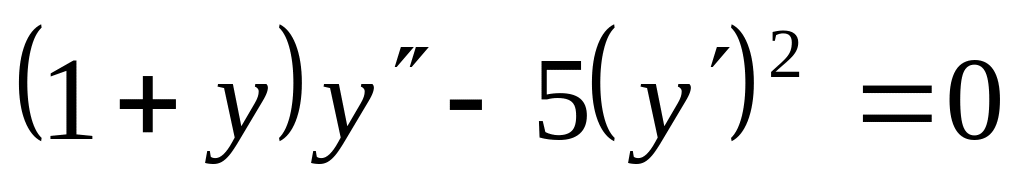
е)
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
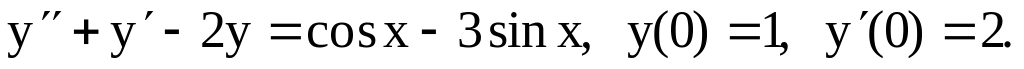
Составить дифференциальное уравнение по заданному семейству интегральных кривых
.
Найти общее решение системы дифференциальных уравнений .
Катер движется в спокойной воде со скоростью
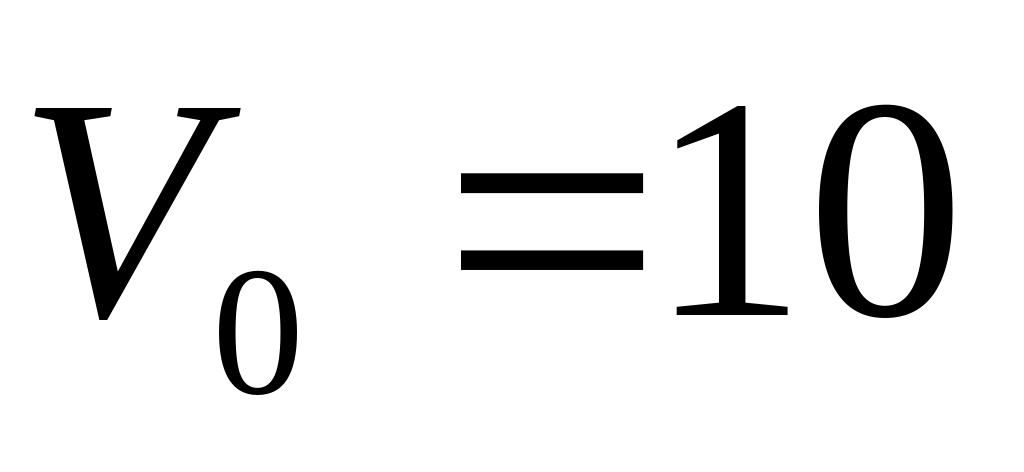км/час. На полном ходу его мотор был
выключен, и, через 2 мин, скорость катера
уменьшилась до
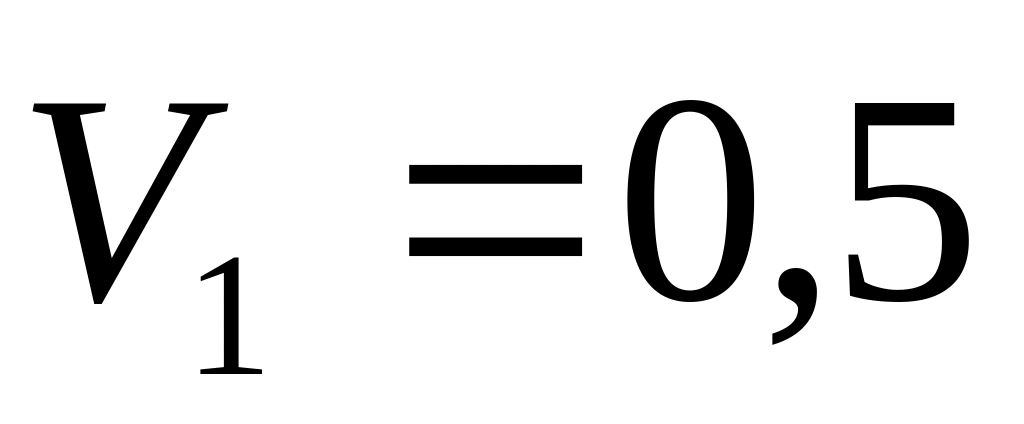км/час. Найти
скорость, с которой двигался катер
через 40 секунд после выключения мотора,
считая, что сопротивление воды
пропорционально скорости движения
катера.
Определить закон и период колебаний маятника в среде с сопротивлением, пропорциональным скорости линейной качания.
Зауваження до виконання завдання.
1. Завдання оформити на листах формату А4.
2. Перевірку отриманих розв’язків рівнянь виконати у середовищі Mathcad.
3.Побудувати у середовищі Mathcad графіки функцій, що є розв’язками у завданнях 2 та 5.
4. Відповідь у завдвнні 6 отримати у загальному вигляді, а потім виконати розрахунок, надавши всім величинам правдоподібні значення та побудувати графіки для отриманих функцій.
5. Файлу з перевіркою та графіками дати назву
Призвище.xvcd
та розмістити у папці за адресою Група/Математика/ЛР6
Вариант 17.
Найти общее решение дифференциальных уравнений:
-
а)
;в)
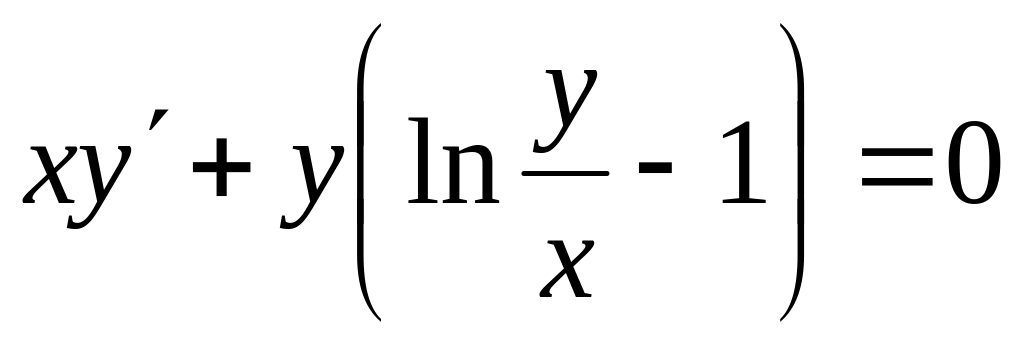;б) ;
г) .
д)
е)
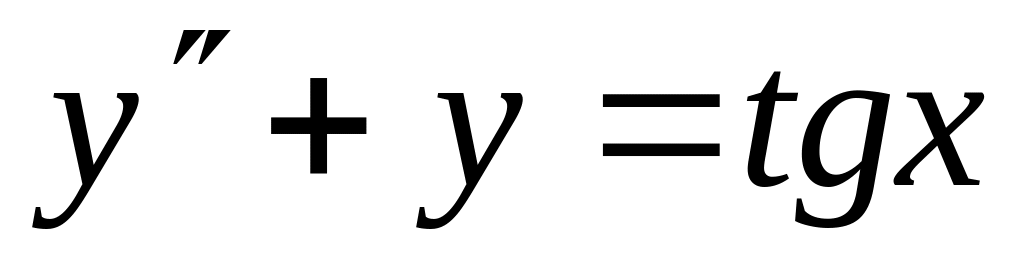
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
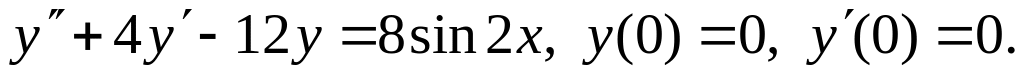
Составить дифференциальное уравнение по заданному семейству интегральных кривых
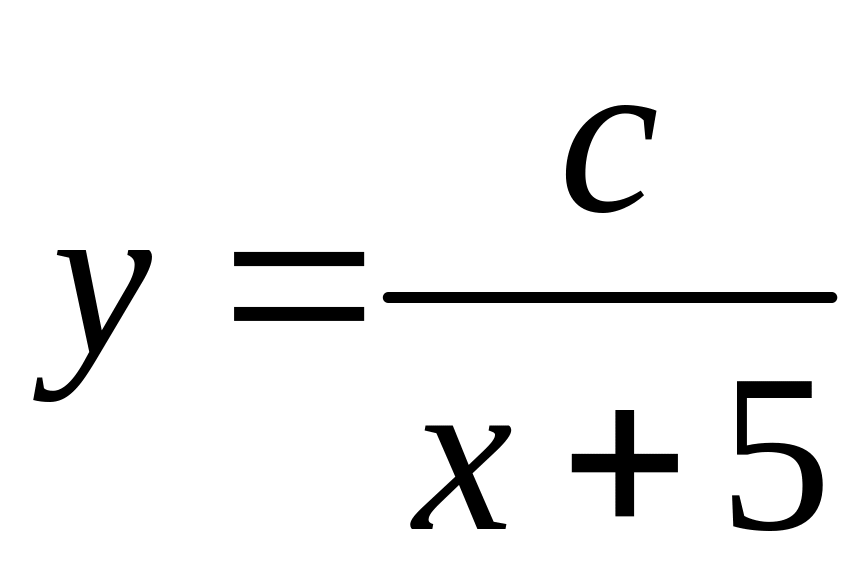
Найти общее решение системы дифференциальных уравнений .
Найти уравнение кривой, проходящей через точку A(3,1) и, обладающей тем свойством, что отрезок касательной между точкой касания и осью ОХ делится пополам в точке пересечения с осью ОУ.
Определить закон движения материальной частицы массой m под влиянием силы, напрвленной к центру О и прямо пропорциональной удалению частицы от центра притяжения.
Зауваження до виконання завдання.
1. Завдання оформити на листах формату А4.
2. Перевірку отриманих розв’язків рівнянь виконати у середовищі Mathcad.
3.Побудувати у середовищі Mathcad графіки функцій, що є розв’язками у завданнях 2 та 5.
4. Відповідь у завдвнні 6 отримати у загальному вигляді, а потім виконати розрахунок, надавши всім величинам правдоподібні значення та побудувати графіки для отриманих функцій.
5. Файлу з перевіркою та графіками дати назву
Призвище.xvcd
та розмістити у папці за адресою Група/Математика/ЛР6
Вариант 18.
Найти общее решение дифференциальных уравнений:
-
а)
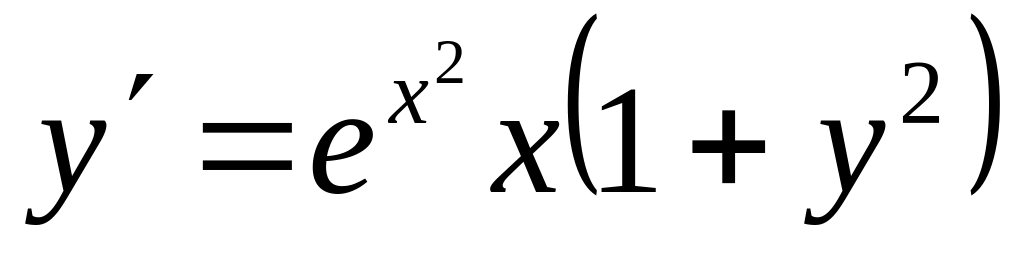;в)
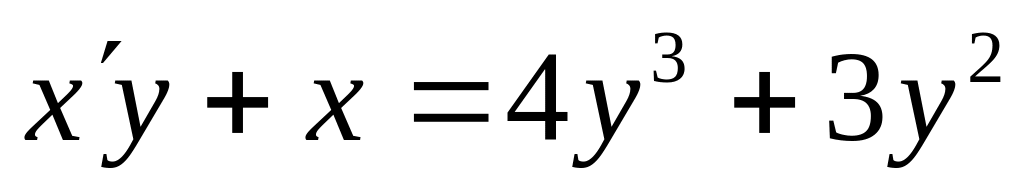;б)
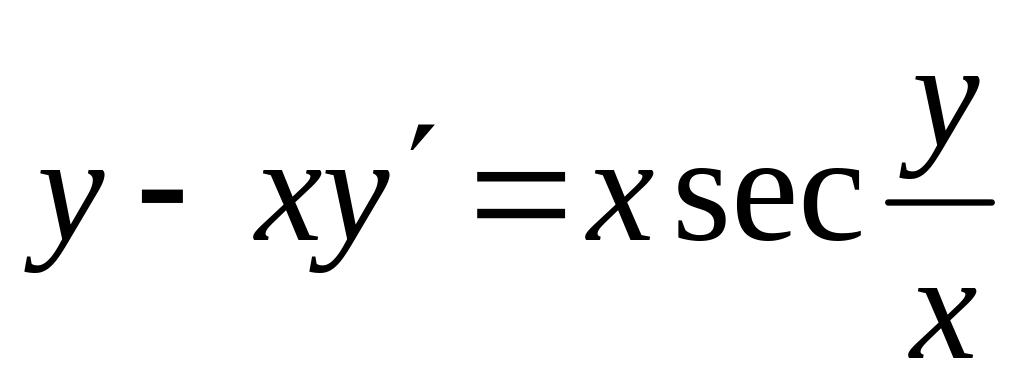;г) .
д)
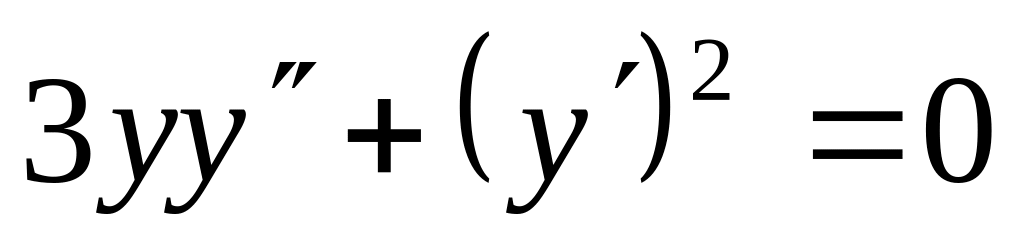
е)
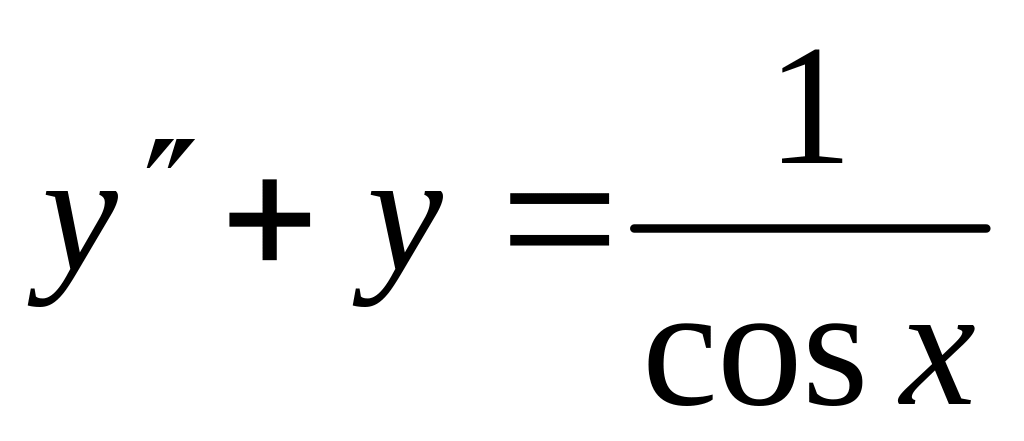
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
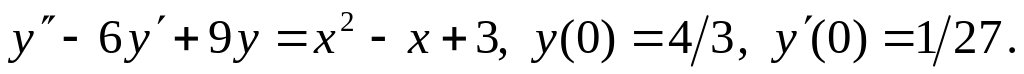
Составить дифференциальное уравнение по заданному семейству интегральных кривых
.
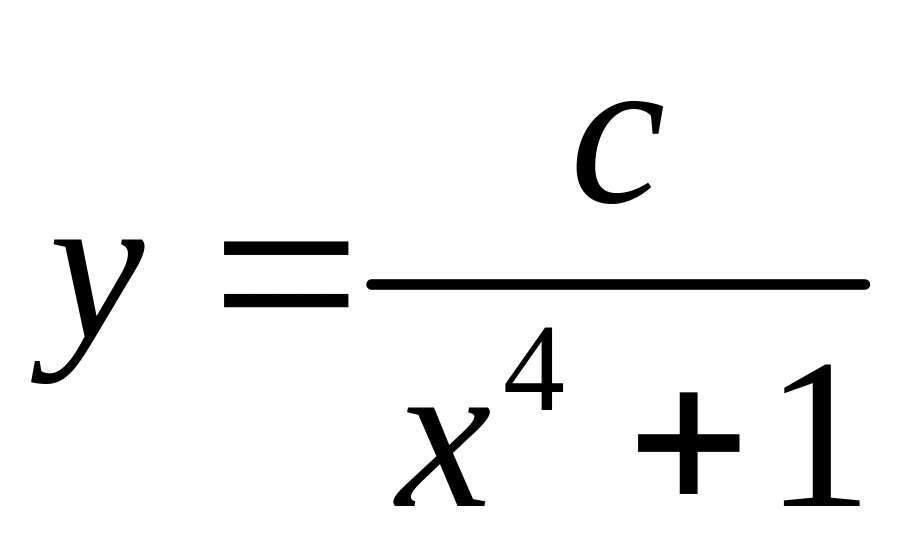Найти общее решение системы дифференциальных уравнений
.
Найти уравнение кривой, проходящей через точку B(1, 0) и, обладающей тем свойством, что отрезок, отсекаемый касательной на оси ОУ, равен радиус-вектору точки касания.
Допустим, что через земной шар проложен узкий трубопровод, проходящий через центр Земли. Упавший в него камень притягивается центром Земли с силой, прямо пропорциональной расстоянию между ними. Через какое время камень пролетит сквозь всю Землю?
Зауваження до виконання завдання.
1. Завдання оформити на листах формату А4.
2. Перевірку отриманих розв’язків рівнянь виконати у середовищі Mathcad.
3.Побудувати у середовищі Mathcad графіки функцій, що є розв’язками у завданнях 2 та 5.
4. Відповідь у завдвнні 6 отримати у загальному вигляді, а потім виконати розрахунок, надавши всім величинам правдоподібні значення та побудувати графіки для отриманих функцій.
5. Файлу з перевіркою та графіками дати назву
Призвище.xvcd
та розмістити у папці за адресою Група/Математика/ЛР6