Вариант 1.
Найти общее решение дифференциальных уравнений:
-
а)
;в)
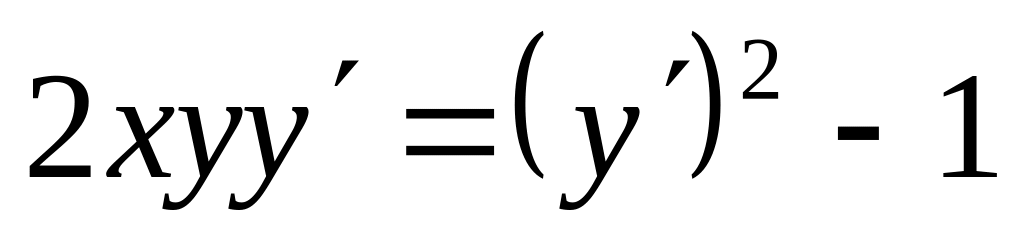;б)
;г)
;д)
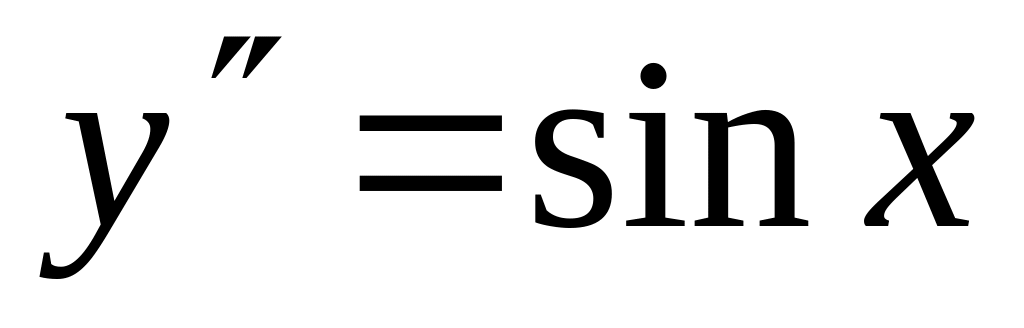;д)
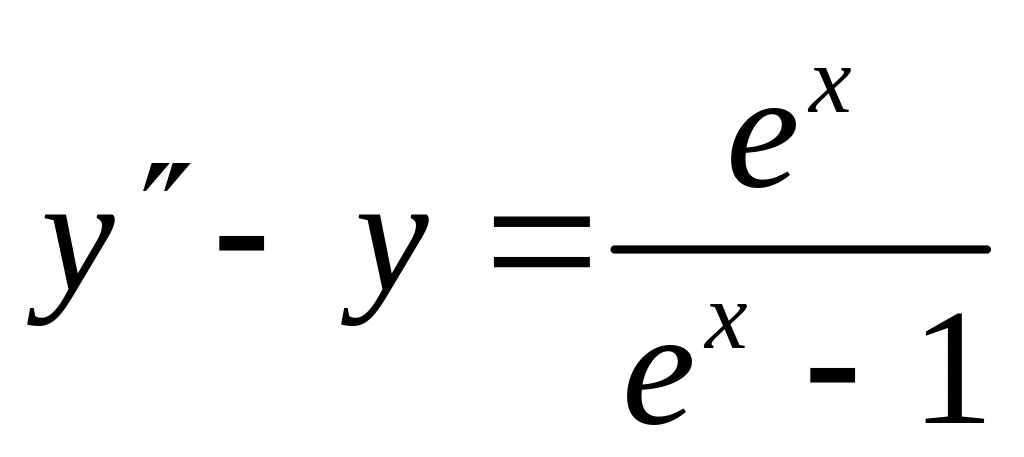
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
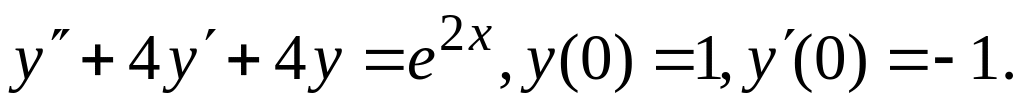
Составить дифференциальное уравнение по заданному семейству интегральных кривых
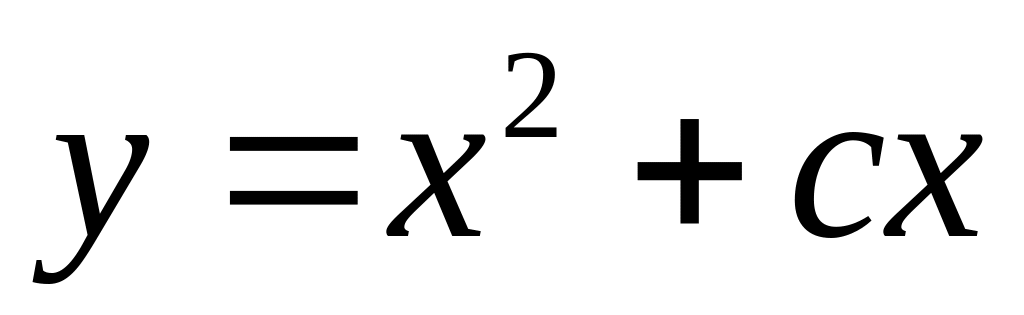.Найти общее решение системы дифференциальных уравнений
.
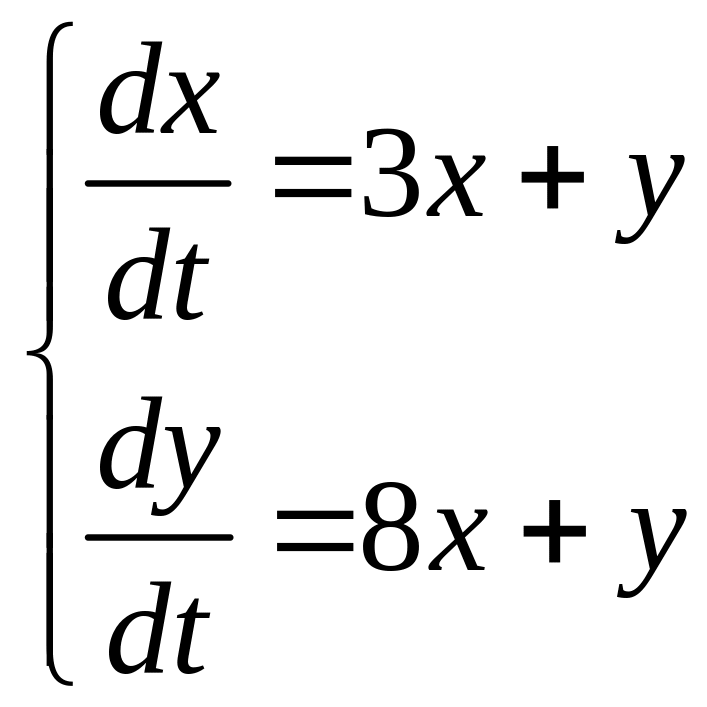Записать уравнение кривой, проходящей через точку
,
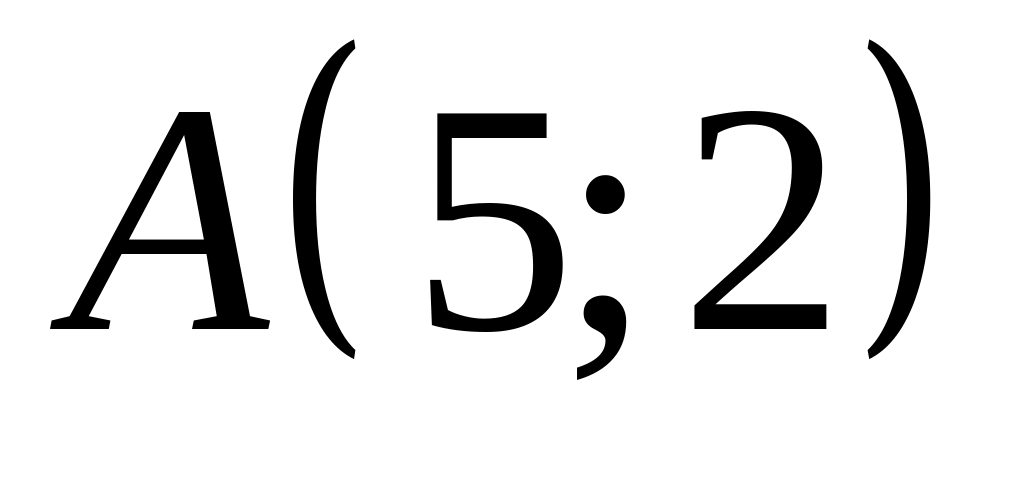если известно, что угловой коэффициент
касательной в любой ее точке в 3 раз
больше углового коэффициента прямой,
соединяющей точку А с началом координат.При размыкании электрической цепи сопротивление цепи R быстро возрастает от первоначальной величины R0 до бесконечности. На основании опыта допускают, что зависимость R от t в этом процессе выражается
,
где
- время всего процесса размыкания. Найти
силу тока в любой момент в цепи при
постоянной электродвижущей силе E
и самоиндукции L.
Зауваження до виконання завдання.
Завдання оформити на листах формату А4.
Перевірку отриманих розв’язків рівнянь виконати у середовищі Mathcad.
Побудувати у середовищі Mathcad графіки функцій, що є розв’язками у завданнях 2 та 5.
Відповідь у завдвнні 6 отримати у загальному вигляді, а потім виконати розрахунок, надавши всім величинам правдоподібні значення та побудувати графіки для отриманих функцій.
Файлу з перевіркою та графіками дати назву
Призвище.xvcd
та розмістити у папці за адресою Група/Математика/ЛР6
Вариант 2.
Найти общее решение дифференциальных уравнений:
-
а)
;в)
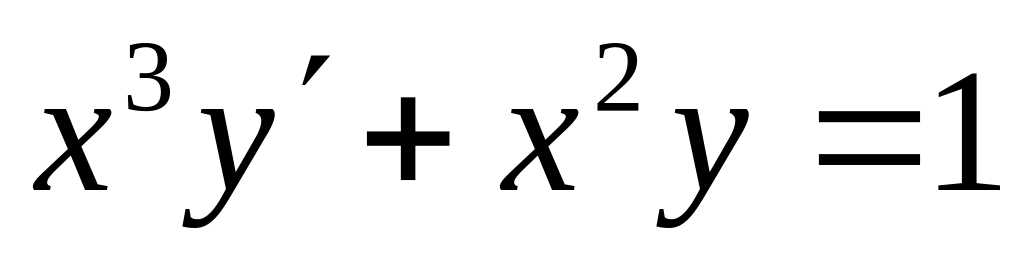;б)
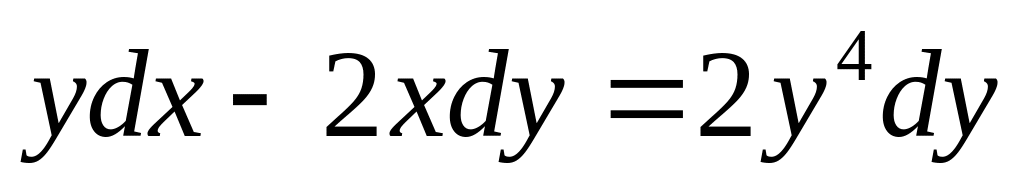;г)
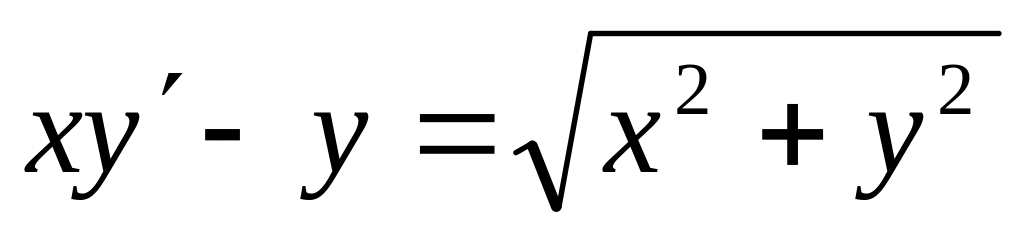.д)
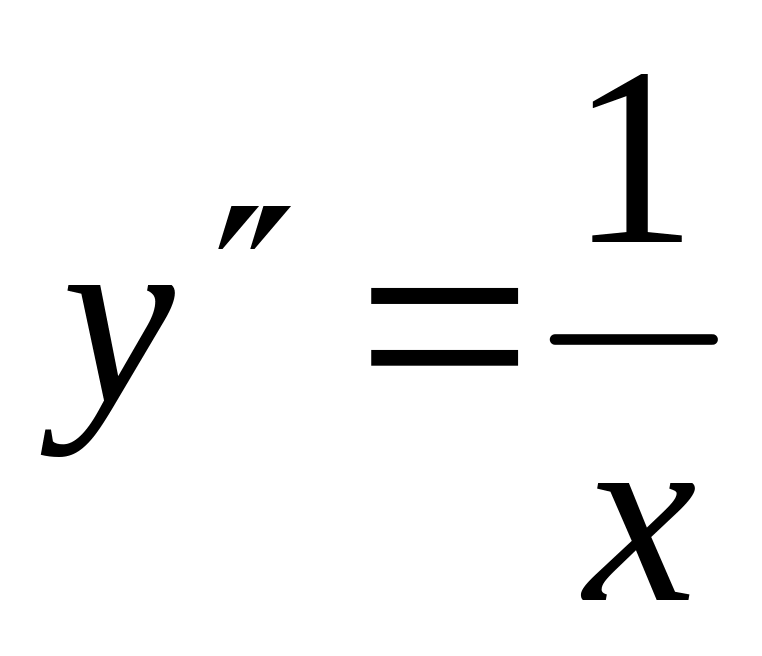
е)
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
Составить дифференциальное уравнение по заданному семейству интегральных кривых
.
Найти общее решение системы дифференциальных уравнений
.
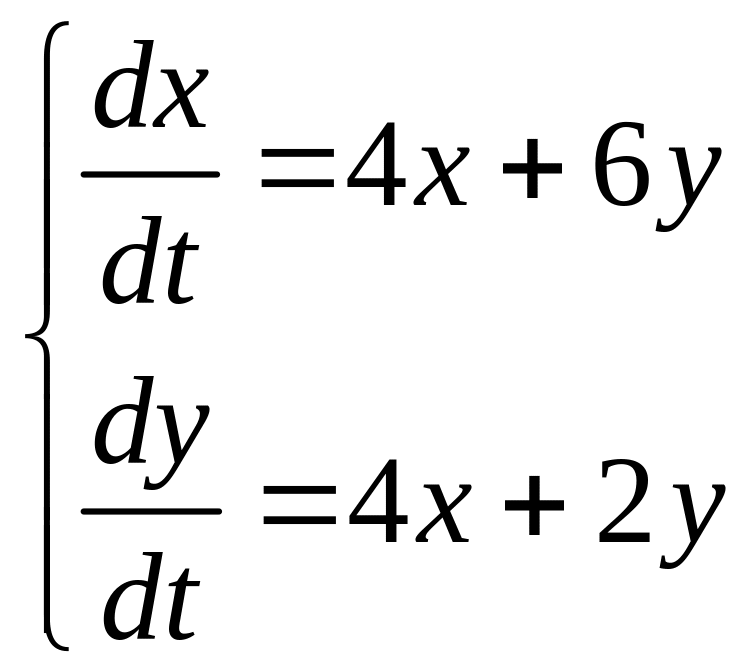Найти уравнение кривой, проходящей через точку A(10, 10) и, обладающей тем свойством, что отрезок, отсекаемый на оси абсцисс касательной, проведенной в любой точке кривой, равен кубу абсциссы точки касания.
В цепи поддерживается напряжение E. Сопротивление цепи R. Коэффициент самоиндукции L. За какое время с момента замыкания цепи возникший в ней ток достигнет 99 % своей предельной величины?
Зауваження до виконання завдання.
1. Завдання оформити на листах формату а4.
2. Перевірку отриманих розв’язків рівнянь виконати у середовищі Mathcad.
3.Побудувати у середовищі Mathcad графіки функцій, що є розв’язками у завданнях 2 та 5.
4. Відповідь у завдвнні 6 отримати у загальному вигляді, а потім виконати розрахунок, надавши всім величинам правдоподібні значення та побудувати графіки для отриманих функцій.
5. Файлу з перевіркою та графіками дати назву
Призвище.xvcd
та розмістити у папці за адресою Група/Математика/ЛР6