Анализ различных уравнений прямой на плоскости.

Общее уравнение прямой:

Уравнение прямой, проходящей через заданную точку:

Векторное параметрическое уравнение прямой:

Определение: любой ненулевой вектор 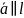называется направляющим вектором этой прямой .

Замечание: любая прямая полностью определяется одной точкой и направляющим вектором.

О – начало координат.

Если ,

П рировняв координаты уравнения получим параметрические уравнения прямой (несколько координат)

Пусть

Тогда АСК

Система двух уравнений (2) эквивалентна уравнению (1).

Механическая интерпретация уравнения (1): движение по прямой в направлении вектора , где - время.

Получим из системы уравнений (2) канонические уравнения: исключим параметр из системы уравнений (2)

( 3) – каноническое уравнения прямой, где координаты произвольной точки, – координаты фиксированной точки на прямой, – координаты направляющего вектора.

Уравнение прямой, проходящей через 2 точки.

Если известны 2 точки на прямой

- направляющий вектор.

Из уравнения (3) получаем уравнение (4)

Векторное уравнение прямой, не содержащей параметр.

Л юбая прямая определяется одной точкой и перпендикулярным вектором – нормальным вектором прямой.

Берем произвольную точку . ( - фиксированная)

Условие параллельности:

Уравнение (5) называется векторным уравнением прямой.

Возьмём параметрическое уравнения прямой (1) и запишем его без параметра:

АСК

Запишем уравнение (5) через координаты получим ДПСК:

Пусть координаты

Из уравнения (5) получим:

(7) - уравнение прямой, проходящей через точку перпендикулярно вектору .

Если прямая в ДПСК, то - координаты нормального вектора.

У равнение прямой с угловым коэффициентом.

Возьмём вектор - единичным

В ДПСК: вектор с осью образует угол

Тогда

- угловой коэффициент прямой.

Уравнение прямой через точку и заданным

Нормальное уравнение прямой в ДПСК.

В озьмём нормальный единичный вектор

- расстояние от точки О до прямой .

Выразим уравнение прямой через и .

Возьмём произвольную точку , и найдём ортогональную проекцию вектора

Найдём в ДПСК:

Если прямая проходит через начало:

Следствие (расстояние от точки до прямой):

о т до прямой

Расстояние

Приведение общего уравнения прямой к нормальному в ДПСК.

– единичный нормальный вектор

; ;

Следствие: расстояние от точки до прямой

Алгебраические линии второго порядка на плоскости.

Распишем уравнение 1 без знака суммирования:

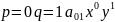
Окружность.

Определение: окружность – это множество точек плоскости (геометрическое место точек), которые находится находятся на заданном расстоянии (радиус) от заданной точки (центр).

Пусть – начало координат, – окружность.

- уравнение окружности

Свойство симметрии относительно оси:

симметричны относительно

симметричны относительно

Эллипс.

Определение: эллипс – это геометрическое место точек плоскости, сумма расстояний которых от двух заданных точек в плоскости (фокус) есть величина постоянная.

Возьмём 2 точки и

Множество не пусто, если :

эллипс.

Исходя из получим уравнение эллипса в ДПСК:

– середина , ось содержит

- уравнение эллипса

Теорема: уравнение равносильно уравнению , где

Доказательство:

2)

Из уравнения следует

Так как и

Свойства:

• Эллипс имеет 2 оси симметрии, и , и центр симметрии Если , то и симметричны относительно симметричны относительно симметричны относительно

• Эллипс расположен в прямоугольнике следует Точки , - вершины эллипса

• Эксцентриситет эллипса

• Э ллипс можно получить равномерным сжатием окружности из вдоль оси с коэффициентом сжатия Покажем, что По условию

• П араметрическое уравнение эллипса За основу берем окружность радиуса , с центром в начале координат; воспользуемся тем, что эллипс получается сжатием , ,

• Прямые называются директрисами эллипса отношение расстояния от этой точки до фокуса к расстоянию до соответствующей директрисы есть величина постоянная и она равна :

Гипербола – это геометрическое место точек плоскости, разность расстояний которого до двух заданных точек плоскости (фокусы) есть величина постоянная.

При этом

Выводим уравнение гиперболы:

Введем ДПСК, – середина отрезка и начало координат.

Теорема:

Доказательство: 1)

2)

Рассмотрим

Свойства гиперболы:

• Гипербола имеет 2 оси симметрии и центр симметрии Если , то и симметричны относительно симметричны относительно симметричны относительно

• Гипербола располагается в области Исходя из уравнения

• Покажем, что и являются наклонными асимптотами, в силу симметрии достаточно доказать для первой четверти. Прямая линия называется асимптотой для , если при погранично приближается к . Взяли точку , Докажем, что при , тогда (так как )