Проекции точек и векторов.

Определение: пусть на плоскости П заданы две непараллельные прямые m и n; пусть P П. Через Р проведем прямую k параллельную m при P m или совпадающую с m при P m. Тогда пересечение прямых k и n называется проекцией точки Р.

Определение: пусть в пространстве заданы плоскость m, прямая n, точка P в пространстве; проекцией Р на прямую n, параллельную плоскости m, называется пересечение плоскости k, содержащей точку Р , параллельной [совпадающей с] m с прямой n.

Определение: пусть в пространстве заданы прямая m и плоскость n ; проекцией точки Р на плоскость n параллельной прямой m называется точка пересечения прямой k||m с плоскость n.

Ортогональной проекцией во всех трёх случаях точки Р называется такая проекция, когда m ортогонально n.

Возьмём вектор ;

рассмотрим и ;

проекцией вектора на n параллельно m называется вектор

Определение: величиной проекции вектора f на ось n параллельно m называется

Теорема:

1. 

2. 

Доказательство:

1. 

=

2. , ; по теорема Фалеса

Проекции точек и векторов. Свойства проекций.

Пусть – произвольный вектор. тогда проекция :

Теорема 1:

1. Пусть на плоскости I; пусть – произвольный вектор, , тогда

2. Пусть в пространстве задан базис: , тогда

3. Пусть в пространстве задан базис: , тогда

Доказательство:

1. - параллелограмм, , , - компланарны: , и - компланарные: , . Из единственности координат следует, что

2. - параллелограмм, , , - компланарны: , в плоскости, параллельной m, значит раскладывается по её базису: , . Из единственности координат следует, что

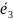
3. - параллелограмм, , , параллелен плоскости n, параллелен вектору . Из единственности координат следует, что

Следствия:

1. Равные векторы имеют равные проекции.

2. Свойства проекций:

   1. Проекция суммы:

   2. Проекция вектора, умноженного на число

Доказательство:

1. Пусть ;

2. Пусть тогда ,

Величина проекции вектора на ось n:

Замечание:

• ,

• ,

Теорема 2:

1. 

2. 

Доказательство:

1. ,

2. 

Ортогональная проекция вектора на вектор это или ортогональная проекция вектора на ось с базисным вектором . В еличина ортогональной проекции вектора на вектор это 0, если = или

Углом между двумя ненулевыми векторами и это 0⁰ , 180⁰ , или угол АОВ, если

Теорема 3: о величине ортогональной проекции

1. Величина ортогональной проекции ненулевого вектора на ось n равна , где угол между вектором и осью n

2. Величина ортогональной проекции ненулевого вектора на ненулевой вектор равна

Доказательство:

Пусть вектор и ось n коллинеарные:

• если , то , тогда ;

• если , то , тогда .

Пусть вектор и ось n неколлинеарные;

• ; по определению , по формуле ;

• 

• ,