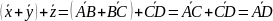Аналитеская геометрия

Векторы. Понятие вектора.

Отрезок прямой задаётся его двумя равноправными точками, его концами.

Определение: Направленный отрезок- это отрезок, определяемый двумя точками с указанием, какая из них первая, начало, и какая вторая, конец. Нулевой направленный отрезок – тот, у которого начало и конец совпадают. Его направление не определено, параллелен любой прямой и плоскости.

Определение: Вектором называется направленный отрезок.

Длина вектора – длина соответствующего отрезка.

Определение: Векторы называются

• Коллинеарными, если они расположены на одной или параллельных прямых

• Компланарными, если они расположены в одной или на параллельных плоскостях.

Определение: про коллинеарные можно сказать одинаково они направлены или противоположно направлены.

Ненулевые векторы и называют

• одинаково направленными

  • отрезки AB и A’B’ лежат на одной прямой

отрезок AB принадлежит лучу с началом в точке А; отрезок A’B’ принадлежит лучу с началом в точке A’, то есть

или

• отрезки AB и A’B’ лежат на параллельных прямых

точки BB’ лежат по одну сторону от прямой AA’ (BB’ не пересекает AA’)

• в противном случае их называют противоположно направленными

Операции сложения векторов и умножение вектора на число. Свойство операций.

Определение: пусть заданы векторы и . Отложим и . Суммой векторов и называется вектор ( ).

Операция, сопоставляющая для и , называется сложением.

Определение: произведение вектора на число называется вектор ( ) удовлетворяющий условиям:

• 

• при при

• При

Операция, сопоставляющая числу и вектору вектор называется произведением вектора на число.

Сложение векторов и умножение векторов на числа называют линейными операциями.

Теорема (свойства линейных операций): множество векторов является линейным пространством со сложением векторов и умножением векторов на вещественные числа. Таким образом выполнены 8 аксиом:

1. 

2. 

3. , – противоположенный, единственный

4. 

5. 

6. 

7. 

8. 

Доказательство:

Возьмём векторы следующим образом ; ;

1. 

6. 

7. 

8. =

Следствия:

• Нулевой элемент единственный

• 

• 

Линейная комбинация. Линейная зависимость и независимость векторов.

Определение: – линейное пространство

n N α₁, α₂,…, α_n R

, ,…,

Вектор α₁ + α₂ +… +α_n – называется линейной комбинацией векторов , ,…,

Числа α₁, α₂,…, α_n – коэффициенты линейной комбинации.

Линейная комбинация называется тривиальной, если все α₁, α₂,…, α_n равны 0 и нетривиальной в противном случае.

Определение: векторы , ,…, называются линейно независимыми, если только их тривиальная линейная комбинация равна нулевому вектору.

Векторы , ,…, называются линейно зависимыми, если существует нетривиальная линейная комбинация, равная нулевому вектору

Теорема (критерий линейной зависимости):

Пусть есть , ,…, . Эти векторы линейно зависимы тогда и только тогда, когда один из векторов линейно выражается через остальные (является линейной комбинацией других векторов).

Следствие: , ,…, – линейно независимы тогда и только тогда, когда ни один из векторов линейно не выражается через остальные (не является линейной комбинацией остальных).

Теорема: ряд признаков зависимости и независимости:

1. При изменении порядка векторов их линейная зависимость и независимость сохраняется.

2. Один вектор линейно зависим тогда и только тогда, кода он нулевой.

3. Если часть векторов линейно зависима, то и все векторы линейно зависимы.

4. Если среди векторов есть нулевой, то они линейно зависимы.

5. Векторы , ,…, E линейно зависимы тогда и только тогда, когда =0 \/ выражается через предыдущие.

Следствия:

1. Если все векторы линейно независимые, то и любая их часть тоже линейно зависимая.

2. Ненулевые векторы линейно независимые тогда и только тогда, когда ни один из векторов линейно не зависим от других ( не является линейной комбинацией предыдущих).

3. Если векторы , ,…, линейно независимые, а , ,…, , линейно зависимые, то линейно выражается через , ,…,

Лемма 1: пусть произвольный. Тогда любой вектор коллинеарный линейно выражается через

при , Доказательство:

1. Если , то

2. Если вычислим такое

, по определению: 1)

2) по условию

3. Если вычислим такое

, по определению: 1)

2)

Теорема:

1. Пусть -прямая и любой вектор, параллельный , тогда каждый вектор из множества линейно выражается через , т.е.

2. Пусть П - плоскость и - не коллинеарные векторы, параллельные ей, тогда каждый вектор из множества линейно выражается через ,

т.е.

3. Пусть , некомпланарные векторы, тогда каждый вектор из множества линейно выражается через , ,

т.е.

Доказательство:

1. Если

По лемме 1

2. Переносим векторы в плоскость П

Если , то Если

Проведем через точку O , содержащую , , через точку M проводим прямую, параллельную до пересечения с в точке N. , по условию

По определению

по пункту 1: согласно Лемме

3. Все векторы откладываем от точки О

Плоскость П содержит точку О и , проводим прямую из М параллельную до П (точка N)

проводим прямую из N параллельную до (точка К)

Теорема (о линейной зависимости):

1. Один вектор линейно зависим он нулевой

2. Два вектора линейно зависимы они коллинеарны

3. Три вектора линейно зависимы они компланарны

4. Четыре и более векторов всегда линейно зависимые

Доказательство:

1. - линейно зависим при – комбинация тривиальная

2. Пусть и - линейно зависимые Если или то или линейно зависим (по п.1) они коллинеарны Если то по определению

Пусть По предыдущей теореме один вектор выражается через остальные они линейно зависимые

3. Пусть , - линейно зависимые а)Если есть хоть один , то они параллельны некоторой плоскости – компланарны б) если есть пара коллинеарных ( отсутствует) Все три коллинеарны, есть сколько угодно плоскостей, которым они параллельны. Если только 2 коллинеарны: отложим 2 вектора от одной точки, построим плоскость параллельную им, и третий вектор, параллельный одному из двух двугих. в) , - линейно зависимые, среди них нет и нет компланарных какой-то вектор выражается через предыдущие; отложим все векторы от одной точки коллинеарны

(если не выражается через , то )

, – комланарные

Пусть , – комланарные а)Если среди них есть пара коллинеарных то по п.2 они линейно зависимые. Пара – часть от тройки все линейно зависимые б)Если нет ни одной пары коллинеарных; - не коллинеарные и лежат в плоскости П, отложим от этой же точки все лежат в одной плоскости в силу компланарности )

, - линейно зависимые

4. 1) если есть нулевой – зависимы по п.1 2) если есть коллинеарные – зависимые по п.2 3) если есть компланарные – зависимые по п.3 4) нет ни одной тройки компланарных. отложим от одной точки О , , По предыдущей теореме п.1

Так как нет ни одной тройки компланарных линейно зависимые

Следствия:

1. Один вектор линейно независим он ненулевой

2. Два вектора линейно независимы они неколлинеарны

3. Три вектора линейно независимы они некомпланарны