08_Квантовая_механика_рус.Rtf
$$$001
Примеры центрально-симметричных потенциалов:
A) ангармонический осцилляторный
B) центробежный
C)
двумерный осцилляторный
D)
двумерный осцилляторный
E) кулоновский
F)
линейный типа
G) трехмерный гармонический
H)
– дельта-образный
{Правильный ответ} = B, E, G
{Сложность} = 1
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} = 4
{Семестр} = 7
$$$002
В
центрально-симметричном поле
интегралами движения являются:
A)
оператор импульса
B) оператор проекции импульса на ось z
C)
квадрат углового момента
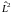и все его проекции
D) квадрат углового момента и любая его проекция
E)
квадрат оператора импульса
и любая его проекция
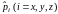
F)
операторы
или
,
или
G)
операторы
,
и все проекции
H) оператор четности
{Правильный ответ} = D, F, H
{Сложность} = 1
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} = 4
{Семестр} = 7
$$$003
Решение
уравнения Шредингера с центральным
потенциалом в приближении факторизации
,
где
– радиальная
волновая функция и
– угловая
сферическая
функция. Совокупность квантовых чисел:
– радиальное,
– орбитальное и магнитное
принимает значения:
A)
=0,
1, 2, …;
=
0, 1, 2, …;
всего
при данном
B) , , m – целые и полуцелые положительные
C)
=0,
1, 2, …;
=
0, 1, 2, …;
через 1
D) , , m – целые и полуцелые, знакопеременные
E)
,
– целые, положительные;
F)
;
;
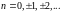G)
=0,
1, 2, …;
=
0, 1, 2, …;
всего
при данном
H)
=
1, 2, …;
=
1, 2, …;
всего
при данном
{Правильный ответ} = A, C, E
{Сложность} = 1
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} = 4
{Семестр} = 7
$$$004
Сферические
функции
образуют ортонормированный вырожденный
базис и являются собственными функциями
операторов
и
:
A)
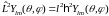
B)
C)
D)
E)
F)
G)
H)
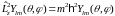
{Правильный ответ} = D, F, H
{Сложность} = 1
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} = 4
{Семестр} = 7
$$$005
Радиальное
уравнение Шредингера для радиальной
функции
для центрально-симметричных полей:
A)
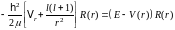
B)
C)
D)
E)
F)
G)
H)
{Правильный ответ} = B, E, G
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} = 4
{Семестр} = 7
$$$006
Условия
на поведение радиальных функций
в нуле связаны с существенной особенностью
центробежного потенциала
:
.
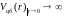Функция
регулярная в нуле и подчиняется
уравнениям:
A)
в интервале
B)
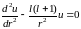в интервале
C)
в интервале
D)
,
при
E)
,
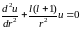при
F)
,
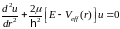где
G)
,
где
H)
,
где
{Правильный ответ} = A, D, H
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} = 4
{Семестр} = 7
$$$007
Энергетические
уровни изотропного гармонического
осциллятора вырождены. Главное квантовое
число в случае декартовых переменных
.
Кратность вырождения уровней
:
A)
1-ое возбужденное состояние
B)
2-ое возбужденное состояние
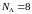
C)
3-е возбужденное состояние
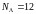
D)
1-ое возбужденное состояние
E) 2-ое возбужденное состояние
F)
3-е возбужденное состояние
G) основное состояние
H)
основное состояние
{Правильный ответ} = D, E, F
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} = 4
{Семестр} = 7
$$$008
В
трехмерном гармоническом осцилляторе
каждому энергетическому уровню
ставится в соответствие значение
главного квантового числа
,
которое является комбинацией радиального
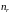и орбитального
квантовых чисел, спектроскопическое
состояние
и кратность вырождения
:
A)
,
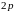
B)
,
C)
D) ,
E)
,
F)
G)
,
H) ,
{Правильный ответ} = C, E, H
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} = 4
{Семестр} = 7
$$$009
Квантовый
ротатор описывает движение частицы
массой
,
закрепленной на жесткой невесомой нити
на расстоянии
относительно центра О. Энергетический
спектр ротатора:
A) вырожден, кратность вырождения
B) не вырожден
C) вырожден, кратность вырождения больше, чем
D) квантован в единицах, пропорциональных моменту инерции
E) квантован в единицах, обратных моменту инерции
F)
G)
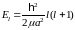
H)
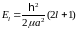
{Правильный ответ} = A, E, G
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} = 4
{Семестр} = 7
$$$0010
Волновые
функции квантового ротатора
должны быть нормированы на единицу.
Явный вид радиальной функции
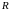определяется соотношением:
A)
B)
C)
D)
E)
F)
G)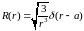
H)
{Правильный ответ} = B, D, G
{Сложность} = 3
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} = 4
{Семестр} = 7
$$$0011
Квантование
энергетического спектра водородоподобных
систем в центрально-симметричном
потенциале
:
A)
B)
C)
D)
,
где
– атомная единица длины
E)
,
где
– атомная единица длины
F)
G)
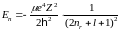
H)
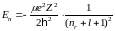
{Правильный ответ} = C, E, F
{Сложность} = 3
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} = 4
{Семестр} = 7
$$$0012
Особенности
движения частицы в поле сферической
симметрии в случае дискретных состояний,
описываемых функцией
:
A) минимальное вырождение
B)
минимальное вырождение
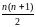
C)
минимальное вырождение
D) решения факторизуются только при переходе к декартовым координатам
E)
решения факторизованы по переменным
и
F)
четность состояний определяется
G)
четность состояний определяется
H)
четность состояний определяется
{Правильный ответ} = A, E, H
{Сложность} = 3
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} = 4
{Семестр} = 7