3. Модифицированные элементы итоговой симплекс-таблицы (при увеличении на 5 кг ресурса s3).
Таблица примет вид.
Базисные переменные |
переменные |
Правая часть |
Правая часть, модифицированные |
||||
|
|
|
|
|
|
|
|
|
1 |
0 |
1/3 |
0 |
0*5 |
9 |
9+0=9 |
|
0 |
0 |
2/3 |
1 |
-2*5 |
8 |
8-10=-2 |
|
0 |
1 |
-1/3 |
0 |
1*5 |
11 |
11+5=16 |
Целевая функция |
0 |
0 |
1/3 |
0 |
1*5 |
29 |
29+5=34 |
При этом
остался прежним,
возросло до
,
целевая функция возросла до
.
Г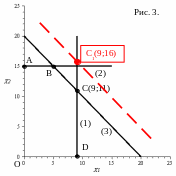
еометрически
это означает следующее.
означает третье ограничение, прямая (3) на рис. 1. Уравнение третьего ограничения имеет вид:
При увеличении ресурса на 5 кг это ограничение примет вид:
Новая точка будет лежать на пересечении прямых (31) и (1). Решим систему
Откуда
,
соответственно
.
Все эти данные отражены в симплекс таблице.
4. Для определения
максимального дополнительного количества
ресурса
,
которое используется полностью и не
приводит к созданию излишка ресурса,
умножим значения столбца
на такой множитель
,
чтобы в правой части модифицированной
таблице ресурс
равнялся нулю:
Отсюда
.
Базисные переменные |
переменные |
Правая часть |
Правая часть, модифицированные |
||||
|
|
|
|
|
|
|
|
|
1 |
0 |
1/3 |
0 |
0*r |
9 |
9+0=9 |
|
0 |
0 |
2/3 |
1 |
-2*r |
8 |
8-2*r=0 |
|
0 |
1 |
-1/3 |
0 |
1*r |
11 |
11+4=15 |
Целевая функция |
0 |
0 |
1/3 |
0 |
1*r |
29 |
29+4=33 |
Базисные переменные |
переменные |
Правая часть |
Правая часть, модифицированные |
||||
|
|
|
|
|
|
|
|
|
1 |
0 |
1/3 |
0 |
0* |
9 |
9+0=9 |
|
0 |
0 |
2/3 |
1 |
-2*4 |
8 |
8-2*4=0 |
|
0 |
1 |
-1/3 |
0 |
1*4 |
11 |
11+4=15 |
Целевая функция |
0 |
0 |
1/3 |
0 |
1*4 |
29 |
29+4=33 |
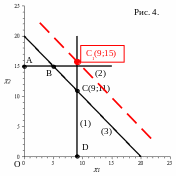
При этом ограничение (3) будет иметь вид:
Геометрически это означает следующее.
Уравнение третьего ограничения стало иметь вид:
Новая точка
будет лежать на пересечении этой прямой
и прямой (1). То есть для нахождения
координат точки
надо решить систему:
Откуда
,
соотвественно:
Все эти данные отражены в симплекс таблице.
5. Модифицированные элементы итоговой симплекс-таблицы (при уменьшении на 2 кг ресурса ).
Базисные переменные |
переменные |
Правая часть |
Правая часть, модифицированные |
||||
|
|
|
|
|
|
|
|
|
1 |
0 |
1/3*2 |
0 |
0 |
9 |
9-2/3= |
|
0 |
0 |
2/3*2 |
1 |
-2 |
8 |
8-4/3= |
|
0 |
1 |
-1/3*2 |
0 |
1 |
11 |
11+2/3= |
Целевая функция |
0 |
0 |
1/3*2 |
0 |
1 |
29 |
29-2/3= |
