4. Решение задачи линейного программирования симплексным методом.

Предположим, что нам надо решить задачу линейного программирования:

(1)

(2)

(3)

симплекс-методом. При этом найти оптимальный производственный план и максимальную прибыль, определить свободный запас каждого ресурса.

Решим ее теперь симплекс методом.

Для этого приведем систему ограничений к каноническому виду, вводя дополнительные переменные - как показано ниже:

То есть система уравнений примет вид:

При этом, чтобы целевая функция не изменилась, коэффициенты перед дополнительными переменными полагаем равными нулю:

Т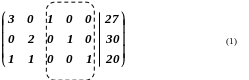 о есть, полагаем, что цены . Таким образом, расширенная матрица системы ограничений примет вид:

Пунктирным прямоугольником выделена единичная матрица, которую мы добавили. Эта единичная матрица дает начальное базисное решение (для чего она и вводится):

Заполняем нулевую симплекс-таблицу. Здесь А₁, А₂, А₃, А₄, А₅, В - столбцы исходной матрицы (1).

Номер симплекс- таблицы	Базис	f	2	1	0	0	0	План В	Q
			А1	А2	А3	А4	А5
0	А3		3	0	1	0	0	27	9
	А4		0	2	0	1	0	30	∞
	А5		1	1	0	0	1	20	20
			-2	-1	0	0	0	0

В последнюю строчку записывают коэффициенты - цены, взятые с обратным знаком.

Чтобы план был оптимальным, необходимо чтобы в последней строке не было неположительных элементов.

Поэтому преобразовывают симплекс-таблицу по определенным правилам так, чтобы в последней строке не осталось неположительных элементов. (За один шаг, или за одну итерацию, обычно это сделать не удается, поэтому проводят несколько итераций по одним и тем же правилам.)

Процесс итерации включает несколько шагов.

1. Определяют ведущий, опорный столбец. При этом ориентируются на последнюю строку, которую мы только что заполняли. А именно, выбирают тот столбец, для которого элемент последней строки имеет наименьшее значение. В нашем случае это элемент , следовательно, ведущий - столбец А₁.

2. В ведущем столбце выбирают ведущий элемент по следующему правилу. Ищут отношение элементов столбца В к соответствующим элементам ведущего столбца А₁:

. Эти значения заносят в последний столбец под названием Q и из них выбирают наименьший элемент. В нашем случае это . То есть ведущий элемент находится на пересечении столбца А₁ и строки А₃.

Теперь все готово для заполнения первой симплекс-таблицы.

3. В ведущей строке делают так, чтобы ведущий элемент (в нашем случае ) стал равным единице. Для этого все элементы ведущей строки делят на ведущий элемент, в нашем случае . Результаты заносят в эту же строку первой таблицы.

4. Далее стремятся к тому, чтобы в остальных строках элементы столбца А₁ стали равными нулю.

В нашем случае во второй строке А₄ на позиции

Номер симплекс- таблицы	Базис	2	1	0	0	0	План В	Q
		А1	А2	А3	А4	А5
0	А3	3	0	1	0	0	27	9
	А4	0	2	0	1	0	30	∞
	А5	1	1	0	0	1	20	20
		-2	-1	0	0	0	0
1		1	0	1/3	0	0	9	∞
	А4	0	2	0	1	0	30	15
	А5	0	1	-1/3	0	1	11	11
		0	-1	2/3	0	0	18

столбца А₁ уже стоит , поэтому с ней мы ничего делать не будем, а просто перепишем.

В третьей строке А₅ в столбце А₁ стоит . Очевидно, чтобы превратить его в ноль, от него нужно отнять . Но прибавлять и отнимать что либо произвольно мы не можем. Мы можем прибавлять и отнимать только соответствующие элементы ведущей строки, умноженные на некоторый, необходимый нам, коэффициент. Поэтому от всех элементов третьей строки мы отнимем соответствующие элементы ведущей строки, деленные на .

Первый элемент ведущей строки , делим его на , получаем , отнимаем от (элемент столбца А₁ третьей строки), получаем и записываем его на место элемента столбца А₁ третьей строки. Дальше аналогично для всех других элементов.

Последний элемент ведущей строки , делим его на , получаем , отнимаем от (последний элемент третьей строки), получаем , и записываем на место последнего элемента третьей строки первой симплекс таблицы.

Дальше последняя строка. В столбце А₁ последней строки стоит . Нам нужно, чтобы вместо стоял бы . Для этого нужно к прибавить . Поэтому мы все элементы ведущей строки умножаем на и прибавляем к соответствующим элементам четвертой строки.

5. Теперь смотрим, что же стало с базисом в результате всех проведенных преобразований. В базисе у нас должны стоять столбцы, для которых элементы в последней строке равнялись нулю. В нулевой симплекс-таблице в последней строке нули стояли в столбцах А₃, А₄ и А₅. Именно поэтому они стояли как базисные. В первой симплекс таблице в последней строке у столбцов А₄ и А₅ нули остались, поэтому они остаются в базисе на своих местах.

Но у элемента А₃ в последней строке стоит уже не ноль, а . Поэтому он уже не может быть базисным. В то же время у столбца А₁ в последней строке появился ноль. Следовательно, теперь этот столбец становится базисным на месте А₃. Но другое название у этого столбца , поэтому мы и запишем там, где раньше стояло А₃.

Следовательно, мы получили первое базисное приближение:

Но это решение еще не является оптимальным, поскольку в последней строчке первой симплекс-таблицы есть еще неположительные элементы.

Поэтому первую симплекс-таблицу преобразовывают дальше, по тем же правилам, стремясь все также к тому, чтобы в последней строке не было неположительных элементов.

1. Определяем ведущий столбец, т.е. столбец с наименьшим значением элемента в последней строке. У нас это будет столбец А₂ со значением элемента .

2. Теперь выбираем ведущий элемент в ведущем столбце А₁, для чего ищем значения Q (как и в нулевой таблице). Заполняем столбец Q. Получили значения - . Выбираем наименьшее, т.е. . Таким образом, ведущий элемент .

3. Мы видим, что третья, ведущая строка остается без изменений, поскольку ведущий элемент уже равен единице. Без изменений остается и первая строка, поскольку в ней элемент А₂ уже равен нулю. Поэтому эти строки также переписываем без изменений.

4. Чтобы во второй строке элемент на А₂ стал равным нулю, все элементы третьей строки умножим на и прибавим к соответствующим элементам второй строки.

Номер симплекс- таблицы	Базис	2	1	0	0	0	План В	Q
		А1	А2	А3	А4	А5
0	А3	3	0	1	0	0	27	9
	А4	0	2	0	1	0	30	∞
	А5	1	1	0	0	1	20	20
		-2	-1	0	0	0	0
1		1	0	1/3	0	0	9	∞
	А4	0	2	0	1	0	30	15
	А5	0	1	-1/3	0	1	11	11
		0	-1	2/3	0	0	18
2		1	0	1/3	0	0	9
	А4	0	0	2/3	1	-2	8
		0	1	-1/3	0	1	11
		0	0	1/3	0	1	29

Чтобы элемент А₂ последней строки стал равным нулю, ко всем элементам последней строки добавим соответствующие элементы третьей, ведущей строки.

5. Теперь последняя строчка. У бывшего базиса в последней строчке стоит ноль, поэтому он остался на своем месте. У бывшего базиса А₄ в последней строчке стоит ноль, поэтому он также остался на своем месте. У бывшего базиса А₅ в последней строчке стоит единица, поэтому он выбывает из базиса. Но теперь в последней строчке ноль стоит у базиса А₂. Поэтому он входит в базис, вместо А₅. Но базис А₂ это , поэтому вместо А₅ запишем .

Во второй симплекс-таблице в последней строчке нет неположительных значений, поэтому полученный план является оптимальным. Итак

Для уяснения экономического смысла перепишем отдельно итоговую симплекс-таблицу.

Базисные переменные	переменные					Правая часть	комментарий
	1	0	1/3	0	0	9	Значение
(А4)	0	0	2/3	1	-2	8	Значение ресурса
	0	1	-1/3	0	1	11	Значение
Целевая функция	0	0	1/3	0	1	29	Максимальное значение прибыли

1. Мы видим, что ресурсы и расходуются полностью и являются дефицитными (их нет в столбце ).

2. Также видно, что остаток ресурса - .

3. Теневая цена для ограничения (1) – первая строка - составляет . То есть, если реализуется 1кг ресурса для первого ограничения сверх нормы, то прибыль возрастет на 1/3 у.е. Необходимо иметь ввиду однако, что так называемая теневая цена никакого отношения к рыночной цене не имеет. Это своя «ценность» внутри данной фирмы.

4. Теневая цена для ограничения (3) – третья строка - составляет . То есть, если реализуется 1кг ресурса третьего ограничения сверх нормы, то прибыль уменьшится на 1/3 у.е.