
- •1.2 Задача про мінімум квадратичного функціоналу. Існування розв’язку задачі про мінімум функціоналу.
- •Задача , ; (1) , ; (2) , , , (3) є:
- •У варіаційному формуванні крайової задачі, як задачі мінімізації квадратичного функціонала, природні граничні умови та диференціальне рівняння становлять
- •Задача для рівняння , ; є:
- •Для задачі, яка має природну граничну умову функціонал енергії:
- •4.3. Енергетичні теореми проблеми власних чисел.
1.2 Задача про мінімум квадратичного функціоналу. Існування розв’язку задачі про мінімум функціоналу.
Яку функцію називають узагальненим розв’язком рівняння Au=f ?
-50% Яка надає максимум функціоналу енергії на множині функцій з простору Ha
100% Яка надає мінімум функціоналу енергії на множині функцій з простору Ha
-50% З якої випливає обмеженість функціоналу на множині функцій простору Ha
Якщо А – додатний оператор, тоді чи має розвязок задача Au=f ?
100% Має і він єдиний
-50% Не має розвязку
-50% Має безліч розв’язків
Чи задовольняє скалярний добуток (u,v)A=(Au,v) аксіоми гільбертового простору ?
-50% Так, задовольняє перші дві
100% Так, задовольняє всі
-50% Не задовольняє
Нехай А-додатний оператор і задача Au=f має розвязок, то якому функціоналу він надає мінімум?
-50% F(u)=(Au,u)
100% F(u)=(Au,u)-2(u,f)
-50% F(u)=2(u,f)
Який скалярний добуток задовольняє всі аксіоми гільбертового простору?
-50% (u,v)A=(u,v)+(v,u)
100% (u,v)A=(Au,v)
-50% (u,v)A=(Au,v)+(u,Av)
Яка норма відповідає енергетичному скалярному добутку (u,v)A=(Au,v) ?
-50% ||u+v||A=(u,v)A1/2
100% ||u||A=(u,u)A1/2
-50% ||u-v||A=-(u,u)A1/2
Якщо А – додатний оператор, тоді чи має розвязок варіаційна задача
F(u)=(u,u)A-2(u,f)?
100% Має u0 є HA і він єдиний
-50% Не має розвязку
-50% Має безліч розв’язків ui є HA
Якщо простір НА - сепарабельний, то чи можна в ньому знайти систему функцій (якщо можна - яку)?
100% ортонормовану
-50% ортогональну
-50% не можна знайти
У якому просторі можна знайти ортонормовану систему функцій {fn}?
100% У сепарабельному просторі НА
-50% У гільбертовому просторі Н
-50% У банаховому просторі B
Якщо послідновність {fn} збіжна за енергетичною нормою скалярного добутку (u,v)A=(Au,v) то за чим вона ще збіжна ?
-50% за нормою бананового простору Р
100% за нормою вихідного простору Н
-50% за нормою сепарабельного простору НА
Який вигляд має повний простір НА?
-50% НА =DA
100% НА =DA доповнений ГА
-50% НА =DА без ГА
Яка нерівність виконується для довільного u є НА, де НА –енергетичний простір?
-50% ||u||A>γ||u||
100% ||u||A>=γ||u||
-50% ||u||A=γ||u||
2.3. Ермітові одновимірні апроксимації на скінченних елементах.
Використовуючи ермітові функції, за вузлові параметри обираєм значення:
50%Функції
-100%Другої похідної функції
50%Першої похідної функції
-100%Всі перелічені варіанти
Вищий порядок гладкості мають базисні функції:
-100%Кусково-лінійні
-100%Лагранжевого типу
100%Ерміта
Дані вузлові параметри використовують для полінома Ерміта
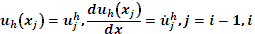
-100%Першого степеня
-100%Другого степеня
100%Третього степеня
Базисні функції ермітового типу є неперервними:
100%Разом з похідними першого порядку
-100%Разом з похідними другого порядку
-100%Нічого з переліченого
На рисунку зображена

100%Ермітова базисна функція першого типу
-100%Кусково-поліноміальна апроксимуюча функція
-100%Ермітова базисна функція другого типу
На рисунку зображена

-100%Ермітова базисна функція першого типу
-100%Кусково-поліноміальна базисна функція
100%Ермітова базисна функція другого типу
Нехай задано два скінченні елементи прямокутної форми, що мають спільну сторону вздовж лінії
 .
На елементах побудовані
апроксимаційні формули ермітового
типу. Чи є функції
.
На елементах побудовані
апроксимаційні формули ермітового
типу. Чи є функції  неперервними в разі
переходу через спільну границю елементів:
неперервними в разі
переходу через спільну границю елементів:
-100%Так, лише функція
100%Так, функція і похідні до першого порядку
-100%Ні, лише похідні першого порядку
-100%Жоден із перекислених варіантів
Для побудови кубічних Ермітових одновимірних апроксимацій на скінченних елементах вигляду
 за
вузлові параметри необхідно
вибрати:
1)
2)
3)
за
вузлові параметри необхідно
вибрати:
1)
2)
3)
-100%Лише 1
-100%Лише 3
100%Лише 2
-100%Жодного із перелічених варіантів
Базисні функції бікубічних апроксимацій ермітового типу на прямокутному скінченному елементі можна поширити на всю область. При цьому розширенні в разі переходу через спільні сторони прямокутників зберігається:
-100%Розривність
100%Неперервність до перших похідних включно
-100%Неперервність до других похідних включно
-100%Лише неперервність функції
У виразі для апроксимації функції
 де
де  і
і  перша компонента в
перша компонента в  відповідає
відповідає
100%Значенню функції в і-1 вузлі
-100%Значенню похідної в і-1 вузлі
-100%Значенню комбінації функції і її похідної в і-1 вузлі
У виразі для апроксимації функції де і друга компонента в відповідає
-100%Значенню функції в і-1 вузлі
100%Значенню похідної в і-1 вузлі
-100%Значенню комбінації функції і її похідної в і-1 вузлі
У виразі для апроксимації функції де і третя компонента в відповідає
100%Значенню функції в і вузлі
-100%Значенню похідної в і вузлі
-100%Значенню комбінації функції і її похідної в і-1 вузлі
-100%Значенню комбінації функції і її похідної в і-тому вузлі
У виразі для апроксимації функції де
 і
і  перша компонента в
обчислюється за формулою:
1)
2)
3)
де
перша компонента в
обчислюється за формулою:
1)
2)
3)
де
 i
i 
100%1
-100%2
-100%3
-100%Жодної правильної відповіді
У виразі для апроксимації функції де і друга компонента в обчислюється за формулою: 1) 2) 3) де i
100%1
-100%2
-100%3
-100%Жодної правильної відповіді
У виразі для апроксимації функції де і третя компонента в обчислюється за формулою: 1) 2) 3) де i
-100%1
-100%2
100%3
-100%Жодної правильної відповіді
Для бікубічної апроксимації ермітового типу у кожній вузловій точці маємо:
-100%Один вузловий параметр
-100%Два вузлових параметри
-100%Три вузлових параметри
100%Чотири вузлових параметри
-100%Жодного вузлового параметра
Ермітова базисна функція має вигляд: 1) 2)
-100% Лише перший варіант
100% Обидва варіанти
-100% Лише другий варіант
-100%Жоден з перечислених варіантів
3.7. Крайові задачі для р-ня Пуассона.
Другою крайовою умовою для рівняння Пуассона є :
-100%Задача Діріхле
100%Задача Неймана
-100%Задача Ньютона
Задача Неймана при (k = 2) для рівняння Пуассона має
100%не має єдиного розв’язку
-100%єдиний розв’язок
-100%має безліч розв’язків
Для того щоб дослідити додатну визначеність операторів головних крайових задач для неоднорідного рівняння Лапласа використовуємо :
-100%нерівність Коші
100%нерівності Фрідріхса і Пуанкаре
-100%нерівність Чебишева
У другій крайовій умові (задача Неймана) для рівняння Пуассона du(x)/dv=0, xϵГ де, (мал. 14.4.1)
-100%a)
100%b)
Крайова задача Неймана для рівняння Пуассона має вигляд : (мал. 14.5.1)
100%a)
-100%b)
-100%c)
Крайова задача Діріхле для рівняння Пуассона має вигляд : (мал. 14.6.1)
-100%a)
100%b)
-100%c)
Крайова задача Ньютона для рівняння Пуассона має вигляд : (мал. 14.7.1)
-100%a)
-100%b)
100%c)
Для крайової задачі Неймана множина області визначення оператора Ak набуде вигляду : (мал. 14.8.1)
-100%a)
100%b)
-100%c)
Для крайової задачі Діріхле множина області визначення оператора Ak набуде вигляду : (мал. 14.9.1)
100%a)
-100%b)
-100%c)
Для крайової задачі Ньютона множина області визначення оператора Ak набуде вигляду : (мал. 14.10.1)
-100%a)
-100%b)
100%c)
Нерівність Фрідріхса має вигляд (мал. 14.11.1)
-100%a)
100%b)
-100%c)
Нерівність Фрідріхса має вигляд (мал. 14.12.1)
-100%a)
100%b)
-100%c)
Оператори трьох головних крайових задач для неоднорідного рівняння Лапласа є додатно визначеними :
-100%ні
100%так
Задачу Ньютона можна сформувати як варіаційну задачу вигряду : (мал.14.14.1)
-100%a)
100%b)
Задачу Неймана можна сформувати як варіаційну задачу вигряду : (мал. 14.15.1)
-100%a)
100%b)
Функцію u у варіаційному вигляді задачі Ньютона належить простору : (мал. 14.16.1)
-100%a)
100%b)
-100%c)
Функцію u у варіаційному вигляді задачі Неймана належить простору : (мал. 14.17.1)
100%a)
-100%b)
-100%c)
Функцію u у варіаційному вигляді задачі Діріхле належить простору : (мал. 14.18.1)
-100%a)
-100%b)
100%c)
В неоднорідному рівнянні Лапласа (мал. 14.19.1): (мал. 14.19.2)
100%a)
-100%b)
-100%c)
Це нерівність (14.20.1)
100%Фрідріхса
-100%Пуанкаре
4.2 Властивості спектра оператора.
Який вигляд має задача на власні значення?
100% Au-λu=0
-50% Au-u=Bu
-50% Au= λu+с
У якому просторі діє оператор А задачі на власні значення вигляду:
Au-λu=0?
100% У гільбертовому просторі Н=L2
-50% У сепарабельному просторі Н
-50% У банаховому просторі B
Що таке спектр оператора ?
100% сукупність власних чисел і власних значень оператора
-50% Власні числа оператора
-50% Власні значення оператора
Що таке власні значення оператора А?
100% значення λ для яких існує відмінний від тотожного нуля розвязок задачі Au-λu=0
-50% нетривіальні значеня розвязку задачі Au-λu=0
-50% сукупність розв’язків задачі Au-λu=0
Що таке власні функції оператора А?
100% нетривіальні значеня розвязку задачі Au-λu=0, які відповідають власним числам
-50% λ для яких існує відмінний від тотожного нуля розвязок задачі Au-λu=0
-50% сукупність розв’язків задачі Au-λu=0
Якими числами є власні числа задачі Au-λu=0 ?
100% дійсними
-50% комплексними
-50% натуральні
Якими є власні числа додатного оператора ?
100% невідємними
-50% додатними
-50% ненульовими
Якими є власні числа додатно визначеного оператора ?
100% додатними
-50% невідємними
-50% недодатними
Якими є власні функції симетричного оператора, що відповідають різним власним числам ?
100% ортогональні
-50% ортонормовані
-50% ортонормовані і ортогональні
Якими є власні функції додатно визначеного оператора, що відповідають різним власним числам ?
100% ортогональні за енергією
-50% ортонормовані за енергією
-50% ортонормовані і ортогональні за енергією
Що визначає якісні характеристики власних чисел та власних функцій ?
100% властивості симетрії, додатності і додатної визначеності оператора А
-50% ортонормованість оператора А
-50% ортонормованість і ортогональність оператора А
Яка задача є спектральною?
100% Au-λu=0
-50% Au-λu=Bu+c
-50% Au=0.
Для системи звичайних диференціальних рівнянь

 вкажіть правильні крайові
умови: a)
вкажіть правильні крайові
умови: a)
 b)
b)
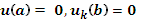 c)
c)

-100%a)
-100%b)
100%c)
Щоб отримати крайову задачу вигляду
 необхідно
в
крайовій задачі
необхідно
в
крайовій задачі
 зробити
таку заміну:
a)
зробити
таку заміну:
a)
 b)
b)

100%a)
-100%b)
-100%Жодна з відповідей не вірна
У гільбертовому просторі
 векторних функцій скалярний добуток
визначається наступним співвідношенням:
a)
векторних функцій скалярний добуток
визначається наступним співвідношенням:
a)
 b)
b)
 c)
c)

100%a)
-100%b)
-100%c)
-100% Жодна з відповідей не вірна
У гільбертовому просторі векторних функцій норма визначається наступним співвідношенням: a)
 b)
b)
 c)
c)

-100%a)
-100%b)
100%c)
Для крайової задачі область визначення оператора
 оператора можна задати
співвідношенням:
a)
оператора можна задати
співвідношенням:
a)
 b)
b)
 c)
c)

-100%a)
100%b)
-100%c)
Маємо крайову задачу

 закінчіть
формулювання леми: Нехай
закінчіть
формулювання леми: Нехай
 – симетричні
матриці, тоді оператор задачі (1), (2) …
– симетричні
матриці, тоді оператор задачі (1), (2) …
100%симетричний
-100%додатний
-100%додатно визначений
Маємо крайову задачу закінчіть формулювання теореми: Нехай
 – додатно
визначена матриця
– додатно
визначена матриця
 а
а
 – невід’ємна
матриця
– невід’ємна
матриця
 Тоді
оператор задачі (1), (2) …
Тоді
оператор задачі (1), (2) …
-100%симетричний
-100%додатний
100%додатно визначений
Якщо оператор задачі
 додатно
визначений. Тоді її можна записати у
такому варіаційному формулюванні:
a)
додатно
визначений. Тоді її можна записати у
такому варіаційному формулюванні:
a)
 b)
b)

100%a)
-100%b)
-100%немає правильної відповіді
Який порядок має система звичайних диференціальних рівнянь:
-100%перший
100%другий
-100%k-тий
-100%(s-1)-ий
Матриця системи лінійних алгебричних рівнянь МСЕ формується з матриць
 де
де  тут є
тут є
100%матриця мас
-100%матриця жорсткості
-100%гранична матриця
-100%немає правильної відповіді
Матриця системи лінійних алгебричних рівнянь МСЕ формується з матриць де
 тут є
тут є
100%матриця жорсткості
-100%матриця мас
-100%гранична матриця
-100%немає правильної відповіді
Матриця жорсткості
 системи рівнянь МСЕ обчислюється
наступним чином: a)
системи рівнянь МСЕ обчислюється
наступним чином: a)
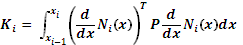 b)
b)
 c)
c)

100%a)
-100%b)
-100%c)
Матриця мас
 системи рівнянь МСЕ обчислюється
наступним чином: a)
системи рівнянь МСЕ обчислюється
наступним чином: a)
 b)
b)
 c)
c)

-100%a)
100%b)
-100%c)
Стовпець правих частин системи рівнянь МСЕ обчислюється наступним чином: a)
 b)
b)
 c)
c)

-100%a)
-100%b)
100%c)
Структура системи лінійних алгебраїчних рівнянь на рисунку зображена:

100%вірно
-100%невірно
Варіаційні формулювання
 або
або  є еквівалентними:
є еквівалентними:
100%так
-100%ні
Апроксимація на скінченних елементах.
Теорема про апроксимацію кусково-лінійними базисними функціями.
Функція з компактним носієм – це функція яка
-100%Відмінна від нуля на всій області визначення
100%Відмінна від нуля в певній частині області визначення
-100%Має область значень [1,2]
МСЕ - це
-100%Метод середніх елементів
100% Метод скінченних елементів
-100%Міжнародний союз економістів
В МСЕ область скінченного елемента позначають через
-100%N
100%

-100%Q
В МСЕ (за означенням Сьярле) через позначають
100% Область скінченного елемента
-100%k – вимірний простір функцій
-100%Набір лінійно незалежних функціоналів
В МСЕ (за означенням Сьярле) через N позначають
-100% Область скінченного елемента
100%k – вимірний простір функцій
-100%Набір лінійно незалежних функціоналів
В МСЕ (за означенням Сьярле) через Q позначають
-100% Область скінченного елемента
-100%k – вимірний простір функцій
100%Набір лінійно незалежних функціоналів
В МСЕ трійку значень
 називають
називають
-100% власними значеннями
100% скінченним елементом
-100% набір лінійно незалежних функцій
Нехай скінченний елемент і нехай
 базис простору
базис простору
 ,
причому
,
причому
 ,
тоді базис
називають
,
тоді базис
називають
-100% власним
100% вузловим
-100% компактним
Матричний запис апроксимуючої функції на скінченному елементі
 має вигляд
має вигляд
-100%

100%

-100%

-100%

Похибка апроксимації кусково-лінійними базисними функціями оцінюється через
50%

50%

-100%

-100%

4.9. Числовий аналіз спектральної задачі Штурма-Ліувіля.
Задача на власні значення для оператора Штурма-Ліувілля має вигляд
100%

-100%

-100%

-100%

Умови накладені на коефіцієнти p(x) та q(x) для задачі
У вигляді
![]() і вважатимемо їх неперервними функціями
забезпечує
і вважатимемо їх неперервними функціями
забезпечує
50% Існування дискретного спектра оператора задачі
50% Нескінченну послідовність дійсних чисел
-100% Не існування спектра оператора задачі
-100% Існування неперервного спектра оператора задачі
Якщо p,q=const то для
власні числа і функції
-100% Не існують
100% Можна знайти у явному вигляді
-100% Набувають лише від’ємних значень
Якщо коефіцієнти оператора Штурма-Ліувілля є сталими то елементи матриць
 і
і
 є
є
100% Сталими числами
-100% Інтегралами
-100% Поліномами
Оцінка похибки задачі на власні значення для оператора Штурма-Ліувілля становить
100%

-100%

-100%

1.9. Абстрактна вар. задача і 1.10. Метод Бубнова-Гальоркіна.
Для побудови наближеного розв’язку варіаційної задачі
 (1)
(1)
-100%
 –
лінійно незалежна система,
–
лінійно незалежна система, 
100% – лінійно незалежна система, – повна система,
-100% – повна система,
 скінченновимірний
підпростір простору
скінченновимірний
підпростір простору  ,
натягнутий на базисні функції
,
натягнутий на базисні функції
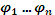 .
Наближений розв’язок
варіаційної задачі, який шукаємо у
м-м Бубнова-Гальоркіна, запишемо у
вигляді
.
Наближений розв’язок
варіаційної задачі, який шукаємо у
м-м Бубнова-Гальоркіна, запишемо у
вигляді
100%

-100%

-100%

Наближений розв’язок варіаційної задачі (1) запишемо
 ,
де
,
де
100%
 – невідомі
коефіцієнти;
– невідомі
коефіцієнти;
-100% – базисні функції;
-100% – наближені розв'язки;
Наближений розв’язок варіаційної задачі (1) запшемо , де
-100%
 – невідомі
коефіцієнти;
– невідомі
коефіцієнти;
100% – базисні функції;
-100% – наближені розв'язки;
Для знаходження невідомих коефіцієнтів наближений розв’язок підставимо у варіаційну задачу
 і
приймемо
і
приймемо  .
Отримаємо СЛАР:
.
Отримаємо СЛАР:
-100%

100%

-100%

Єдиність розв'язку даної СЛАР випливає:
-100%
 з
умов, накладених на базисні функції;
з
умов, накладених на базисні функції;-100% з леми Сеа;
100% з теореми Лакса-Мільграма;
Наближений розв’язок варіаційної задачі (1) шукаємо у Sn, де
100% Sn - повний підпростір простору V;
-100% Sn - простір Соболєва;
-100% правильна відповідь відсутня;
Існування розв'язку в Sn забезпечує
-100% лема Сеа;
-100% теорема про мінімум функціоналу енергії;
100% теорема Лакса-Мільграма;
Для дослідження проблеми збіжності послідовності наближених розв'язків використовують
-100% лему Сеа;
-100% теорема про мінімум функціоналу енергії;
100% теорема Лакса-Мільграма;
Згідно леми Сеа виконується наступна оцінка:
-100%

-100%

100%
 ;
;
В лемі Сеа виконується оцінка
 ,
де
,
де
-100% C > 0;
-100% C не залежить від вимірності простору Sn;
100% всі варіанти правильні;
В лемі Сеа виконується оцінка , де
100% u0 – розв’язок варіаційної задачі;
-100% u0 – наближений розв’язок;
-100% u0 – довільна функція з підпростору Sn;
В лемі Сеа виконується оцінка , де
-100% un – розв’язок варіаційної задачі;
100% un – наближений розв’язок;
-100% un – довільна функція з підпростору Sn;
В лемі Сеа виконується оцінка , де
-100% vn – розв’язок варіаційної задачі;
-100% vn – наближений розв’язок;
100% vn – довільна функція з підпростору Sn;
На підставі леми Сеа доводимо
-100% теорему про збіжність послідовності наближених розв’язків до узагальненого розв’язку;
100% існування розв’язку варіаційної задачі;
-100% всі варіанти правильні;
Теорема про збіжність послідовності наближених розв’язків методу Бубнова-Гальоркіна до узагальненого розв’язку варіаційної задачі, дає таку оцінку:
-100%
100%

-100%

Оцінка
 означає
означає
100% збіжність за нормою послідовності наближених розв'язків варіаційної задачі методу Б-Г до слабкого розв'язку;
100% збіжність за нормою послідовності наближених розв'язків варіаційної задачі методу Б-Г до точного розв'язку;
-100% збіжність послідовності наближених розв'язків варіаційної задачі методу Б-Г ;
Для побудови наближеного розв’язку варіаційної задачі (1)
-100% – лінійно незалежна система,
100% – лінійно незалежна система, – повна система,
-100% – повна система,
скінченновимірний підпростір простору , натягнутий на базисні функції . Наближений розв’язок варіаційної задачі, який шукаємо у м-м Бубнова-Гальоркіна, запишемо у вигляді
100%
-100%
-100%
Наближений розв’язок варіаційної задачі (1) запишемо , де
100% – невідомі коефіцієнти;
-100% – базисні функції;
-100% – наближені розв'язки;
Наближений розв’язок варіаційної задачі (1) запшемо , де
-100% – невідомі коефіцієнти;
100% – базисні функції;
-100% – наближені розв'язки;
Для знаходження невідомих коефіцієнтів наближений розв’язок підставимо у варіаційну задачу і приймемо . Отримаємо СЛАР:
-100%
100%
-100%
Єдиність розв'язку даної СЛАР випливає:
-100% з умов, накладених на базисні функції;
-100% з леми Сеа;
100% з теореми Лакса-Мільграма;
Наближений розв’язок варіаційної задачі (1) шукаємо у Sn, де
100% Sn - повний підпростір простору V;
-100% Sn - простір Соболєва;
-100% правильна відповідь відсутня;
Існування розв'язку в Sn забезпечує
-100% лема Сеа;
-100% теорема про мінімум функціоналу енергії;
100% теорема Лакса-Мільграма;
Для дослідження проблеми збіжності послідовності наближених розв'язків використовують
-100% лему Сеа;
-100% теорема про мінімум функціоналу енергії;
100% теорема Лакса-Мільграма;
Згідно леми Сеа виконується наступна оцінка:
-100%
-100%
100% ;
В лемі Сеа виконується оцінка , де
-100% C > 0;
-100% C не залежить від вимірності простору Sn;
100% всі варіанти правильні;
В лемі Сеа виконується оцінка , де
100% u0 – розв’язок варіаційної задачі;
-100% u0 – наближений розв’язок;
-100% u0 – довільна функція з підпростору Sn;
В лемі Сеа виконується оцінка , де
-100% un – розв’язок варіаційної задачі;
100% un – наближений розв’язок;
-100% un – довільна функція з підпростору Sn;
В лемі Сеа виконується оцінка , де
-100% vn – розв’язок варіаційної задачі;
-100% vn – наближений розв’язок;
100% vn – довільна функція з підпростору Sn;
На підставі леми Сеа доводимо
-100% теорему про збіжність послідовності наближених розв’язків до узагальненого розв’язку;
100% існування розв’язку варіаційної задачі;
-100% всі варіанти правильні;
Теорема про збіжність послідовності наближених розв’язків методу Бубнова-Гальоркіна до узагальненого розв’язку варіаційної задачі, дає таку оцінку:
-100%
100%
-100%
Оцінка означає
100% збіжність за нормою послідовності наближених розв'язків варіаційної задачі методу Б-Г до слабкого розв'язку;
100% збіжність за нормою послідовності наближених розв'язків варіаційної задачі методу Б-Г до точного розв'язку;
-100% збіжність послідовності наближених розв'язків варіаційної задачі методу Б-Г ;
1.8. Слабкий розв’язок крайової задачі і 1.9. Абстрактна варіаційна задача.
Теорему про функціонал енергії можна використовувати для запису варіаційних формулювань задач, оператори яких є
-33.33% від’ємними
100% принаймі додатніми
-33.33% принаймі відємними
-33.33% будь-якими
Безрозмірна стала, число Пекле позначається
-33.33%

100%

-33.33%

-33.33%

Простір Соболєва позначається
-50%

-50%

100%

Простір Соболєва
 визначає
функції які
визначає
функції які
-50%
 які
диференційовані на проміжку
які
диференційовані на проміжку  разом з узагальненими похідними другого
порядку.
разом з узагальненими похідними другого
порядку.-50% які диференційовані на проміжку разом з узагальненими похідними першого порядку.
100% які інтегровані на проміжку разом з узагальненими похідними до другого порядку.
Нехай маємо одновимірний процесс перенесення забруднень
 та граничні умови
та граничні умови  тоді область визначення цієї задачі
можна записати
тоді область визначення цієї задачі
можна записати
-33.33%

100%

-33.33%

-33.33%

Слабким розв'язком задачі
називається
функція ![]() яка
яка
-100% задовольняє варіаційне рівння
 та виконується
та виконується 
100% задовольняє варіаційне рівння
 та виконується
та виконується
Якщо функція є слабким розв’язком задачі тоді
-100%![]() не задовольняє
варіаційне формулювання задачі
не задовольняє
варіаційне формулювання задачі
100%![]() задовольняє
варіаційне формулювання задачі
задовольняє
варіаційне формулювання задачі
Задано варіаційне рівняння
![]()
![]()
тоді загальний вигляд варіаційної задачі матиме вигляд
-100%
 де
де 
100%
 де
де 
Задано варіаційну задачу
![]() де
де ![]()
Питання існування і єдиності слабкого розв’язку цієї варіаційної задачі розглянуто у теоремі
-33.33% про мінімум квадратичного функціонала
100% Лакса - Мільграма
-33.33%

-33.33%

У теоремі Лакса – Мільграма розглядається
-50% простір Соболєва
-50%

100% простір Гільберта
Згідно з теоремою Лакса – Мільграма білінійна норма
-50%

-50%

100%

Згідно з теоремою Лакса – Мільграма білінійна норма
![]()
-50% неперервна
-50%

100% неперервна та V- еліптична
Згідно з теоремою Лакса – Мільграма лінійна норма
![]()
-50% неперервна та

100% неперервна
Згідно з теоремою Лакса – Мільграма лінійна норма
неперервна тобто виконується
-50%

-50%

100%

За теоремою Лакса – Мільграма варіаційна задача
де
де на задані лінійні і білінійні норми задані певні обмеження.
Має єдиний розв’язок і виконується
-50% , α - стала
-50% , α - стала
100% , α - стала
1.8. Слабкий розв’язок крайової задачі і 1.9. Абстрактна варіаційна задача.
Теорему про функціонал енергії можна використовувати для запису варіаційних формулювань задач, оператори яких є
-33.33% від’ємними
100% принаймі додатніми
-33.33% принаймі відємними
-33.33% будь-якими
Безрозмірна стала, число Пекле позначається
-33.33%
100%
-33.33%
-33.33%
Простір Соболєва позначається
-50%
-50%
100%
Простір Соболєва визначає функції які
-50% які диференційовані на проміжку разом з узагальненими похідними другого порядку.
-50% які диференційовані на проміжку разом з узагальненими похідними першого порядку.
100% які інтегровані на проміжку разом з узагальненими похідними до другого порядку.
Нехай маємо одновимірний процесс перенесення забруднень та граничні умови тоді область визначення цієї задачі можна записати
-33.33%
100%
-33.33%
-33.33%
Слабким розв'язком задачі
називається функція яка
-100% задовольняє варіаційне рівння та виконується
100% задовольняє варіаційне рівння та виконується
Якщо функція є слабким розв’язком задачі тоді
-100% не задовольняє варіаційне формулювання задачі
100% задовольняє варіаційне формулювання задачі
Задано варіаційне рівняння
тоді загальний вигляд варіаційної задачі матиме вигляд
-100% де
100% де
Задано варіаційну задачу
де
Питання існування і єдиності слабкого розв’язку цієї варіаційної задачі розглянуто у теоремі
-33.33% про мінімум квадратичного функціонала
100% Лакса - Мільграма
-33.33%
-33.33%
У теоремі Лакса – Мільграма розглядається
-50% простір Соболєва
-50%
100% простір Гільберта
Згідно з теоремою Лакса – Мільграма білінійна норма
-50%
-50%
100%
Згідно з теоремою Лакса – Мільграма білінійна норма
-50% неперервна
-50%
100% неперервна та V- еліптична
Згідно з теоремою Лакса – Мільграма лінійна норма
-50% неперервна та
100% неперервна
Згідно з теоремою Лакса – Мільграма лінійна норма
неперервна тобто виконується
-50%
-50%
100%
За теоремою Лакса – Мільграма варіаційна задача
де
де на задані лінійні і білінійні норми задані певні обмеження.
Має єдиний розв’язок і виконується
-50% , α - стала
-50% , α - стала
100% , α - стала
1.4. Головні та природні граничні умови.
Задача з неоднорідними граничними умовами.
Нехай диференціальне рівняння має порядок 2k. Тоді граничні умови, що містять похідні до порядку k-1 включно є
-100% природними граничними умовами
100% головними граничними умовами
Нехай диференціальне рівняння має порядок 2k. Тоді граничні умови, що містять похідні порядку k та вище є
-100% головними граничними умовами
100% природними граничними умовами
У варіаційному формуванні крайової задачі, як задачі мінімізації квадратичного функціонала, природні граничні умови та диференціальне рівняння становлять
-100% достатні умови мінімуму функціонала
100% необхідні умови мінімуму функціонала
-100% необхідні і достатні умови мінімуму функціонала
Розглянемо мішану крайову задачу для рівняння Пуассона
 ,
,
 ;
(1)
;
(1)
 ,
,
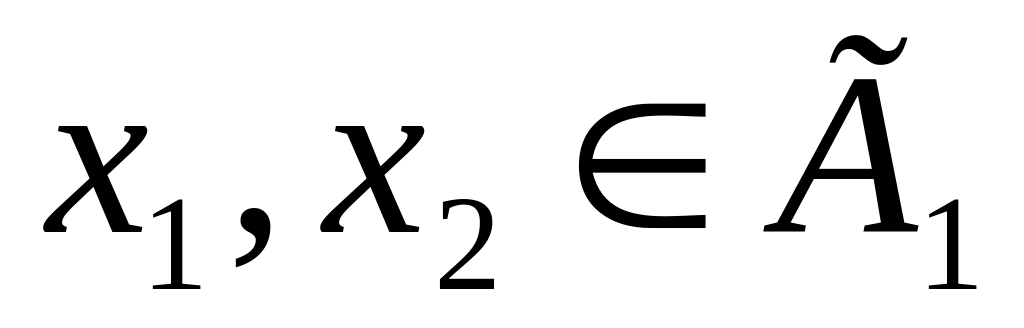 ;
(2)
;
(2)
 ,
,
 ,
,
 ,
(3)
Гранична
умова (2) є:
,
(3)
Гранична
умова (2) є:
100% головною умовою
-100% природною умовою
Розглянемо мішану крайову задачу для рівняння Пуассона
 ,
;
(1)
,
,
;
(1)
,
 ;
(2)
,
,
,
(3)
Гранична умова
(3) є:
;
(2)
,
,
,
(3)
Гранична умова
(3) є:
100% природною умовою
-100% головною умовою
Розглянемо мішану крайову задачу для рівняння Пуассона , ; (1) , ; (2) , , , (3) Ця задача еквівалентна задачі про мінімум функціонала енергії який має вигляд: 1.
 2.
2. 3.
3.
-100% 1
-100% 2
100% 3
7. Розглянемо мішану крайову задачу для рівняння Пуассона , ; (1) , ; (2) , , , (3) Ця задача еквівалентна задачі про мінімум функціонала енергії який має вигляд: (4). Чи вірно, що необхідними умовами функціонала (4) є рівняння (1) і граничні умови (2):
100% ні
-100% так
