Регулирование уровня с помощью каскадной сар. Методика расчета системы.
Системы несвязанного регулирования.
С
труктурная
схема объекта.
W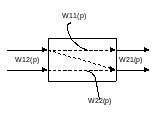
11,
W22
– передаточные функции по основным
каналам W122,
W21-
Передаточные функции по перекрестны
каналам
(2)
При проектировании систем автоматизации таких объектов существует два подхода:
Построение несвязанных м/у собой одноконтурных систем регулирования для каждого из регулируемого параметра.
Введение дополнительных перекрестных связей м/у рег-рами одноконтурных систем с целью компенсации их взаимного влияния.
Структурная схема для расчета регулятора Wрег11(р)
(3)
(4)
…………………….
WВ(P)
WЭ1=Wоб11(p)*[1+Wв(p)*WА2(p)] (5)
(6)
путем аналогичных рассуждений можно получить:
WЭ2=Wоб22(p)*[1+Wв(p)*WА1(p)] (8)
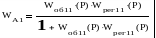(9)
Расчет параметров настройки регуляторов в такой системе осуществляется в 2 этапа:
-на первом этапе рассчитываются параметры настройки регуляторов без учета перекрестных связей на основании выражений (6) и (9)
-на втором этапе передаточные функции эквивалентных объектов рассчитываются по (5) и (6), на основании (6), (9) и вновь считаются параметры настройки.
Наличие перекрестных связей означает ухудшение устойчивости системы.
Пусть связи очень сильны:
Wоб11(P)=Wоб22(P)=Wоб12(P)=Wоб21(P)=Wоб(P) (10)
Wрег11(P)=Wрег22(P)=Wрег(P) (11)
У1(Р)=Wоб(P)*Xв(P)-Wоб(P)*Wрег(P)*У1(Р)-Wоб(P)*Wрег(P)*У2(Р) (12)
У2(Р)=Wоб(P)*Xв(P)-Wоб(P)*Wрег(P)*У1(Р)-Wоб(P)*Wрег(P)*У2(Р) (13)
Принимаем У1=У2
У1(Р)= Wоб(P)*Xв(P)-2Wоб(P)*Wрег(P)*У1(Р)
(14)
Системы автономного регулирования.
Построение таких систем основано на применении двух принципов
-принцип автономности
-принцип инвариантности
Принцип автономного регулирования заключается в достижении независимости двух взаимосвязных через объект регулирования параметров
Система автономного регулирования может быть построена на основе принципа инвариантности.
В нашем случае для получения автономной системы регулирования необходимо добиться инвариантности У2 по отношению Х1 и У1 по отношению Х2
С
этой целью в схему вводятся динамические
компенсаторы, выходные сигналы которых
поступают на соответствующие входы
объекта.
(1)
(2)
Хк12(Р)=Wk12(P)*Xp1(P) (3) Хк21(Р)=Wk21(P)*Xp2(P) (4)
Подставим 3 и 4 в 1
(5)
Для достижения инвариантности У1(Р) по отношению к Хр2 необходимо:
Wоб21(Р)-Wоб11(Р)*Wк21(Р)=0 (6)
(7)Путем
аналогичных рассуждений можно получить:
(8) Выражение 7 и 8 соответствуют выражениям для степеней связи объекта по перекрестным каналам.
Запишем уравнение для регуляторов
Хр1=Wр1(Р)*[(У13(Р)-У2(Р)] (9)
Xp2=Wp2(P)*[У23(Р)-У2(Р)] (10)
Подставим 9 в 5 с учетом 6:
(11)
Путем аналогичных преобразований можно получить:
(12)
Как видно из выражений 11 и 12 расчет параметров настройки регуляторов Р1 и Р2 можно вести независимо друг от друга что соответствует принципу автономности. Однако характеристическое уравнение записано для каждой системы включает передаточные функции компенсаторов, что усложняет расчет регуляторов. На основании опыта расчета подобных систем выбор типа регулирования несвязное или автономное рекомендуется выбирать в соответствии со значением степени взаимосвязи, рассчитываемой при ω=0 и рабочих частотах регуляторов ωр1 и ωр2
(13)
При К≤0,2 можно ограничиться несвязным регулированием. При К≥0,2 рекомендуется в систему включить динамический компенсатор.