4.2 Расчет оптимальных настроек регулятора

Регулятор работает в дискретном режиме, а передаточная функция объекта регулирования непрерывна, поэтому необходимо рассчитать Z-передаточную функцию объекта. Для этого в систему вводится экстраполятор (фиксатор) нулевого порядка с передаточной функцией . Фиксатор нулевого порядка сохраняет измеренную в начале каждого периода квантования амплитуду на весь период квантования. В результате структурная схема САР примет вид, представленный на рисунке 4.2.

Рисунок 4.2 – Структурная схема дискретной САР

Для того чтобы выбрать тип регулятора, определяем отношение τ_об/Т_об:

.

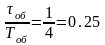Отношение 0,2<_об/T_об<0,7, следовательно, для регулирования будем использовать ПИ-регулятор.

Приведенная непрерывная часть системы представляет собой последовательное включение фиксатора нулевого порядка и объекта с заданной передаточной функцией:

. (4.5)

Z-передаточная функция приведенной части рассчитывается по формуле:

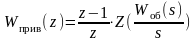. (4.6)

Следовательно, Z-передаточная функция приведенной части примет вид:

Передаточная функция дискретного ПИ-регулятора имеет вид:

. (4.7)

Передаточная функция разомкнутой системы :

Заменяем и получаем комплексную частотную характеристику (КЧХ) или амплитудно-фазовую частотную характеристику разомкнутой системы (АФЧХ):

Так как Т=1, то частоту при построении КЧХ можно изменять в пределах или .

По номограммам Солодовникова при известном значении допустимого перерегулирования определяется , модуль , запас по фазе и [9].

На комплексной плоскости строится окружность:

. (4.8)

Радиус данной окружности определяется по формуле:

. (4.8)

Центр окружности лежит в точке О:

КЧХ строится на том же графике, что и запретная область. При этом задается и подбирается такой , чтобы КЧХ касался запретной области, но не пересекал ее границы. Оптимальными являются те значения, для которых отношение К_р/Т_и является наибольшим. Интервал варьирования будет от 2 до 6, так как наибольшее значение К_р/Т_и приходится на =3.2. Шаг выберем 0.4.

Результаты сводятся в таблицу 4.1.

Таблица 4.1 – Значения настроек ПИ-регулятора

Tи	2	2.4	2.8	3.2	3.6	4	4.4	4.8	5.2	5.6	6
Кр	0.383	0.538	0.702	0.829	0.912	0.968	1.01	1.043	1.07	1.0925	1.113
Кр/Ти	0.1915	0.22417	0.25071	0.25906	0.25333	0.242	0.2295	0.2173	0.20577	0.19509	0.1855

Оптимальные настройки, таким образом, равны , .

Для того чтобы убедиться в оптимальности полученных настроек, нужно рассчитать прямые и косвенные показатели качества:

Косвенные показатели качества определяются по АЧХ замкнутой системы (рисунок 4.3).

Рисунок 4.3 – Амплитудно – частотная характеристика замкнутой системы при настройках ПИ-регулятора К_{р опт} = 0.829 , Т_{и опт} =3.2

Фактическое значение частотного показателя колебательности , то есть расчет можно считать удовлетворительным.

Прямые показатели качества определяются по переходной характеристике замкнутой системы (рисунок 4.4).

Рисунок 4.4 – График переходной характеристики замкнутой системы при настройках ПИ-регулятора К_{р опт} = 0.829, Т_{и опт} =3.2

Прямые показатели качества:

перерегулирование σ_факт =12.3% < σ_доп =20%;

время регулирования t_p=9с < t_доп=(3÷4)Т_об=12 с ÷ 16 с.

Так как полученные показатели качества управления меньше допустимых, настройки ПИ-регулятора можно считать оптимальными.