4. Проверка статистических гипотез

Установление закономерностей, которым подчинены случайные явления, основано на изучении статистических данных - результатах наблюдений.

Задачи математической статистики следующие:

1) указать способы сбора и группировки статистических сведений;

2) разработать методы анализа статистических данных, в зависимости от целей исследования.

Пусть требуется изучить совокупность однородных объектов относительно некоторого количественного признака, например, относительно размера детали. Предполагаем, что деталей много и сплошное обследование стоит слишком дорого. Необходимо решить: как путём обследования ограниченного количества деталей сделать вывод о размерном параметре всей совокупности.

Выборочной совокупностью (выборкой) называют совокупность случайно отобранных объектов. Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

Выборка должна быть репрезентативной, т.е. хорошо представлять генеральную совокупность. В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если её осуществить случайно, т.е. каждый объект из генеральной совокупности достаточно большого объёма (количество объектов в указанной совокупности) отбирается случайно.

Генеральной средней называют среднее арифметическое значений рассматриваемого признака Х генеральной совокупности. Если рассматривать обследуемый признак Х генеральной совокупности как случайную величину, то генеральная средняя будет равна математическому ожиданию признака, т.е. =М(Х).

Выборочной средней называют среднее арифметическое признака выборочной совокупности. Выборочная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам , т.е.

.

Дисперсия равна среднему квадратов значений признака минус квадрат общей средней, а именно:

.

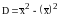Эта формула записана на основании теоремы, в которой доказывается, что , где - общая средняя.

Рассмотрение эмпирического ряда как выборки из генеральной совокупности является основой статистических выводов. В этом смысле эмпирические ряды (см., например, табл. 2.2 для 160-ти измерений предела текучести алюминиевых прутков) являются выборками.

Доверительный интервал. Часто возникает проблема, как на основе ограниченного числа наблюдений (измерений) сделать вывод о величине числовых характеристик генеральной совокупности (математическое ожидание, среднеквадратическое отклонение и т.д.). Так как выборочные наблюдения носят случайный характер, то вычисленные по ним статистические характеристики также колеблются от выборки к выборке. Поэтому для каждой статистической характеристики, вычисленной по данным выборки, следует определить точность оценки. Эта точность содержится в доверительном интервале.

Пусть имеется нормально распределённая генеральная совокупность с математическим ожиданием М и средним квадратичным отклонением . По результатам отобранной из этой совокупности выборки объёмом n вычислена средняя арифметическая . Относительно разности М- можно с вероятность, например, 95% утверждать, что она находится в интервале или

Если вместо доверительной вероятности S=95% желательна, например, вероятность S=99%, то коэффициент 1,96 следует заменить на 2,58.

Дисперсия определяется как средний квадрат отклонения отдельных значений от математического ожидания. Для выборки объёма n имеем:

Так как обычно математическое ожидание неизвестно, то вместо приведенной формулы используют соотношение:

где - частота значений .

Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определённый вид, например R, выдвигают гипотезу о законе распределения R. Задача состоит в том, как подтвердить или опровергнуть выдвинутую статистическую гипотезу.

Возможны статистические гипотезы: о равенстве параметров двух или нескольких распределений, о независимости выборок. Для проверки статистических гипотез используют различные критерии. Заметим, что все критерии не доказываю справедливость той или иной статистической гипотезы, а лишь устанавливают, на принятом уровне значимости, её согласие или несогласие с данными наблюдений.

Для оценки степени близости эмпирического распределения теоретическому существуют специально подобранные случайные величины - критерии согласия Пирсона, Колмогорова, Смирнова и др. Проверка гипотезы о нормальном распределении генеральной совокупности чаще всего осуществляется при помощи критерия согласия Пирсона ( -критерий).

Определение сходимости эмпирического и теоретического распределений с помощью критерия согласия производится следующим образом. Разбиваем всю область изменения случайной величины на m интервалов и подсчитываем количество событий . Затем сравниваем эмпирические и теоретические частоты, которые обычно несколько различаются.

Случайно ли расхождение частот? Возможно, что расхождение случайно (незначимо) и объясняется малым числом наблюдений, либо способом их группировки и другими причинами. Возможно, что расхождение частот не случайно (значимо) и объясняется тем, что теоретические частоты вычислены, исходя из неверной гипотезы о нормальном распределении генеральной совокупности. Критерий Пирсона отвечает на поставленный выше вопрос.

Итак, для некоторого эмпирического распределения принимаем нулевую гипотезу: генеральная совокупность распределена нормально. Для проверки гипотезы вычисляем критерий Пирсона:

,

где - число сравниваемых частот; , - эмпирические и теоретические частоты i-го интервала случайной величины.

Очевидно, что чем меньше различаются теоретические и эмпирические частоты, тем меньше величина критерия и, следовательно, он характеризует близость сравниваемых распределений.

Алгоритм вычисления теоретических частот нормального распределения. следующий:

1. Интервал наблюдаемых значений Х (выборки объёма ) делим на интервалов одинаковой длины. Находим середины каждого интервала и частоту попадания признака в i-ый интервал.

2. Вычисляем выборочные .

3. Нормируем случайную величину Х, переходя к

и вычисляем концы интервалов .

Здесь наименьшее значение Z= , а наибольшее .

4. C использованием функции Лапласа Ф(z) (табл.1, Приложение) вычисляем теоретические вероятности = попадания Х в интервалы .

5. Находим искомые теоретические частоты .

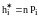6. Вычисляем количество степеней свободы по формуле: ,

где - число параметров теоретического распределения.

7. Задаёмся малой вероятностью - уровнем значимости . Затем ищем критическую точку исходя из требования, чтобы, при условии справедливости нулевой гипотезы (генеральная совокупность распределена нормально), вероятность того, что рассчитанный критерий примет значение, больше , была равна принятому достаточно малому уровню значимости:

.

8. Определяем значение и .

9. По табл.1 Приложения определяем критическое значение .

10. Если < , то делаем вывод: между рассматриваемыми эмпирическим и теоретическим распределением нет существенной разницы.

Необходимым условием применения критерия является наличие в каждом из интервалов по меньшей мере 5-10 наблюдений.