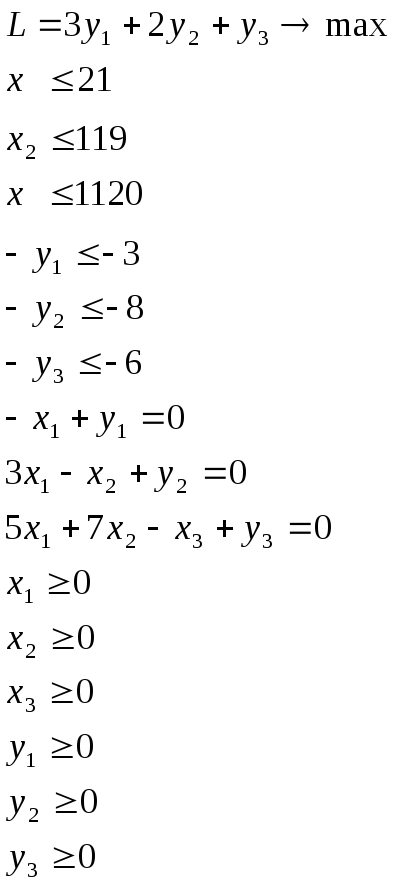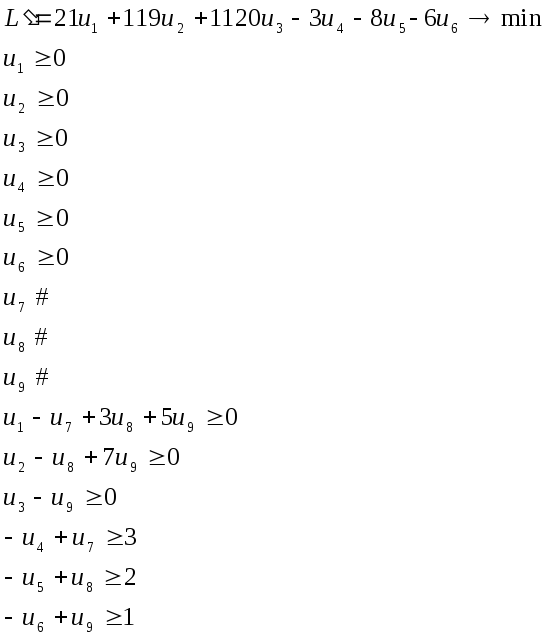5 Анализ на чувствительность

Анализ модели на чувствительность представляет собой исследование влияния изменения исходных параметров модели на оптимальное решение. Для задачи ЛП этими параметрами являются коэффициенты целевой функции, правые части ограничений и коэффициенты при переменных в ограничениях задачи.

Для этого для прямой задачи составим двойственную.

Прямая задача	Двойственная задача

Зная оптимальное решение прямой задачи, найдем оптимальное решение двойственной. По следствию из теоремы о дополняющей нежесткости имеем:

Решая систему, получим:

Отсюда видно, что, изменяя N1 = 21 и N2 = 119, значение целевой функции не измениться, не изменится также оптимальное решение:

Изменим коэффициент N₃ на , тогда

Т.е. новое оптимальное значение будет x^* = (3, 17, 1120+), y^* = (3, 8, 986+) и значение целевой функции будет 1011+.

Изменим коэффициент d₁ на , получим:

Таким образом, получим, что оптимальное значение будет x^* = (3+, 17+, 1120), y^* = (3+, 8, 986-26), значение целевой функции будет = 1011-23. Получаем, что при N<135 система не имеет решения.

Изменим коэффициент d₂ на , получим:

Т.е. новое оптимальное значение будет x^* = (3, 17+, 1120), y^* = (3, 8, 986-7) и значение целевой функции будет 1011-5. Т.е. при >202 система не имеет решения.

Изменим коэффициент d₃ на , получим:

Т.е. при изменении d₃ ничего не меняется.

Увеличим с₁ на , получим:

Т.е. получаем, что оптимальное значение прямой задачи не меняется, а значение целевой функции = 1001+3.

Увеличим с₂ на , получим:

Т.е. получаем, что оптимальное значение прямой задачи не меняется, а значение целевой функции = 1001+8.

Увеличим с₃ на , получим:

Т.е. получаем, что оптимальное значение прямой задачи не меняется, а значение целевой функции = 1001+986. Получаем, что при  = -1, значение целевой функции = 229.

Изменим a₁₂ на , тогда получим:

Т.е. этот коэффициент изменит оптимальное решение: x^* = (3, 17+3, 1120), y^* = (3, 8, 986-21), значение целевой функции тоже изменится: L = 1011-21.

Изменим a₁₃ на , тогда получим:

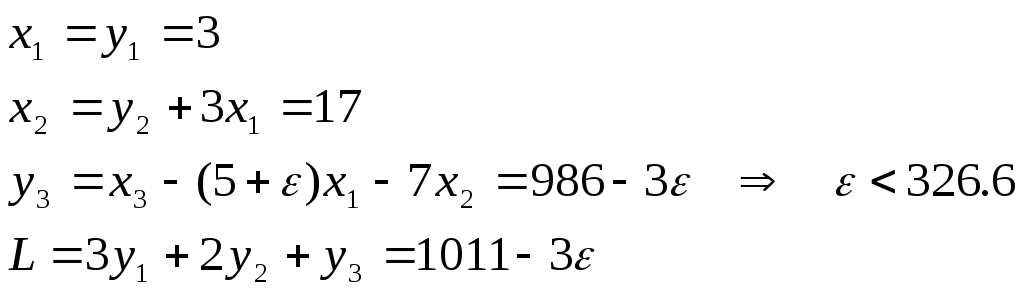
Т.е. этот коэффициент изменит оптимальное решение: x^* = (3, 17, 1120), y^* = (3, 8, 986-3), значение целевой функции тоже изменится: L = 1011-3.

Изменим a₂₃ на , тогда получим:

Т.е. этот коэффициент изменит оптимальное решение: x^* = (3, 17, 1120), y^* = (3, 8, 986-17), значение целевой функции тоже изменится: L = 1011-17.

Изменим a₂₁ на , тогда получим:

Т.е. изменение этого коэффициента приведет к неразрешимости задачи.

Изменим a₃₁ на , тогда получим:

Т.е. этот коэффициент изменит оптимальное решение: x^* = (3+1120, 17+3360, 1120),

y^* = (3, 8, 986-29120), значение целевой функции тоже изменится: L = 1011-29120.

Изменим a₃₂ на , тогда получим:

Т.е. этот коэффициент изменит оптимальное решение: x^* = (3, 17+11200, 1120),

y^* = (3, 8, 986-7840), значение целевой функции тоже изменится: L = 1011-7840.

Список использованных источников

1. Дегтярев Ю.И. Исследование операций. - М.: Высшая школа, 1986. – 224с.

2. Зайченко Ю.П. Исследование операций. - Киев: Высшая школа, 1979.

3. Волков И.К., Загоруйко Е.А. Исследование операций. – М:. Издательство МГТУ им. Баумана, 2000.

15