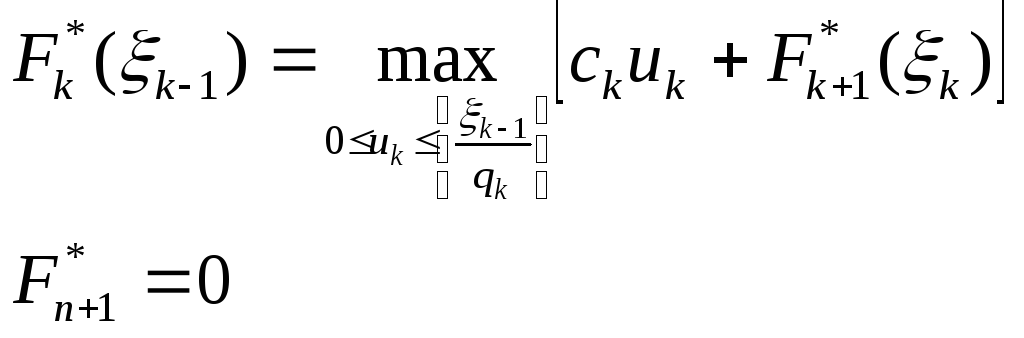ТПР_шпоры2

1. Формула нижней и верхней цены игры.

2. Понятие смешанных стратегий в матричной игре.

Смешанной стратегией (с.с.) игрока в матричной игре называется вероятностное распределение на множестве его ч.с.

.

.

1. Математическая модель задачи о назначениях.

.

, ,

, ,

, ,

3. Понятие смешанных стратегий в матричной игре.

Смешанной стратегией (с.с.) игрока в матричной игре называется вероятностное распределение на множестве его ч.с.

.

.

4. задача линейного программирования для I игрока в смешанных стратегиях.

5. задача линейного программирования для II игрока в смешанных стратегиях.

5. Функция выигрыша в смешанных стратегиях.

.

2. Теорема Неймана.

Теорема (о минимаксе). Для любой матричной игры имеет место равенство Другими словами, любая матричная игра разрешима в с.с.

2. Задача выбора.

В неотрицательной матрице A_ij>=0 (квадратной матрице) необходимо выбрать в каждой строчке и в каждом столбце ровно по 1 максимальному элементу, чтобы их сумма была максимальна. Если матрица Х=х1..xn допустима то в каждой строчке и в каждом столбце ровно по 1 единице. В целевой функции это означает что в каждой строчке и столбце из матрице С берется по 1 элементу.

3. Подготовительный этап алгоритма венгерского метода.

1. Находим максимальный элемент в каждом столбце матрицы .

2. Для каждого столбца все его элементы последовательно вычитаем из максимального, а результат оставляем в соответствующей позиции.

3. Из всех элементов каждой строки вычитаем минимальный элемент этой строки. В результате получаем матрицу с неотрицательными элементами, в каждой строке и в каждом столбце которой имеется по меньшей мере один нуль.

4. Помечаем независимые нули символом "*" по схеме:

а) в первом столбце помечаем произвольный нуль;

б) во втором столбце помечаем (если найдется) тот нуль, в строке которого нет нуля, помеченного "*";

в) аналогично просматриваем один за другим все столбцы матрицы .

4. Эквивалентные матрицы

Две матрицы и назовем эквивалентными , если, . Задачи о назначениях, определяемые эквивалентными матрицами, называются эквивалентными.

5. определение независимых нулей

Нулевые элементы матрицы называются независимыми нулями, если для любого нуля , , строка и столбец, на пересечении которых лежит этот нуль, не содержат других нулевых элементов

6. Критерий завершения алгоритма венгерского метода.

Как только количество независимых нулей становится равным , задача о назначениях решена: оптимальный вариант определяется позициями независимых нулей в последней из матриц, эквивалентных исходн матрице .

7. выделенные элементы матрицы.

Выделенные элементы матрицы - это элементы строк или столбцов, помеченных знаком +. Все остальные элементы матрицы - невыделенные элементы.

1) содержательная постановка задачи Коммивояжера.

Имеется городов, занумерованных числами от 1 до . Расстояния между любой парой городов известны и составляют . Если между городами и нет дороги, то . По тем же соображениям . Вообще говоря, (путь в одну сторону не обязательно совпадает с путем, пройденным в обратную сторону). Коммивояжер (бродячий торговец), выезжая из какого-либо города, должен посетить все города, побывав в каждом ровно один раз, и вернуться в исходный город. Объезд городов, удовлетворяющий этим требованиям, называется маршрутом коммивояжера. Под длиной маршрута понимается сумма длин всех входящих в него переездов из города в город.

Необходимо определить маршрут минимальной длины.

1.выбор множества для ветвления.

На первом шаге это множество . Его нижняя оценка . На остальных шагах из числа кандидатов на ветвление (из множества висячих вершин дерева ветвления) выбирается множество с наименьшей оценкой.

1. Критерий выбора дуги для ветвления.

1. Общая постановка задачи нелинейной оптимизации.

f (x₁,x₂,…,x_n) max(min)

g_i(x₁,x₂,…,x_n) b_i (i=1…m)

x_i  0 (i=1…n),

где f и g_i - некоторые функции переменных x₁…x_n.

2. Задачи квадратичного программирования.

3. Задача выпуклого программирования.

4. Задача линейного программирования в терминологии общей задачи.

f (x₁,x₂,…,x_n) max(min)

g_i(x₁,x₂,…,x_n) b_i (i=1…m)

x_i  0 (i=1…n),

где f и g_i - некоторые линейные функции переменных x₁…x_n.

5. Условие единственности решения задачи дополнительности.

Если матрица P положительная определена, то линейная задача дополнительная, имеет единственное решение z при любом векторе q.

6. Общая итерационная схема решения задачи МП (3 п).

1)F₀(х^к+1)<F₀(x^k)

2),D- допустимая облать.

3)Существует х*=

7. Определение релаксационной последовательности.

Последовательность х^к называется релаксац, в которой выполняются св-ва из 6.

8. Задача одномерной минимизации для выбора величины шага αк.

9. Методы решения задач одномерной минимизации.

1)Выделение (уточнение) отрезка на котором содержится минимум

1)Деление отрезка пополам

2)Метод золотого сечения

3)Метод Фибоначчи

10. Определение линейной задачи дополнительности.

11. Методы решения задачи стохастического программирования (прямые и непрямые).

Прямые используют информацию о значениях функции . Непрямые: если удается выписать явные функции то задачи стохастического программирования становятся нелинейными задачами.

12. Задача условной оптимизации.

13. Задача безусловной оптимизации.

14. Условие для выбора вектора направлений S^k.

15. Условие допустимого направления S^k.

Направление S^k называется дополнительным, если выполняется условие

16. Выбор величины шага α^k вдоль направления S^k

17. Определение активных ограничений

18. Прогрессивное направление

Это направление, которое с градиентом функции образует тупой угол, вдоль которого функция убывает.

19. Возможное направление

Это направление, которое одновременно допустимо (сохраняет допустимость) и прогрессивно (сохраняет убывание)

1)

2)

20. Необходимое условие минимума

21. Обобщенная задача Лагранжа

22. Метод множителей Лагранжа для задачи с ограничениями равенствами

23. Определение ε активных ограничений

Ипсилон активные ограничения – это такие номера i, для которых .

24. Задача ЛП для нахождения допустимого направления

25. каноническая задача выпуклого программирования

26. Свойства канонической задачи ВП

Оптимальное решение КЗВП, если оно существует, достигается на границе области.

27. Общая формулировка вариационного неравенства

1. Принцип оптимальности динамического программирования

Оптимальное управление обладает таким свойством, что каково бы ни было начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет процесс в конце данного шага.

2. Общее уравнение Беллмана

, ,

Уравнение для последнего шага

3. Уравнение Беллмана для задачи распределения ресурсов

, ,

, (так как

4. Уравнение Беллмана для задачи о замене оборудования

5. Уравнение Беллмана для задачи о рюкзаке

Уравнение Беллмана для задачи о пожаре