7.3 Схемы частотной модуляции

На практике применяются два метода ЧМ:

1. косвенный;

2. прямой.

Косвенный метод заключается в преобразовании фазовой модуляции в частотную. С этой целью в схеме фазовой модуляции необходимо получить такие модулированные колебания, у которых девиация фазы была бы обратно пропорциональна частоте , как при ЧМ, для которой справедливо условие:

(индекс частотной модуляции).

При выполнении этого условия девиация частоты будет прямо пропорциональна амплитуде модулирующего колебания, и частота будет изменяться по закону этого колебания, т.е.

(7.2)

Преобразование можно осуществить, если на вход фазового модулятора (ФМ) подать не первоначальное модулирующее напряжение , а напряжение, преобразованное так, чтобы после фазовой модуляции можно было получить колебания с частотой, меняющейся по закону . Если обозначить преобразованное модулирующее напряжение через , то при ФМ

при этом частота:

Для выполнения условия (7.2) необходимо, чтобы

тогда

Следовательно, связь модулирующего напряжения и искомого напряжения должна быть следующей:

т.е. преобразование модулирующего напряжения на входе фазового модулятора заключается в его интегрировании.

Преобразование производится с помощью интегрирующих цепей (рис. 7.5).

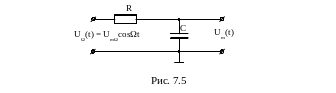
где R>>

Если напряжение на входе интегрирующей цепи

то на её выходе, т.е. на емкости С

т.е. напряжения и сдвинуты по фазе на - т.к. в выражение входит множитель -j.

По этим причинам мгновенное напряжение меняется по закону, если меняется по закону .

Таким образом, передатчик с ЧМ по принципу косвенной модуляции отличается от передатчика с ФМ наличием интегрирующей цепи на выходе амплитудного модулятора.

Косвенный метод ЧМ даёт высокую стабильность несущей частоты , т.к. в генераторе осуществляется кварцевая стабилизация частоты.

Недостатки:

1. Сложность схемы передатчика.

2. Необходимость многократного деления и умножения частоты.

Это ограничивает их широкое применение и используются косвенные методы лишь в мощных стационарных передатчиках.

Прямой метод ЧМ достигается прямым воздействием на контур автогенератора.

Основным недостатком является низкая стабильность частоты. Для повышения стабильности применяют АПЧ. Такой метод (т.е. прямой метод ЧМ) широко применяется на практике, т.к. позволяет осуществить глубокую широкополосную модуляцию.

Вопросы для самопроверки

1. Что такое индекс фазовой модуляции?

2. Что такое индекс частотной модуляции?

3. Как прийти от фазовой модуляции к частотной?

4. Нарисуйте схему фазовой модуляции без преобразования частоты.

5. Нарисуйте схему фазовой модуляции с преобразованием частоты.

6. Достоинства частотной модуляции.

7. Недостатки фазовой модуляции.

Раздел 8 прямой метод чм с варикапом

В схемах ЧМ с варикапом используется свойство p-n перехода закрытого диода, когда емкость перехода зависит от величины запирающего напряжения, приложенного к переходу. Варикапы можно применять на частотах до нескольких сотен МГц [2,4,6].

Достоинство: малые габариты.

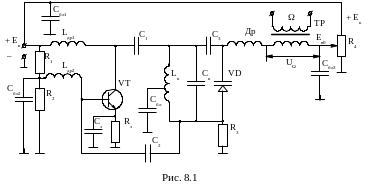
Схема автогенератора с управляемым варикапом приведена на рис. 8.1.

Варикап, т.е. диод VD включается параллельно контуру автогенератора. Начальное смещение на диод подается с потенциометра . Величина этого смещения должна быть такой, чтобы диод был закрытым при наличии ВЧ напряжения и модулирующего напряжения , снимаемого с вторичной обмотки трансформатора, т.е.

.

Величина выбирается из условия

где - зарядная емкость диода. На рис.8.2 приведена вольт-фарадная характеристика варикапа.

Рис. 8.2

Рис. 8.3

Эквивалентная схема варикапа приведена на рис. 8.3, где

r - сопротивление p – n перехода;

- сопротивление выводов диода;

- емкость между выводами;

- диффузионная емкость;

- зарядовая емкость.

При знаке – у значения и , а , тогда упрощенная эквивалентная схема варикапа следующая (рис. 8.4):

Емкость определяется наличием объемного заряда в запирающем слое и мало зависит от частоты и температуры.