Глава 9. Динамический синтез и анализ манипуляционных систем промышленных роботов

Динамический синтез (обратная задача динамики) манипуляционных систем промышленных роботов заключается, кроме прочего, в определении обобщенных сил, действующих в приводах каждой степени подвижности и необходимых для обеспечения требуемого закона движения схвата по заданной траектории.

При динамическом анализе (прямая задача динамики) по известным обобщенным силам, действующим в каждой из степеней подвижности манипулятора, определяют законы движения звеньев по обобщенным координатам.

Для решения этих задач будем использовать уравнение Лагранжа 2-го рода:

, (i=1,…,n),

где L – функция Лагранжа, вычисляемая по формуле L = К–П, здесь: К и П – соответственно полные кинетическая и потенциальная энергии подвижных звеньев манипулятора в данный момент времени; F_i – обобщенная сила, действующая в i-й степени подвижности.

Исходными данными для динамического синтеза манипулятора являются линейные и угловые скорости соответствующих точек и звеньев манипулятора, определяемые в ходе решения прямой или обратной задач кинематики, моменты инерции и массы звеньев, а также некоторые другие параметры.

В соответствии с приведенным уравнением Лагранжа 2-го рода алгоритм определения обобщенных сил сводится к последовательному выполнению следующих операций:

1. Определение кинетической энергии подвижных звеньев манипулятора.

2. Определение потенциальной энергии подвижных звеньев манипулятора.

3. Определение функции Лагранжа L.

4. Почленное определение составляющих уравнения Лагранжа 2-го рода путем дифференцирования функции Лагранжа по обобщенным скоростям и по времени, а затем – по обобщенным координатам.

В результате выполнения этого алгоритма будут получены зависимости между обобщенными силами и обобщенными ускорениями, скоростями и координатами, которые (зависимости) можно в общем виде представить следующим образом:

Полученные n дифференциальных уравнений можно использовать как для динамического анализа, так и для динамического синтеза манипулятора. При этом при динамическом синтезе обобщенные силы определяются непосредственно по приведенным уравнениям путем прямых расчетов, так как все параметры в левых частях уравнений оказываются известными, а при решении задач динамического анализа, когда известны лишь обобщенные силы F_i(t), приходится приведенные уравнения рассматривать как систему n обыкновенных дифференциальных уравнений второго порядка и решать ее (систему) тем или иным численным методом, например методом Рунге-Кутта. Результатом решения системы дифференциальных уравнений будут законы движения ,ивсех звеньев по обобщенным координатам.

Поясним решение задач динамики на примере двух простых манипуляторов.

Манипулятор с двумя степенями подвижности, работающий в ангулярной (угловой) системе координат (рис. 9.1).

При динамическом ана­­лизе и синтезе данного манипулятора будем считать известными кинематические размеры манипулятора (дли­на b₁ звена 1; расстояния а₁ и а₂ до центров масс), моменты инерции J₁, J₂ и массы m₁, m₂ звеньев.

Определим зависимости между абсолютными и обобщенными скоростями манипулятора. Линейные скорости V₁ и V₂ центров масс звеньев 1 и 2 равны:

,

где и – проекции скорости V₂ на оси координат x₀ и y₀.

Так как

и

то

Тогда

Определим полную кинетическую энергию манипулятора

Перегруппируем слагаемые кинетической энергии по обобщенным скоростям:

,

где: ;

;

.

Определим полную потенциальную энергию манипулятора:

, где g – ускорение свободного падения.

Запишем уравнение Лагранжа 2-го рода для каждой степени подвижности:

Найдем выражение составляющих уравнений Лагранжа 2-го рода. Так как потенциальная энергия манипулятора не зависит от обобщенных скоростей, то

Из выражения для определения полной кинетической энергии манипулятора видно, что кинетическая энергия манипулятора не зависит от обобщенной координаты , поэтому

.

При выводе последней формулы надо иметь в виду, что

Определим последнюю из составляющих уравнений Лагранжа 2-го рода.

Собирая полученные выражения в зависимости, выражающие уравнение Лагранжа 2-го рода, после некоторых преобразований получим

При решении задач динамического анализа (прямая задача динамики) эти уравнения следует, как отмечалось, рассматривать в качестве системы дифференциальных уравнений и, интегрируя их численно, определять при известных обобщенных силах F₁ и F₂ законы движения ипо обобщенным координатам и их первые и вторые производные,и,, являющиеся обобщенными скоростями и ускорениями.

Для решения задач динамического синтеза (обратная задача динамики) достаточно по известным ,,,и,и другим параметрам прямым способом вычислить обобщенные силыF₁ и F₂ .

Манипулятор, работающий в цилиндрической системе координат и имеющий три степени подвижности, изображен на рис. 9.2.

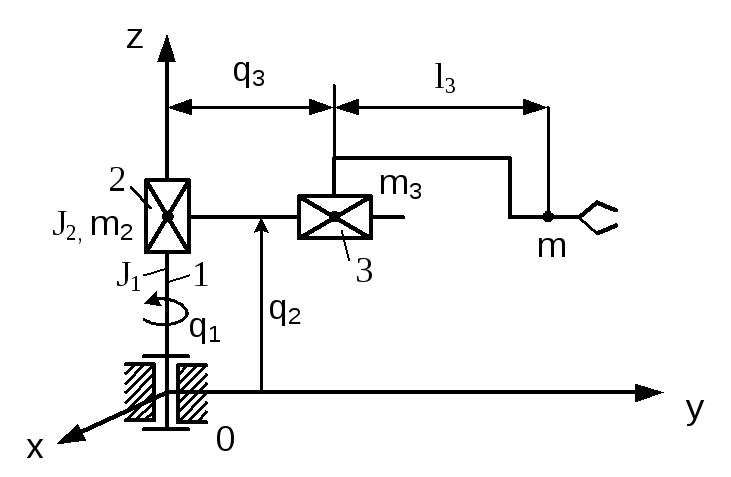
Рис. 9.2

В соответствии с ранее принятым алгоритмом запишем декартовы координаты масс звеньев манипулятора как функции обобщенных координат:

x₂ = 0, y₂ = 0, z₂ = q₂;

x₃ = q₃cosq₁; y₃ = q₃sinq₁; z₃ = q₂;

x = (q₃+l₃)cosq₁; y = (q₃+l₃)sinq₁; z = q₂.

Продифференцировав полученные зависимости по времени, определим проекции скоростей центров масс на декартовы координаты:

; ; ; ;

; ;

; ; .

Определим квадраты полных скоростей центров масс:

;

Запишем выражение для кинетической энергии манипулятора:

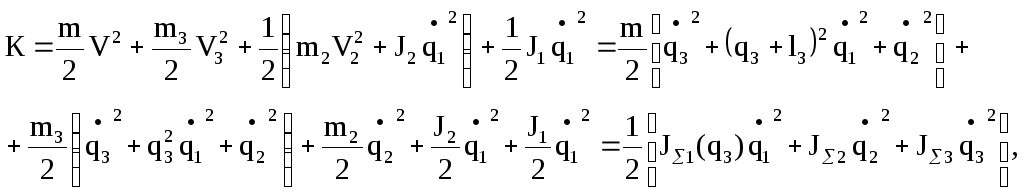
где

Потенциальная энергия манипулятора есть функция обобщенной координаты q₂: где g = 9,81 м/с².

Запишем функцию Лагранжа L = K–П и уравнения Лагранжа 2-го рода для каждой степени подвижности:

, (i=1, 2, 3).

Дифференцируя соответствующим образом функцию Лагранжа, определим составляющие уравнения Лагранжа 2-го рода, расположенные в ее левой части.

Для 1-й степени подвижности:

Кинетическая и потенциальная энергии манипулятора не зависят от обобщенной координаты q₁, поэтому

.

Для 2-й степени подвижности:

Кинетическая энергия манипулятора не зависит от обобщенной координаты q₂, поэтому

Для 3-й степени подвижности:

Потенциальная энергия манипулятора не зависит от обобщенной координаты q₂, поэтому

Подставляя полученные составляющие в уравнения Лагранжа 2-го рода, запишем систему уравнений динамики манипулятора:

Как и раньше, рассчитав из каких-либо условий, например из условия реализации заданной траектории путем решения обратной задачи кинематики законы ,и, можно определить требуемые при известных массах и моментах инерции звеньев силовые воздействия привода.

При проектировании манипуляционных систем промышленных роботов наибольший интерес представляет обратная задача динамики, когда по известным (требуемым для обеспечения заданного движения схвата) законам изменения обобщенных координат следует определить необходимые для этого обобщенные силы.

В связи с тем, что при решении обратной задачи кинематики манипуляторов, как правило, используются численные методы и ввиду сложности зависимостей для расчета полных кинетических и потенциальных энергий многозвенных манипуляторов произвольной структуры, уравнения Лагранжа 2-го рода, описывающие динамику таких манипуляторов, также приходится решать численно, например, с использованием центральных разностных схем.