
- •Мехатронные и робототехнические системы
- •Введение
- •Глава 1. Предпосылки развития, основные понятия и принципы построения мехатронных устройств
- •Предпосылки развития мехатроники
- •Основные понятия и определения мехатроники
- •Принципы построения, признаки и состав мехатронных систем
- •Глава 2. Применение мехатронных машин
- •2.1. Мобильные мехатронные роботы для инспекции и ремонта подземных трубопроводов
- •2.2. Лазерный робототехнический комплекс
- •2.3. Робототехнический комплекс механообработки
- •2.4. Технологические машины – гексаподы
- •2.5. Транспортные мехатронные средства
- •Глава 3. Структура и принципы интеграции мехатронных систем
- •Глава 4. Проблемы и современные методы управления мехатронными модулями и системами
- •4.1. Принципы построения систем интеллектуального управления в мехатронике
- •4.2. Иерархия управления в мехатронных системах
- •4.3. Системы управления исполнительного уровня
- •4.3.1. Адаптивное регулирование по эталонной модели
- •4.3.2. Нечеткие регуляторы исполнительного уровня
- •4.3.3. Системы управления тактического уровня. Система контурного силового управления технологическим роботом
- •4.3.4. Способы программирования траекторий технологических роботов
- •4.3.5. Интеллектуальные системы управления на основе искусственных нейронных сетей
- •Глава 5. Области применения роботов и робототехнических систем. Классификация промышленных роботов и их технические характеристики
- •5.1. Классификация роботов
- •5.2. Техническая характеристика пр (гост 25378 - 82)
- •Глава 6. Структура, классификация и основы кинематики манипуляционных систем промышленных роботов
- •6.1. Структура манипуляторов промышленных роботов
- •6.2. Переносные и ориентирующие степени подвижности манипулятора
- •6.3. Основы кинематики манипуляторов роботов
- •Положение I-го звена относительно предыдущего (I-1)-го устанавливается с помощью обобщенной координаты qi (рис. 6.6):
- •6.4. Однородные координаты. Матрица перехода 4×4 кинематической пары
- •6.5. Определение ориентации звеньев манипуляторов с использованием углов Эйлера
- •Глава 7. Прямая задача кинематики манипуляторов роботов. Абсолютные скорости и ускорения в манипуляционных системах промышленных роботов
- •7.1. Теоретические вопросы решения прямой задачи
- •7.2. Решение прямой задачи кинематики манипуляторов при позиционном (цикловом) управлении
- •7.3. Определение абсолютных скоростей и ускорений точек и звеньев манипулятора
- •Глава 8. Обратная задача кинематики манипуляторов роботов
- •8.1. Обратная задача кинематики манипуляторов роботов при контурном управлении
- •8.2. Решение обратной задачи кинематики манипуляторов на основе линейной зависимости между абсолютными и обобщенными скоростями (управление по скорости)
- •Глава 9. Динамический синтез и анализ манипуляционных систем промышленных роботов
- •Глава 10. Назначение, состав и классификация робототехнических комплексов
- •10.1. Назначение робототехнических комплексов
- •10.2. Состав и классификация робототехнических комплексов
- •Глава 11. Траектории манипуляторов роботов в составе робототехнических комплексов
- •Компоновка ртк и возможные траектории схвата манипулятора
- •11.2. Анализ местных (частных) траекторий манипулятора
- •11.3. Особенности использования нескольких пр в одном ртк
- •11.4. Межстаночные траектории как функции числа схватов и организации производственной сцены
- •Глава 12. Планирование траекторий схвата манипулятора на основе сплайн – функций
- •12.1. Планирование траекторий при ограниченном числе
- •Опорных точек
- •12.2. Общие случаи планирования траекторий в пространстве обобщенных координат
- •Глава 13. Применение робототизированных технологических комплексов в механообрабатывающем производстве
- •13.1. Требования к технологическим процессам, реализуемым в ртк
- •13.2. Требования к деталям, обрабатываемым в ртк
- •13.3. Требования к технологическому оборудованию, используемому в ртк
- •13.4. Требования к промышленным роботам, включаемым в состав ртк
- •13.5. Требования к вспомогательному и транспортно-накопительному оборудованию, включаемому в ртк
- •13.6. Требования к ртк
- •13.7. Общие характеристики и особенности ртк механообработки
- •Библиографический список
- •Оглавление
8.2. Решение обратной задачи кинематики манипуляторов на основе линейной зависимости между абсолютными и обобщенными скоростями (управление по скорости)
Как известно, положение схвата манипулятора однозначно определяется его обобщенными координатами, а именно:
|
|
(8.6) |
где:
![]() – вектор абсолютных координат схвата;
– вектор абсолютных координат схвата;
![]() –вектор
обобщенных координат манипулятора;
–вектор
обобщенных координат манипулятора;
![]() –число
степеней подвижности манипулятора.
–число
степеней подвижности манипулятора.
Дифференцируя (8.6) по времени, получим
|
|
(8.7) |
где
![]() – матрица Якоби размерностью
– матрица Якоби размерностью![]() для преобразования (8.7).
для преобразования (8.7).
В
терминах рассматриваемой нами обратной
задачи кинематики манипуляционных
систем матрица Якоби (размерностью
![]() )
имеет вид:
)
имеет вид:

Зависимость (8.7) более подробно можно представить следующим образом:
|
|
(8.8) |
Зависимости
(8.7) и (8.8) показывают, что между абсолютными
скоростями
![]() и обобщенными скоростями
и обобщенными скоростями![]() существует линейная связь, однако
коэффициенты в этой линейной связи
переменные, так как элементы матрицы
Якоби
существует линейная связь, однако
коэффициенты в этой линейной связи
переменные, так как элементы матрицы
Якоби![]() ,
которые образуют эти коэффициенты в
различных сочетаниях, есть величины
переменные.
,
которые образуют эти коэффициенты в
различных сочетаниях, есть величины
переменные.
Выражение
(8.7) представляет собой прямую скоростную
задачу и её решение при известных
(заданных) функциях
![]() не представляет собой принципиальных
трудностей.
не представляет собой принципиальных
трудностей.
Решим
зависимость (8.7) относительно обобщенных
скоростей
![]() ,
а именно:
,
а именно:
|
|
(8.9) |
Эта зависимость и есть решение обратной задачи по скорости, которая часто используется для управления манипуляционным роботом в режиме on-line.
При
этом вектор обобщенных координат Q
является неизвестным и значения
![]() приходится для данного момента времени
(рассчитываемого момента реального
времени) брать с датчиков обратной
связи, фиксирующих текущее положениеi-го
звена относительно (i-1)-го,
то есть значение
приходится для данного момента времени
(рассчитываемого момента реального
времени) брать с датчиков обратной
связи, фиксирующих текущее положениеi-го
звена относительно (i-1)-го,
то есть значение
![]() .
.
В
выражении (8.9)
![]() есть обратная матрица по отношению к
матрице Якоби
есть обратная матрица по отношению к
матрице Якоби![]() .
.
Рассмотрим более подробно последовательность решения прямой и обратной скоростных задач на примере простого манипулятора с двумя степенями подвижности (рис. 8.9).

Рис. 8.9. Манипулятор с двумя степенями подвижности
Прямая задача о положении:
|
|
(8.10) |
При
этом: ![]()
![]() .
.
Обратная задача о положении:
|
|
(8.11) |
Даже для столь простого манипулятора решение обратной задачи представляет собой нелинейные зависимости.
Для
более сложных манипуляторов, как правило,
найти зависимость
![]() в явном виде не представляется возможным.
в явном виде не представляется возможным.
Однако
зависимость
![]() необходима для управления манипуляционным
роботом, так как требуемое движение
схвата обеспечивается соответствующими
движениями звеньев манипулятора по
обобщенным координатам:
необходима для управления манипуляционным
роботом, так как требуемое движение
схвата обеспечивается соответствующими
движениями звеньев манипулятора по
обобщенным координатам:![]()
![]() .
.
В
то же время, как было указано раньше
(см. зависимость (8.9)), между обобщенными
скоростями
![]() и абсолютными скоростями
и абсолютными скоростями![]() существует линейная связь с переменными
коэффициентами. Именно поэтому часто
и переходят к управлению по скоростям.
существует линейная связь с переменными
коэффициентами. Именно поэтому часто
и переходят к управлению по скоростям.
Получим требуемые зависимости между обобщенными и абсолютными скоростями для рассматриваемого нами двухзвенного манипулятора, используя общий подход, не прибегая пока к обратной матрице Якоби.
Пример решается с целью продемонстрировать порядок получения аналитических зависимостей для управления по скоростям, считая это решение обратной задачи в явном виде (подобно выражениям (8.11)) невозможным или нецелесообразным из-за сложности.
Поэтому начнём решение с дифференцирования формул (8.10) по времени
|
|
(8.12) |
Введем обозначения:
|
|
(8.13) |
Тогда:
|
|
(8.14) |
Решим
полученные зависимости (8.13), (8.14)
относительно обобщенных скоростей
![]() и
и![]() .
Получим вначале явную зависимость от
.
Получим вначале явную зависимость от![]() и
и![]() для обобщенной скорости
для обобщенной скорости![]() .
Для этого умножим первую из зависимостей
(8.14) на
.
Для этого умножим первую из зависимостей
(8.14) на![]() ,
а вторую на
,
а вторую на![]() :
:
![]()
Вычтем
из первого выражения второе:
![]() ,
и следовательно:
,
и следовательно:
|
|
(8.15) |
Для
получения явной зависимости относительно
![]() умножим первое из выражений (8.14) на
умножим первое из выражений (8.14) на![]() ,
а второе на
,
а второе на![]() .
Тогда:
.
Тогда:
![]()
Вычитая
из первого выражения второе, получим
![]() .
.
Откуда
|
|
(8.16) |
Упростим
выражения (8.15) и (8.16). Вначале упростим
знаменатель дроби перед
![]() и
и![]() ,
учитывая выражения (8.13),
,
учитывая выражения (8.13),
![]()
Теперь выражения (8.15) и (8.16) можно записать в окончательном виде:
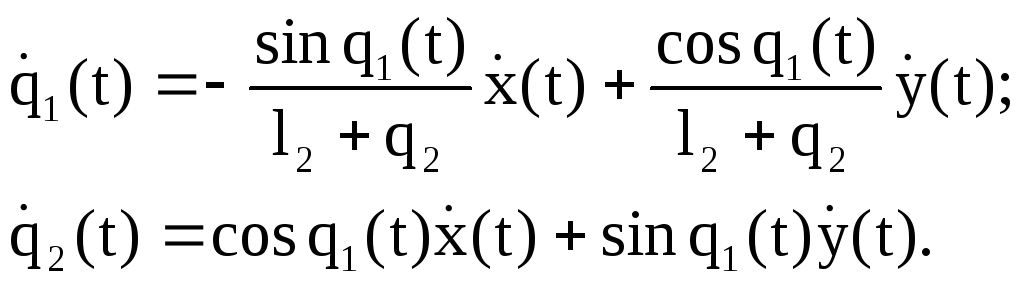
Или компактнее
|
|
(8.17) |
В матричной форме выражения (8.17) имеют вид
|
|
(8.18) |
Что и требовалось получить.
Выражения для обобщенных скоростей в форме (8.17) и (8.18) выше получены обычным путем алгебраических преобразований. Для сложных манипуляторных систем такой подход будет связан с громоздкими преобразованиями.
Для решения рассматриваемой задачи имеется более рациональный подход с использованием обратной матрицы Якоби.
Представим производные (8.12) и (8.14) по времени в виде выражений:
![]()
или в форме матриц:
|
|
(8.19) |
Матрица, являющаяся первым сомножителем в правой части выражения (8.19), есть матрица Якоби.
Следовательно, выражение (8.19) можно записать в виде
|
|
(8.20) |
Убедимся, что первый сомножитель в правой части выражения (8.20) есть матрица Якоби для рассматриваемого манипулятора.
Действительно,
беря частные производные по
![]() и
и![]() от правой части зависимости (8.10), получим
от правой части зависимости (8.10), получим
 .
.
Данное выражение полностью совпадает с соответствующей матрицей выражения (8.19).
Получим обратную матрицу Якоби в следующей последовательности:
Матрица алгебраических дополнений исходной матрицы Якоби:
 .
.
Присоединенная матрица – транспонированная матрица алгебраических дополнений:
 .
.
Определитель исходной матрицы Якоби – Якобиан:
![]() .
.
Обратная матрица Якоби
 .
.
Как видно, полученное выражение полностью совпадает с первым сомножителем правой части зависимости (8.18) и, следовательно, выражение (8.9) полностью обосновано для рассмотренного примера.



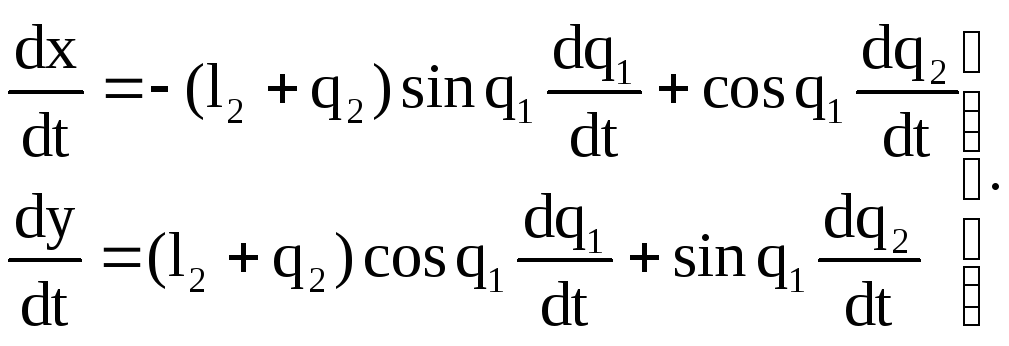
 ;
;
 .
.