Знакочередующиеся числовые ряды.
Ряд называется знакочередующимся, если два любых соседних члена ряда имеют противоположные знаки. Знакочередующиеся ряды могут сходиться абсолютно или условно.
Признак Лейбница. Знакочередующийся ряд сходится если:
А) модули членов
числового ряда являются действительными
числами и составляют монотонно убывающую
последовательность;
Чтобы ряд сходился абсолютно,
необходимо выполнение условий признака
Лейбница и, кроме того, ряд, составленный
из абсолютных величин членов данного
ряда должен быть сходящимся. Если
выполняется признак Лейбница, но не
выполняются условия абсолютной
сходимости, то говорят, что ряд сходится
условно.
Пример:
исследовать знакочередующийся ряд на
сходимость, если общий член ряда
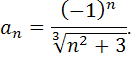
Начнем исследование числового ряда на сходимость с признака Лейбница.
последовательность модулей членов ряда
монотонно убывающая, общий член ряда
при n→∞
стремится к нулю, следовательно, ряд
сходится по признаку Лейбница. Проверим
ряд на абсолютную сходимость. Рассмотрим
знакопостоянный числовой ряд, составленный
из модулей
для
знакопостоянных числовых рядов. Сравним
общий член данного ряда с
Следовательно,
числовой ряд, составленный из модулей
членов данного ряда, также расходится.
А так как признак Лейбница выполняется,
следовательно, заданный для исследования
ряд сходится условно.
сходимость.
По признаку Лейбница
ряд сходится, так как 
а знаменатель при 
,
стремится к бесконечности, т.е.
Ряд, составленный из модулей членов ряда
Т.е. исходный ряд сходится абсолютно.
Пример:
исследовать знакопеременный числовой
ряд
Пример:
исследовать знакочередующийся числовой
ряд
(предел находили по правилу Лопиталя). Исследуем на сходимость ряд из модулей членов числового ряда по интегральному признаку Коши.
Рассмотрим неопределенный интеграл, сделав соответствующую замену переменной, а результат интегрирования подставим в несобственный интеграл.
из
модулей членов исходного ряда, расходится,
т.е. заданный ряд сходится условно.
2. Степенные ряды. Область сходимости.
функциональным рядом. Каждый член этого ряда – функция, зависящая от переменной x и номера члена ряда n.
Степенной ряд –
частный случай функционального ряда,
где функции 
являются степенными функциями переменной
x.
При определенных значениях переменной
x
степенной ряд может сходиться, при
других значениях аргумента
x
может
расходиться.
Теорема
Абеля. Если
степенной ряд сходится при некотором
значении 
,
то он сходится, и при том абсолютно, при
всех значениях 
.
Областью сходимости степенного ряда называется интервал (-R, R) такой, что для всякой точки x, которая лежит внутри этого интервала, ряд сходится, и к тому же абсолютно, а для точек x, лежащих вне интервала, ряд расходится.
если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
Критерий Коши равномерной сходимости ряда: для равномерной
чтобы для любого числа ε>0 существовал такой номер члена ряда N(ε), что при n>N и любом целом p>0 неравенство
выполнялось бы
для всех x
отрезка
.
Действительно, это получается сразу
же, если учесть, что
.
Признак равномерной сходимости Вейерштрасса.
любом n и при всех значениях аргумента x, принадлежащих отрезку .
рядом, то исследуемый степенной ряд равномерно сходится на этом отрезке.
Область сходимости степенного ряда обычно находят с помощью признака Даламбера:
(2.1)
или с помощью признака Коши:
(2.2)
Решая неравенства (2.1) или (2.2) находят диапазон изменения аргумента x, при котором неравенства удовлетворяются. Внутри области сходимости ряды сходятся абсолютно и равномерно.
Пример: определить интервал сходимости степенного ряда и исследовать поведение ряда на концах интервала сходимости.
1. Определим интервал сходимости по признаку Даламбера (2.1).
Рассмотрим
Произведя сокращения, получим:
т.к.
(по 3-ему замечательному пределу), то
получим область сходимости
или
,
т.е. 
и окончательно -3<x<1. Внутри интервала сходимости (-3; 1) исследуемый ряд сходится абсолютно и равномерно.
2. Исследуем поведение ряда на концах интервала сходимости.
а) Пусть х=-3, тогда на левом конце интервала сходимости получим числовой знакочередующийся ряд
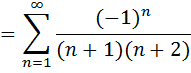
Исследуем полученный знакочередующийся числовой ряд по признаку Лейбница:
;
; 
;
…
Получим, что 
…-
монотонно убывающая последовательность,
составленная из модулей членов числового
ряда. Следовательно, по признаку Лейбница
ряд сходится.
Следовательно,
при 
исходный степенной ряд сходится
абсолютно.
б) Пусть х=1, тогда на правом конце интервала сходимости получим знакопостоянный числовой ряд:
Полученный ряд по признаку сравнения сходится. Ответ: область сходимости [-3;1].
Пример: определить интервал сходимости степенного ряда
Определим интервал сходимости по признаку Даламбера.
Т.к.
,
следовательно,
неравенство справедливо при любых
значениях аргумента x,
т.е. область сходимости ряда (-∞; +∞)
– вся числовая ось.
Пример: найти область сходимости степенного ряда
1. Находим область сходимости ряда по признаку Коши:
Т.к. предел стремится
к единице, то 
,
т.е. область сходимости 
или 
.
Внутри полученной области сходимости ряд сходится абсолютно и равномерно.
2. Исследуем поведение ряда на концах интервала сходимости.
a) Пусть x=4, на левом конце области сходимости получаем знакочередующийся числовой ряд:
Исследуем знакочередующийся числовой ряд по признаку Лейбница:
монотонно убывающая последовательность,
следовательно, по признаку Лейбница
ряд сходится.
Исследуем ряд из модулей членов ряда по интегральному признаку Коши.
следовательно, ряд из модулей членов ряда расходится. Т.е. при x=4 имеем условную сходимость.
б) Пусть x=6.
соответствующий ряду из модулей членов исходного ряда. Но по интегральному признаку Коши такой знакопостоянный числовой ряд расходится, т.е. при x=6 исследуемый ряд расходится.
Ответ: область сходимости заданного ряда [4; 6). На левом конце интервала сходимости при x=4 сходимость условная, точка x=6 в область сходимости не входит. Внутри области сходимости (4;6) исследуемый ряд сходится абсолютно и равномерно.