Государственное образовательное

учреждение высшего профессионального

образования

Московский авиационный институт

(национальный исследовательский университет)

Институт РАДИОВТУЗ МАИ

О.М. Данченко

Индивидуальные задания по курсу «Математический анализ»

Часть 3

Числовые и степенные ряды, ряды и интеграл Фурье.

Рекомендовано Ученым Советом

Института «Радиовтуз МАИ»

в качестве учебного пособия

по выполнению индивидуальных заданий

студентами заочной формы обучения

МОСКВА

2014

Введение.

Предлагаемое учебное пособие предназначено для студентов, выполняющих индивидуальные домашние задания по следующим разделам курса «Математический анализ»: числовые и степенные ряды, ряды и интеграл Фурье.

В разделах 1-3 основное внимание уделено вопросам исследования числовых и степенных рядов на сходимость, определению областей сходимости степенных рядов, а также приобретению навыков использования степенных рядов при приближенных вычислениях. Разделы 4-5 посвящены задачам на ряд Фурье и интеграл Фурье в действительной и комплексной формах.

В вышеуказанных разделах предлагаемого учебного пособия подробно рассматриваются типовые задачи, соответствующие вариантам индивидуальных домашних заданий; приводится краткое изложение теории. Пособие в основном предназначено для студентов заочного отделения, но может быть полезно и студентам дневного отделения при выполнении курсовых и расчетных работ по соответствующим разделам курса «Математический анализ».

В Приложении приводятся вопросы к экзамену, варианты индивидуальных домашних заданий по указанным выше разделам курса «Математический анализ», а также сведения о гиперболических функциях и рекомендуемая литература.

Содержание.

1. Числовые ряды………………………………………………………………

1.1. Знакопостоянные числовые ряды…………………………………………

1.2. Знакочередующиеся числовые ряды………………………………………

2. Степенные ряды. Область сходимости……………………………………

3. Применение степенных рядов к приближенным вычислениям…………

4. Ряды Фурье………………………………………………………………….

4.1. Ряд Фурье для функций с периодом T=2π………………………………..

4.2. Ряд Фурье для функций любого периода T=2l……………………………

4.3. Комплексная форма ряда Фурье……………………………………………

5. Интеграл Фурье………………………………………………………………

5.1. Комплексная форма интеграла Фурье………………………………………

Приложения……………………………………………………………………….

1.Числовые ряды.

Если члены бесконечной числовой последовательности , ,… ,… соединить знаком плюс, то получится выражение 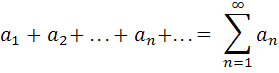(1.1) называемое числовым рядом, где - общий член числового ряда.

- называется частной или частичной суммой (n=1;2;3,…) ряда. Числовой ряд (1.1) называется сходящимся, если сходится последовательность его частичных сумм, т.е. если lim Sn = S при n→∞, где S-сумма ряда. Если последовательность частичных сумм не имеет предела или её предел стремиться к бесконечности, то ряд называется расходящимся.

Критерий Коши. Для того чтобы числовой ряд был сходящимся, необходимо и достаточно, чтобы для любого числа ε >0 существовал такой номер N члена ряда, что при n>N и любом целом p>0, выполнялось бы неравенство Использование критерия Коши на практике весьма затруднительно, поэтому обычно применяют другие признаки сходимости.