2.1 Ортогональная система функций, построенная на основе полиномов Чебышева

Теорема 2.2. Полученные с помощью полиномов Чебышева Т_п(х) функции:

(2.7)

образуют на отрезке [–1, 1] ортогональную систему /3/.

Доказательство. Доказательство /1/ ортогональности сводится к доказательству равенства:

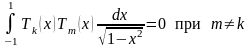(2.8)

При k > 0, m > 0 и k ≠ m, полагая х = cos t и используя формулу (2.3), имеем

(2.9)

а как нам известно из общего курса математического анализа, тригонометрические функции {cos kt} ортогональны на отрезке [–π, π]. Легко проверить, что равенство (2.9) остается справедливым и при k=0, m ≠ 0. Теорема доказана.

2.2 Нормирование системы функций, построенной на основе полиномов Чебышева

Для того, чтоб нормировать систему функций (2.7), вычислим их нормы /1/.

Для этого в формуле (2.8) примем m = k ≠ 0, получим:

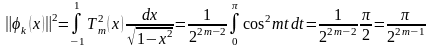
Отсюда, ортонормированная система функций (2.7), полученная с помощью полиномов Чебышева имеет вид:

(2.10)

Коэффициенты Фурье функции f по ортонормированной системе (2.10):

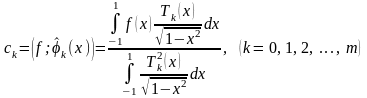(2.11)

3. Примеры аппроксимации функций

Пример 3.1. Функцию 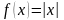на отрезке [–1, 1] квадратично аппроксимировать полиномом Лежандра четвертой степени.

Решение. Полином Q₅(x) ищем в виде частичных сумм ряда Фурье:

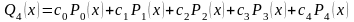(3.1)

где P_k(x) (k = 0, 1, 2, 3, 4) – полиномы Лежандра, а

Так как функция |x| четная и P_k(x) четны при k четном и нечетны при k нечетном, то получаем

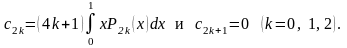
Отсюда используя формулы (1.3), находим

с₁ = с₂ = с₃ = 0.

Подставляя эти значения коэффициентов в формулу (3.1), получим

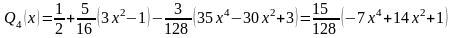
Следовательно,

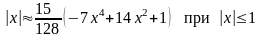
График полученной функции приведен на рисунке 3.1.

Пример 3.2. Найти квадратичное приближение функции в промежутке [–1, 1] полиномом четвертой степени.

Решение. Полином Q₄(х) будем искать в виде

(3.2)

где φ_k(x) (k = 0, 1, 2, 3, 4) – полученные с помощью полиномов Чебышева функции.

Тогда, в условиях нашей задачи и с учетом формулы (2.10), получаем:

Так как Т_2k+1(x) – функции нечетные, а Т_2k(x) – четные, то с_2k+1 = 0 и

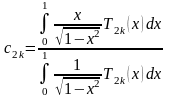
Используя для Т_2k(x) формулу (2.2), имеем:

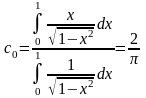
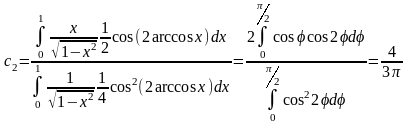
Подставляя найденные значения коэффициентов в формулу (3.2), находим:

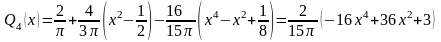
Сравним полученный результат с примером разложения функции по полиномам Лежандра, в котором функция f(x) аппроксимировалась многочленом

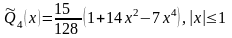
В нашем случае при х = 1 имеем

тогда как

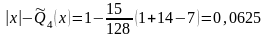
т.е. мы видим, что система функций {φ_k} «ближе» аппроксимировали функцию в точке х = 1. Это видно на рисунке 3.1.

Рисунок 3.1 – Результат примеров аппроксимации (примеры 3.1 и 3.2)

Пример 3.3. Функцию 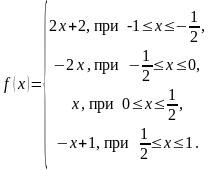на отрезке [–1, 1] квадратично аппроксимировать полиномом Лежандра четвертой степени.

Решение. Полином Q₄(x) ищем в виде частичных сумм ряда Фурье:

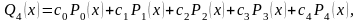(3.3)

где P_k(x) (k = 0, 1, 2, 3, 4) – полиномы Лежандра, а

Для вычисления коэффициентов с_k применен программный продукт MathCad (рабочий документ MathCad'а приведен в приложении С).

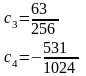
Подставив полученные коэффициенты в формулу (3.3), получаем:

График полученной функции приведен на рисунке 3.2.

Пример 3.4. Найти квадратичное приближение функции в промежутке [–1, 1] полиномом четвертой степени.

Решение. Полином Q₄(х) будем искать в виде

(3.4)

где φ_k(x) (k = 0, 1, 2, 3, 4) – полученные с помощью полиномов Чебышева функции.

Коэффициенты с_k рассчитаны в системе MathCad (см. приложение С).

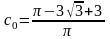
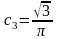
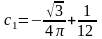
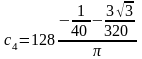
Подставив полученные коэффициенты в формулу (3.4), получаем:

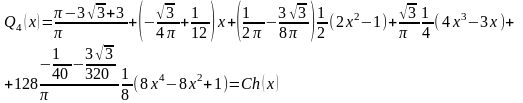
График полученной функции приведен на рисунке 3.2.

Рисунок 3.2 – Результат примеров аппроксимации (примеры 3.3 и 3.4)

Из рисунка 3.2 видно, что аппроксимация не достаточно точная. Чтобы повысить точность аппроксимации, нужно брать большую степень полинома. Это следует из тождества Бесселя:

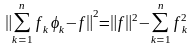
При увеличении n (степени полинома), сумма полинома 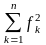не уменьшается, а, следовательно, отклонение не увеличивается.

Приложение А

Первые 10 полиномов Лежандра P_n(x)

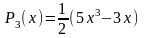
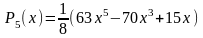
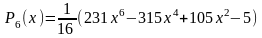
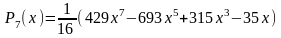
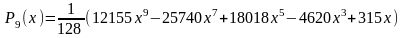
Приложение B

Первые 12 полиномов Чебышева T_n(x)

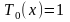
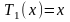
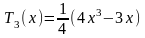
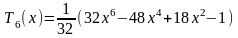
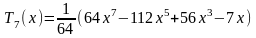
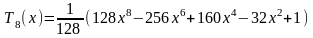
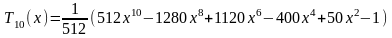
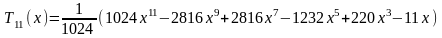
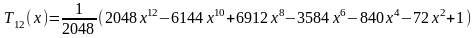
Приложение С

Рабочий документ MathCad'а

Расчет коэффициентов с_k для полиномов Лежандра:

полином ортогональность чебышев лежандр аппроксимация

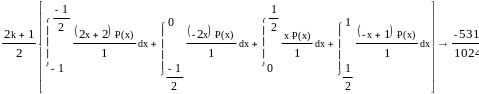
Расчет коэффициентов с_k для полиномов Чебышева:

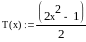
Список используемой литературы

1. Б.П. Демидович, И.А. Марон, Э.3. Шувалова. Численные методы анализа. – М.: Наука, 1967. – 368 с.

2. Л.Д. Кудрявцев. Математический анализ, том 2. – М.: Наука, 1982. – 417 с.

3. В.А. Ильин, В.А. Садовничий, Бл.Х. Сендов. Математический анализ. – М.: МГУ, 1987. – 358 с.

Размещено на Allbest.ru