Размещено на http://www.allbest.ru/

Содержание

Содержание 1

Введение 2

1. Полиномы Лежандра 4

1.1 Ортогональность полиномов Лежандра 6

2.2 Нормирование полиномов Лежандра 8

2. Полиномы Чебышева 11

2.1 Ортогональная система функций, построенная на основе полиномов Чебышева 13

2.2 Нормирование системы функций, построенной на основе полиномов Чебышева 14

3. Примеры аппроксимации функций 16

Приложение А 25

Приложение B 26

Приложение С 27

Список используемой литературы 28

Введение

В курсе математического анализа мы изучали обобщенные ряды Фурье в нормированных пространствах /3/.

Пусть Е – нормированное пространство, норма которого порождена скалярным произведением:

Определение 1. Последовательность φ₁, φ₂, …, φ_n, …, φ_nÎЕ называется ортонормированной системой, если входящие в эту последовательность элементы попарно ортогональны и имеют норму равную единице.

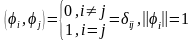
Пусть в пространстве Е задана ортонормированная система {φ_k}_k=1..∞ .

Определение 2. Рядом Фурье элемента f по ортонормированной системе {φ_k} называется ряд вида:

Определение 3. Частичной суммой ряда Фурье называется сумма вида:

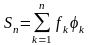
Определение 4. Отклонением элемента f от элемента g по норме пространства Е называется величина, равная .

Теорема. Среди всех сумм вида наименьшее отклонение от элемента f по норме пространства Е имеет частичная сумма ряда Фурье элемента f:

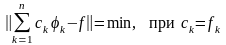
В данной курсовой работе рассматриваются полиномы Лежандра и Чебышева, как примеры ортогональных систем в пространстве непрерывных функций, определенных на [–1, 1] (далее, пространство непрерывных функций будем обозначать как C[–1, 1]). Скалярное произведение в C[–1, 1] вводится как

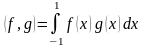
Данный интеграл существует, так как f(x),

g(x)Î C[–1, 1] – пространству непрерывных функций. Таким образом,

1. Полиномы Лежандра

Полиномы Лежандра определяются следующей формулой Родрига 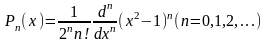/1/:

(1.1)

В частности, имеем:

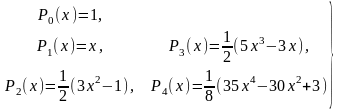(1.2)

Графики этих полиномов для п = 0, 1, 2, 3 и 4 приведены на рисунке 1.1. Первые 10 полиномов Лежандра приведены в приложении А. Из формулы (1.1) видно, что Р_n(х) являются четными функциями при п = 2т и нечетными – при п = 2m + 1; причем Р_n(1)= 1 и Р_n(– 1) = (– 1)ⁿ.

Рисунок 1.1 – Графики первых пяти полиномов Лежандра

Существует много способов определения полиномов Лежандра. Один из них мы уже рассмотрели – задание полиномов формулой Родрига. Теперь рассмотрим еще один немаловажный способ задания полиномов – с помощью рекуррентной формулы. Для этого обратимся к так называемой производящей функции /1/:

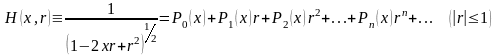(1.3)

Из разложения (1.3) легко получить рекуррентную формулу, связывающую три последовательных полинома Лежандра. Действительно, дифференцируя Н(х, r) по r, имеем

Но с другой стороны

тогда

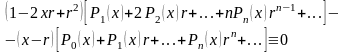
Собирая все члены, содержащие rⁿ, и приравнивая к нулю полученный коэффициент при rⁿ, получаем нужный результат

(1.4)

Формула (1.4) является рекуррентной формулой задания полиномов Лежандра, с помощью которой удобно находить последовательные полиномы Лежандра.