2.6. Взаимное расположение прямых на плоскости

Т еорема 2. Пусть в аффинной системе координат две прямые 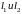заданы своими общими уравнениями

1. Если пересекаются.

2. Если 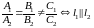условие параллельности двух прямых.

3. совпадают.

Доказательство: Рассмотрим направляющие векторы .

2. Пусть

3. При уравнение 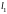получается из уравнения 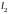умножением левой и правой части на число 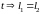. Теорема доказана.

3. Прямая в прямоугольной системе координат

В прямоугольной системе координат справедливы все уравнения полученные в п.2 для аффинной системы координат.

Определение 2. Вектор 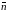называется нормальным вектором прямой , если .

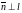Теорема 3. Пусть в прямоугольной системе координат прямая задана общим уравнением . Тогда является нормальным вектором .

Доказательство: По теореме 1 - направляющий вектор . Найдем скалярное произведение 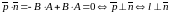. Теорема доказана.

3.1. Уравнение прямой по точке и нормальному вектору

Пусть в прямоугольной системе координат прямая проходит через точку и имеет нормальный вектор . Тогда имеет уравнение 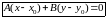- уравнение прямой по точке и нормальному вектору .

3.2. Расстояние от точки до прямой на плоскости

Теорема 4. Пусть в прямоугольной системе координат прямая задана общим уравнением Аx+By+C=0 и - произвольная точка. Тогда расстояние от точки до прямой равно

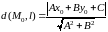
Д оказательство: Пусть - нормальный вектор , по теореме 3 . Рассмотрим точку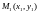 - ортогональную проекцию точки на прямую l.

Тогд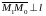а и . Рассмотрим случай .

Тогда 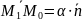, где 0, и

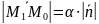(1)

Далее, из равенства векторов следует равенство их координат:

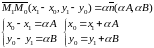
Подставим координаты в уравнение прямой :

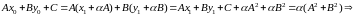
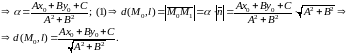
В случае 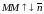имеем 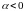, что приведет к формуле:

Теорема доказана.

4. Уравнения плоскости

Положение плоскости в пространстве однозначно определяется либо точкой M₀∈  и двумя неколлинеарными векторами либо тремя точками, принадлежащими .

Направляющим вектором плоскости  называется любой вектор .

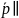Пусть в пространстве задана аффинная система координат .

4.1. Параметрические уравнения плоскости

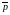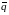Пусть - направляющие векторы плоскости , ∦ . Отложим и от точки .

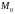1. Покажем, что 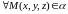, ее координаты удовлетворяют уравнениям (1). Поскольку M₀∈, M∈, тогда лежит в плоскости . Отложим векторы и 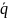от точки M₀, тогда 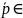, , ∦ . Следовательно и образуют на плоскости  аффинную систему координат. Тогда вектор разлагается по векторам и : 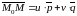для некоторых u, v∈ℝ. Запишем это равенство в координатной форме:

откуда 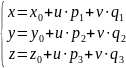(1) - параметрические уравнения плоскости по точке 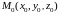и направляющим векторам 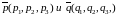, u, v∈ℝ параметры.

2. Аналогично, проводя рассуждения в обратном порядке, можно показать, что если числа x,y,z удовлетворяют уравнениям (1), то соответствующая точка , т.е. (1) – является уравнением плоскости .