
- •Глава IX. Аналитическая геометрия прямых и плоскостей
- •1. Уравнение линии на плоскости
- •2. Уравнения прямой на плоскости
- •2.1. Уравнение прямой по точке и направляющему вектору.
- •2.2. Уравнение прямой, проходящей через 2 точки
- •2.3. Уравнение прямой в отрезках на осях
- •2.4. Уравнение прямой с угловым коэффициентом
- •2.5. Общее уравнение прямой
- •2.6. Взаимное расположение прямых на плоскости
- •3. Прямая в прямоугольной системе координат
- •3.1. Уравнение прямой по точке и нормальному вектору
- •3.2. Расстояние от точки до прямой на плоскости
- •4. Уравнения плоскости
- •4.1. Параметрические уравнения плоскости
- •4.2. Уравнение плоскости по точке и двум направляющим векторам
- •4.3. Общее уравнение плоскости
- •4.4. Уравнение плоскости по трем точкам.
- •5. Плоскость в прямоугольной системе координат
- •5.1. Нормальный вектор плоскости
- •5.2. Уравнение плоскости по точке и нормальному вектору
- •5.3 Угол между плоскостями
- •6. Уравнение прямой в пространстве
- •6.1. Уравнение прямой в пространстве по точке и направляющему вектору
- •6.2. Уравнение прямой в пространстве по двум точкам.
- •6.3. Прямая как линия пересечения двух плоскостей
- •6.4. Расстояние от точки до прямой в пространстве.
- •7. Взаимное расположение прямых и плоскостей
- •7.1. Взаимное расположение двух плоскостей
- •7.2. Взаимное расположение прямой и плоскости
- •7.3. Взаимное расположение двух прямых в пространстве.
Глава IX. Аналитическая геометрия прямых и плоскостей
1. Уравнение линии на плоскости
Пусть на плоскости
задана аффинная система координат
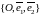 и задано уравнение F(x,
y)=0
(1). На любую пару (x,
y)
действительных чисел можно смотреть
как на координаты точки в данной системе
координат.
и задано уравнение F(x,
y)=0
(1). На любую пару (x,
y)
действительных чисел можно смотреть
как на координаты точки в данной системе
координат.
Определение 1.
Линией
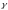 на плоскости определенной уравнением
F(x,y)=0
(1) называется множество всех тех и
только тех точек плоскости, координаты
которых удовлетворяют уравнению (1).
Уравнение (1) при этом называется
уравнением линии
.
на плоскости определенной уравнением
F(x,y)=0
(1) называется множество всех тех и
только тех точек плоскости, координаты
которых удовлетворяют уравнению (1).
Уравнение (1) при этом называется
уравнением линии
.
Другими словами,
уравнение (1)
является уравнением линии
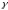 ,
если:
,
если:
1. Все точки линии имеют координаты, удовлетворяющие уравнению (1).
2. Все точки, которые удовлетворяют уравнению (1), принадлежат линии .
2. Уравнения прямой на плоскости
Полагаем,
что на плоскости задана аффинная система
координат
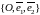 .
.
Определение
2. Вектор
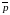 называется направляющим вектором прямой
называется направляющим вектором прямой
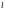 ,
если на прямой
существует направленный отрезок ОА,
такой что
,
если на прямой
существует направленный отрезок ОА,
такой что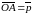 .
.
2.1. Уравнение прямой по точке и направляющему вектору.
Пусть заданы
координаты т.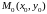 и направляющего вектора
и направляющего вектора
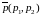 прямой l.
прямой l.

2.1.1. Параметрические уравнения прямой по точке и направляющему вектору.
1. Пусть М(x,y)
– произвольная точка, лежащая на прямой
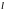 .
Покажем, что ee
координаты удовлетворяют уравнениям
(2).
.
Покажем, что ee
координаты удовлетворяют уравнениям
(2).
Так
как М(x,y)∈
l и
М0(x0,y0)∈
l , то
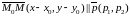 .
Тогда
.
Следовательно,
.
Тогда
.
Следовательно,
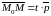 для некоторого
для некоторого
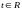 .
В координатной форме:
.
В координатной форме: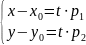
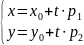 (2)
параметрические
уравнения прямой по точке
и направляющему вектору
.
t
– параметр.
(2)
параметрические
уравнения прямой по точке
и направляющему вектору
.
t
– параметр.
2. Обратно, покажем, что если координаты (x, y) некоторой точки М удовлетворяют (2), то M∈l.
Пусть пара чисел
(x,
y)
удовлетворяет
(2). Это означает, что координаты векторов
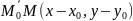 и
и
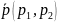 пропорциональны с коэффициентом t.
Тогда
,
то есть
пропорциональны с коэффициентом t.
Тогда
,
то есть
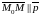 и так как
и так как
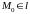 то и
то и
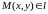 .
.
Из 1 и 2, по определению 1, уравнения (2) задают прямую .
2.1.2. Каноническое уравнение прямой по точке и направляющему вектору.
Выразим из обоих
уравнений (2) параметр t.
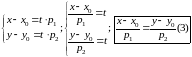
каноническое
уравнение прямой по точке
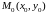 и направляющему вектору
.
и направляющему вектору
.
Замечание 1.
В случае, когда одна из координат
направляющего вектора
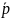 равна нулю, например, p1=0,
то
∥Оу
и
l∥Oy.
Тогда для координат точек М
и М0
справедливо x-x0=0.
Таким образом, числитель и знаменатель
дроби в левой части (3) равны 0. В этой
ситуации допускается формальная запись
равна нулю, например, p1=0,
то
∥Оу
и
l∥Oy.
Тогда для координат точек М
и М0
справедливо x-x0=0.
Таким образом, числитель и знаменатель
дроби в левой части (3) равны 0. В этой
ситуации допускается формальная запись
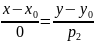 . Однако, для дальнейшей работы с данной
прямой, как правило, переходят от
канонического к параметрическим
уравнениям вида (2).
. Однако, для дальнейшей работы с данной
прямой, как правило, переходят от
канонического к параметрическим
уравнениям вида (2).
2.2. Уравнение прямой, проходящей через 2 точки
Пусть на прямой l
заданы точки
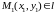 и
и
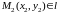 .
Тогда вектор
.
Тогда вектор
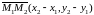 является направляющим вектором для
.
является направляющим вектором для
.

Согласно (3),
уравнение
по точке
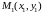 и направляющему вектору
и направляющему вектору
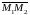 имеет вид
имеет вид
 – уравнение
прямой, проходящей через точки M1(x1,y1)
и M2(x2,y2)
– уравнение
прямой, проходящей через точки M1(x1,y1)
и M2(x2,y2)
2.3. Уравнение прямой в отрезках на осях
Пусть прямая проходит через точки А(а, 0) и В(0, b).

Согласно (4), её уравнение имеет вид:
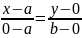 ;
;
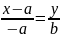 ;
;
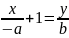 ;
отсюда
;
отсюда
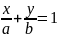 (5) -
уравнение
прямой, отсекающей на координатных осях
отрезки a
и b
соответственно.
(5) -
уравнение
прямой, отсекающей на координатных осях
отрезки a
и b
соответственно.
