
- •Варианты заданий для проведения государственной аттестации по математике в 9 общеобразовательных классах
- •Вариант 1
- •I часть
- •II часть
- •III часть
- •Вариант 2
- •I часть
- •II часть
- •III часть
- •Вариант 3
- •I часть
- •II часть
- •III часть
- •Вариант 4
- •I часть
- •II часть
- •III часть
- •Вариант 5
- •I часть
- •II часть
- •III часть
- •Вариант 6
- •I часть
- •II часть
- •III часть
- •Вариант 7
- •I часть
- •II часть
- •III часть
- •Вариант 8
- •I часть
- •II часть
- •III часть
- •Вариант 9
- •I часть
- •II часть
- •III часть
- •Вариант 10
- •I часть
- •II часть
- •III часть
- •Вариант 11
- •I часть
- •II часть
- •III часть
- •Вариант 12
- •I часть
- •II часть
- •III часть
- •Вариант 13
- •I часть
- •II часть
- •III часть
- •Вариант 14
- •I часть
- •II часть
- •III часть
- •Вариант 15
- •I часть
- •II часть
- •III часть
- •Вариант 16
- •I часть
- •II часть
- •III часть
- •Вариант 17
- •I часть
- •II часть
- •III часть
- •Вариант 18
- •I часть
- •II часть
- •III часть
- •Вариант 19
- •I часть
- •II часть
- •III часть
- •Вариант 20
- •I часть
- •II часть
- •III часть
III часть
Решение заданий 20-21 должно содержать обоснование. В нём необходимо записать последовательные логические действия и их объяснения. Правильное решение каждого задания оценивается в четыре балла.
20. Два
автомобиля выезжают одновременно из
одного города в другой. Скорость первого
на
км/ч
больше скорости второго. Поэтому первый
автомобиль прибывает на место на
час
раньше. Найдите скорость каждого
автомобиля, если расстояние между
городами
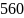 км.
км.
21. Объем
конуса равен
 см3,
а его высота –
см.
Вычислите площадь боковой поверхности
конуса.
см3,
а его высота –
см.
Вычислите площадь боковой поверхности
конуса.
Вариант 7
I часть
Задания 1-15 имеют по четыре варианта ответов, из которых только один ответ правильный. Выберите правильный, на Ваш взгляд, ответ. Правильное решение каждого задания оценивается одним баллом.
1. Сократите
дробь
 .
.
А) ; Б) ;
В)
 ; Г)
; Г)
 .
.
2.
суммы чисел
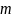 и
и
 равно
равно
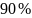 разности чисел
и
.
Найдите сумму чисел
и
,
если разность утроенного числа
и половины числа
равна 65.
разности чисел
и
.
Найдите сумму чисел
и
,
если разность утроенного числа
и половины числа
равна 65.
А) ; Б) ;
В)
; Г)
 .
.
3. Сравните
числа
 и
и
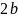 ,
если
,
если
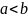 .
.
А)
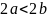 ; Б)
; Б)
 ;
;
В)
 ; Г)
; Г)
 .
.
4. Решите
систему уравнений
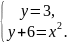
А)
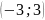 ; Б)
,
;
; Б)
,
;
В)
; Г)
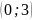 ,
.
,
.
5. некоторого числа равны . Найдите это число.
А)
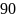 ; Б)
;
; Б)
;
В) ; Г) .
6. Какой из систем неравенств удовлетворяет число ?
А)
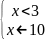 ; Б)
; Б)
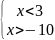 ;
;
В)
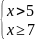 ; Г)
; Г)
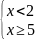 ;
;
7. На каком из рисунков изображен график квадратичной функции?
А


 ) Б) В) Г)
) Б) В) Г)
8. Арбуз в 2,6 раза тяжелее дыни. Определите массу дыни и арбуза, если их общая масса 6,48 кг.
А)
кг
и
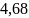 кг; Б)
кг; Б)
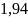 кг
и
кг
и
 кг;
кг;
В)
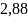 кг
и
кг
и
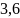 кг; Г)
кг
и
кг; Г)
кг
и
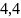 кг.
кг.
9. Определите
количество членов арифметической
прогрессии
 ,
если
,
если
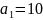 ,
,
 ,
,
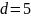 .
.
А)
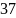 ; Б)
; Б)
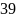 ;
;
В)
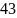 ;
Г)
.
;
Г)
.
10. Среднее
арифметическое двух чисел
 .
Известно, что первое число равно
.
Известно, что первое число равно
 .
Найдите второе число.
.
Найдите второе число.
А)
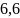 ; Б)
; Б)
 ;
;
В)
; Г)
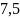 .
.
11. Угол
при вершине равнобедренного треугольника
равна
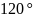 ,
а боковая сторона
см.
Найдите радиус описанной окружности.
,
а боковая сторона
см.
Найдите радиус описанной окружности.
А) см; Б) см;
В) см; Г) см.
12. Если в окружности соединить концы двух взаимно перпендикулярных диаметров, то получим:
А) ромб; Б) квадрат;
В) прямоугольник; Г) параллелограмм.
13. На
плоскости дана точка с координатами
 .
Найдите координаты точки, в которую она
перейдет
при
повороте вокруг начала координат на
угол
по часовой стрелке.
.
Найдите координаты точки, в которую она
перейдет
при
повороте вокруг начала координат на
угол
по часовой стрелке.
А)
 ; Б)
;
; Б)
;
В)
 ; Г)
; Г)
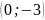 .
.
14. Дан
вектор
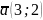 .
Известно, что
.
Известно, что
 .
Найдите координаты точки
.
Найдите координаты точки
 ,
если
,
если
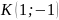 .
.
А)
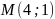 ; Б)
; Б)
 ;
;
В)
 ; Г)
; Г)
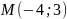 .
.
15. Из точки к плоскости проведен перпендикуляр и наклонная. Длина наклонной равна см, а угол между перпендикуляром и наклонной равен . Найдите длину проекции этой наклонной на плоскость.
А)
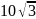 см; Б)
см;
см; Б)
см;
В) см; Г) см.
II часть
Решение заданий 16-19 должно содержать короткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.
16. Докажите,
что система неравенств
 не имеет решений.
не имеет решений.
17. Вкладчик
положил в банк
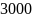 грн.
под
грн.
под
 годовых.
Какой капитал будет у вкладчика через
года?
годовых.
Какой капитал будет у вкладчика через
года?
18. В
с вершинами в точках
 ,
,
 ,
,
 проведена
средняя линия
проведена
средняя линия
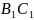 ,
которая параллельна стороне
.
Составьте уравнение прямой
.
,
которая параллельна стороне
.
Составьте уравнение прямой
.
19. Диагонали
подобных многоугольников относятся
как
 соответственно. Сумма их площадей равна
соответственно. Сумма их площадей равна
 см2.
Найти площади многоугольников.
см2.
Найти площади многоугольников.
