7.8 Гиперболалық функцияларды интегралдау

Гиперболалық функцияларды интегралдау үшін төмендегі формулаларды қолдану керек.

856. интенгралын табу керек

Шешуі:

857. интегралын табу керек.

Шешуі:

Берілген интегралды табу керек.

858. Жауабы:

859. Жауабы:

860. Жауабы:

861. Жауабы:

862. Жауабы:

863. Жауабы:

864. Жауабы:

865. Жауабы:

Бақылау сұрақтары

1. Анықталмаған интегралдың анықтамасы.

2. Анықталмаған интегралдың қасиеттері.

3. Негізгі элементар функциялардың интегралдарының кестесі.

4. Анықталмаған интегралда айнымалыны алмастыру.

5. Анықталмаған интегралда бөліктеп интегралдау әдісі.

6. Қарапайым бөлшектерді интегралдау.

7. Рационал бөлшектерді интегралдау.

8. Иррационал бөлшектерді интегралдау.

9. Тригонометриялық функцияларды интегралдау.

10. Тригонометриялық қойылым.

8 Анықталған интеграл

8.1 Анықталған интегралды есептеу

Анықталған интегралдың анықтамасы. функциясының аралығындағы анықталған интегралы деп

интегралдық қосындының шегін айтады және былай белгілейді:

мұндағы а - төменгі, - жоғарғы шегі, – айнымалы шама, –интегралдау аралығы.

Егер функциясы аралығында үзіліссіз болса, онда осы аралықта интегралданады.

А н ы қ т а л ғ а н и н т е г р а л қ а с и е т т е р і:

1) Анықталған интеграл функциясының түріне және интегралдың шектеріне байланысты болады, бірақ интегралдау айнымалысына байланысты болмайды. Сондықтан оны әртүрлі әріппен белгілеуге болады, яғни

;

2) Функциялардың алгебралық қосындысының анықталған интегралы олардың анықталған интегралдарының алгебралық қосындысына тең болады, яғни

;

3) Тұрақты көбейткішті интеграл таңбасының алдына шығаруға болады, яғни

;

4) Егер сегментінде теңсіздігі орындалса, онда

Салдар. Егер сегментінде теңсіздігі орындалса, онда

5) егер -де болса, онда

6)  Егер функциясы сегментінде үзіліссіз болса, онда

теңдігі орындалатындай осы аралықтан ең болмаса бір нүктесі табылады.

7)  Егер , онда ;    

8) ;

9)

Анықталған интегралды анықталмаған интеграл көмегімен есептеу.

Ж о ғ а р ғ ы ш е г і а й н ы м а л ы а н ы қ т а л ғ а н и н т е г р а л. Егер функциясы аралығында үзіліссіз болса, онда

функциясы функциясының алғашқы функциясы болады, яғни

Н ь ю т о н – Л е й б н и ц ф о р м у л а с ы. Егер болса, онда

алғашқы функциясы анықталмаған интегралын шешу арқылы есептеледі.

866. интегралын есептеу керек.

Шешуі:

867. интегралын есептеу керек.

Шешуі:

Берілген интегралдарды есептеу керек.

868. Жауабы:

869. Жауабы:

870. Жауабы:

871. Жауабы:

872. 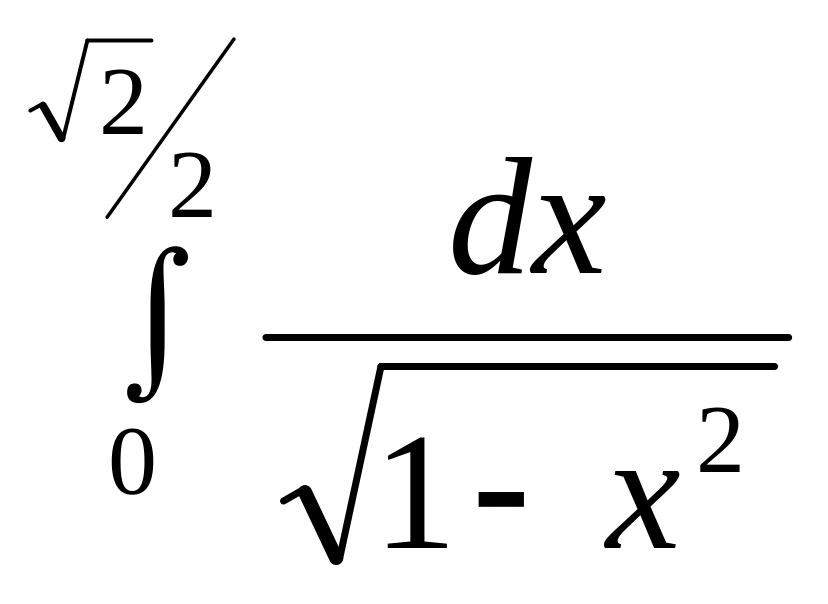Жауабы:

873. Жауабы:

874. Жауабы:

875. Жауабы:

876. Жауабы:

877. Жауабы:

878. Жауабы:

879. Жауабы:

880. Жауабы:

881. Жауабы:

882. Жауабы:

883. Жауабы:

884. Жауабы:

885. Жауабы: